Généralités
Les valeurs limites pour la déformation apparente des composants en béton armé sont prédéfinies par les conditions de section fissurée et non fissurée. RF-CONCRETE Deflect permet d’analyser les déformations en tenant compte de l’état de fissuration de la section. Les rigidités efficaces dans les éléments finis en fonction des conditions de section existantes sont calculées. Ces rigidités effectives sont par la suite utilisées dans les calculs aux éléments finis relatifs aux éléments surfaciques. Les rigidités efficaces sont contrôlées par le coefficient de distribution ζ, qui sera expliqué plus en détail dans ce qui suit.
Utilisation du coefficient de distribution ζ dans l’analyse des déformations
Le coefficient de déformation ζ est aussi appelé « facteur d’endommagement » ou « facteur de fissuration » dans la littérature spécialisée. L’utilisation du coefficient de déformation ζ dans l’analyse des déformations est spécifiée dans l’Équation 7.18 de l’EN 1992-1-1 [1].
La variable a représente le paramètre de flèche analysé (par exemple, la courbure). aI et aII sont les valeurs du paramètre calculées respectivement dans l'état non fissuré et dans l'état fissuré. L'équation montre que ζ = 0 prévaudra pour l'état de la section non fissurée (état I).
Si l’on utilise la courbure de la section (voir la formule 2) pour le paramètre de flèche générale a, on obtient une approche pour la détermination de la rigidité de la section efficace.
Détermination du coefficient de distribution ζ
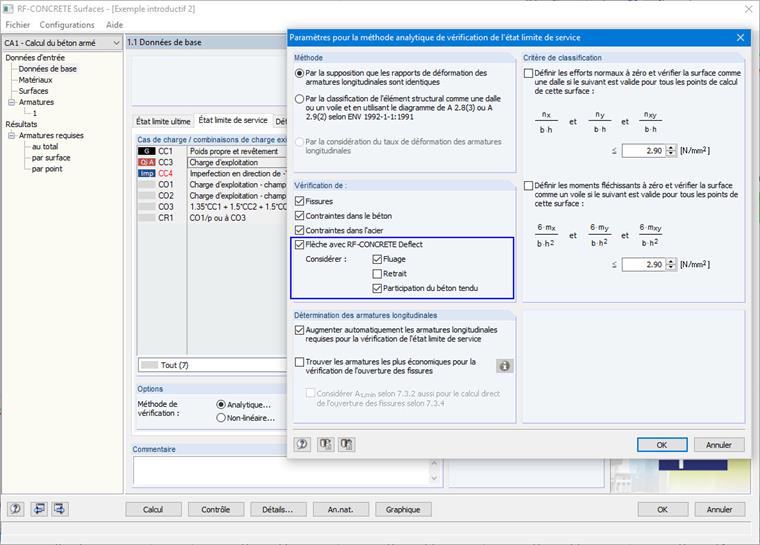
Le coefficient de distribution ζ est un indicateur dans l'analyse des déformations qui montre si une section est fissurée ou non. De plus, le coefficient ζ considère l'interaction du béton entre les fissures (raidissement en traction). L'application d'un raidisseur en traction peut être contrôlée dans les paramètres de RF-CONCRETE Deflect (voir la Figure 01). C'est pourquoi ces deux situations (avec et sans prise en compte des raidisseurs entre les fissures) seront examinées dans la suite de cet article.
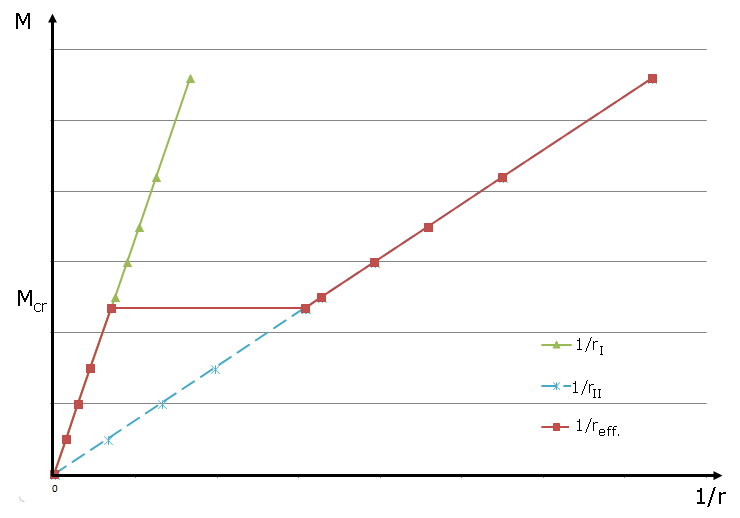
Si l'interaction du béton entre les fissures n'est pas appliquée dans l'analyse des déformations, le coefficient de distribution n'a que deux valeurs. ζ est égal à 0 dans le cas d'une section non fissurée et à 1 dans le cas d'une section fissurée. Ce paramètre se reflète clairement sur le diagramme moment-courbure correspondant. La courbure reste à l'état I dans le cas d'une charge avec le moment de fissuration Mcr. La courbure pour les sections entièrement fissurées s'applique lorsque le moment de fissuration est dépassé.
Si l'approche du raidissement en traction est utilisée dans le calcul de la déformation, le coefficient de distribution est compris entre 0 et 1. Pour une charge supérieure aux efforts internes de fissuration, le coefficient de distribution est déterminé selon les spécifications de la norme de calcul respective. Il est calculé comme suit dans RF-CONCRETE Deflect lors de l’analyse des déformations effectuée selon l’EN 1992-1-1 [1].
|
β |
Paramètres de l'influence de la durée du chargement ou de la répétition du chargement |
|
fctm |
résistance moyenne en traction du béton |
|
σmax |
Contrainte de traction du béton en faisant l'hypothèse d'un comportement de matériau linéaire-élastique |
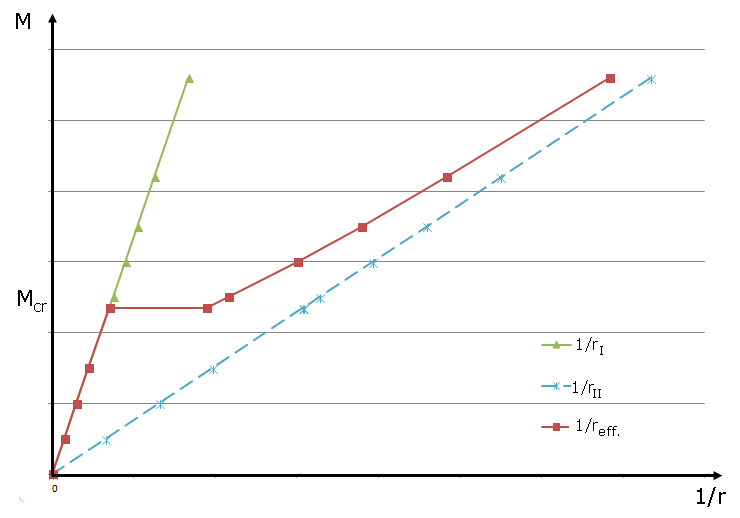
L'influence du raidissement en traction sur la déformation moyenne ou la courbure moyenne est flagrante sur le diagramme moment-courbure de la Figure 03. Lorsqu'elle est chargée, la courbure efficace est supérieure aux efforts internes de la fissure entre les zones non fissurée et fissurée et se rapproche continuellement de l'état fissuré avec une charge plus élevée.
Conclusion
Le diagramme moment-courbure figurant dans cet article montre que l'approche selon le raidissement en traction exerce un impact notable sur la détermination du coefficient de distribution ζ et donc sur la courbure moyenne et la déformation moyenne. L'ingénieur doit décider, en fonction de la tâche a réaliser, s'il faut appliquer ou non la capacité de charge selon l'interaction du béton entre les fissures lors de l'analyse des déformations. Il est prudent de ne pas considérer l'effet de raidissement en traction, comme le montre la Figure 02, car l'état de la section complètement fissurée est utilisé pour l'analyse des déformations lorsque les efforts internes de la fissure sont dépassés.
..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)
.png?mw=350&hash=206da82a5edbab18e7feb9cce3ac14ee719cdfdd)
.png?mw=512&hash=4a84cbc5b1eacf1afb4217e8e43c5cb50ed8d827)
_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)
-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
