Obecně
Mezní hodnoty deformace železobetonových dílců jsou předem stanoveny pro průřez bez trhlin a s trhlinami. Modul RF-CONCRETE Deflect umožňuje při posouzení deformace uvážit stav průřezu s trhlinami. S ohledem na daný stav průřezu se vypočítají hodnoty účinné tuhosti v konečných prvcích. Tyto hodnoty účinné tuhosti se následně použijí u plošných prvků při výpočtu metodou konečných prvků. Účinnou tuhost ovlivňuje rozdělovací součinitel ζ, kterým se budeme podrobněji zabývat níže.
Uplatnění rozdělovacího součinitele ζ při výpočtu deformace
Rozdělovací součinitel ζ lze najít v odborné literatuře také pod názvem součinitel vzniku trhlin nebo součinitel poškození. Použití rozdělovacího součinitele ζ při výpočtu deformace upřesňuje rovnice 7.18 v normě EN 1992-1-1 [1].
Proměnná a přitom představuje uvažovanou přetvárnou veličinu (například křivost). aI a aII jsou hodnoty parametru vypočteného pro stav bez trhlin a s plně rozvinutými trhlinami. Z rovnice vyplývá, že pro ζ = 0 je rozhodující stav průřezu bez trhlin (stav I).
Pokud jako obecnou přetvárnou veličinu a použijeme zakřivení průřezu
, získáme výraz pro stanovení účinné tuhosti průřezu.
Stanovení rozdělovacího součinitele ζ
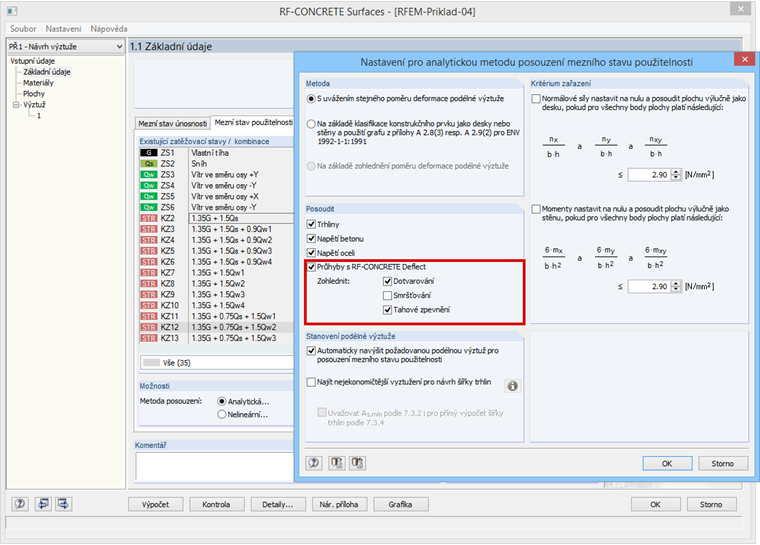
Rozdělovací součinitel ζ je při výpočtu deformace v modulu RF-CONCRETE Deflect ukazatelem, zda je průřez neporušený anebo porušený trhlinami. Dále součinitel ζ zohledňuje spolupůsobení betonu mezi trhlinami, takzvané tahové zpevnění průřezu. Možnost zohlednit tahové zpevnění se nám nabízí v nastavení modulu RF-CONCRETE Deflect (viz obr. 01). Následně se proto podíváme na obě situace, tj. na případ, kdy se tahové zpevnění průřezu mezi trhlinami uvažuje, i na případ, kdy se naopak neuvažuje.
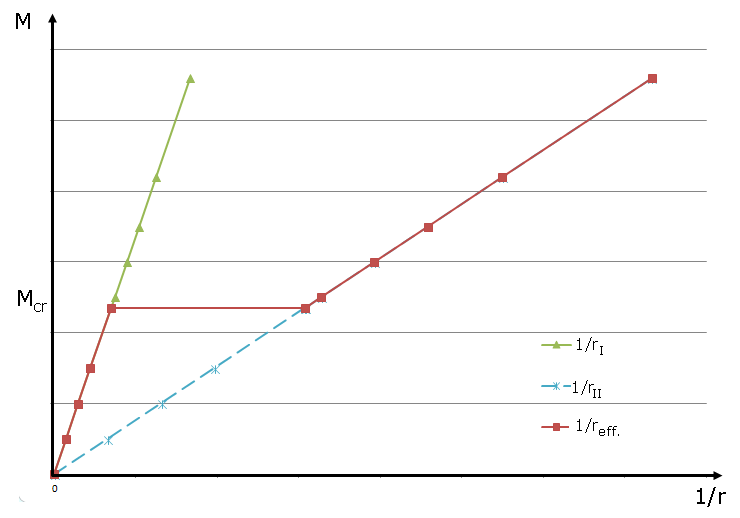
Pokud tahové zpevnění průřezu při výpočtu deformace nezohledňujeme, pak může mít rozdělovací součinitel pouze dvě hodnoty. V případě průřezu bez trhlin se ζ rovná 0 a u průřezu porušeného trhlinami má tento součinitel hodnotu 1. Jaký je výsledný vliv, můžeme dobře vidět v příslušném diagramu pro vyjádření vztahu mezi momentem a zakřivením. Při zatížení momentem Mcr na mezi vzniku trhlin zůstává zakřivení ve stavu I. Při překročení momentu na mezi vzniku trhlin je zakřivení rozhodující pro průřez s plně rozvinutými trhlinami.
Pokud při výpočtu deformace zohledňujeme tahové zpevnění, pak se rozdělovací součinitel nachází v rozmezí hodnot 0 a 1. Při zatížení, které přesáhne moment na mezi vzniku trhlin, se rozdělovací součinitel stanoví v souladu s příslušnou návrhovou normou. V případě výpočtu deformace podle EN 1992-1-1 [1] se součinitel vypočítá v modulu RF-CONCRETE Deflect následovně:
kde
β = součinitel, kterým se zohledňuje vliv doby trvání nebo opakování zatížení na průměrnou hodnotu poměrného přetvoření
fctm = průměrná hodnota pevnosti betonu v tahu
σmax = napětí betonu v tahu za předpokladu lineárně pružného chování materiálu
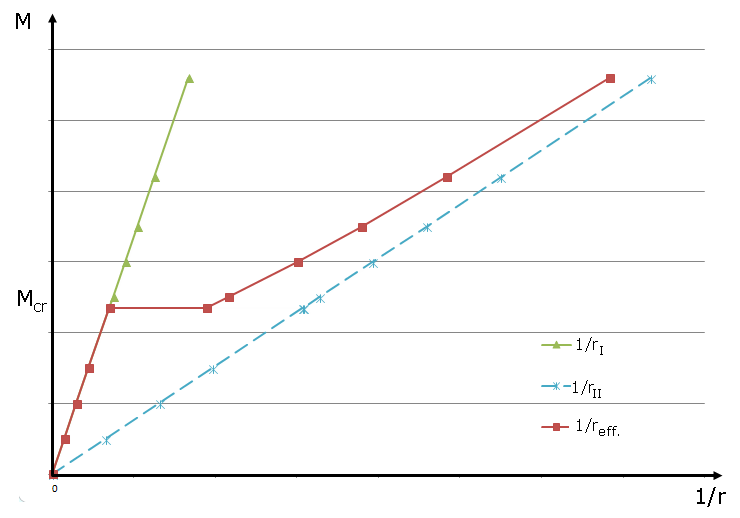
Vliv tahového zpevnění na průměrné přetvoření, respektive zakřivení je dobře zřetelný v diagramu vztahu mezi momentem a zakřivením na obr. 03. Účinné zakřivení se při zatížení nad momentem na mezi vzniku trhlin nachází v mezilehlém stavu mezi stavem bez trhlin a stavem s plně rozvinutými trhlinami a se stoupajícím zatížením se stále více blíží stavu s plně rozvinutými trhlinami.
Závěr
Ze znázorněných diagramů pro vyjádření vztahu mezi momentem a zakřivením je zřejmé, že zohlednění tahového zpevnění má podstatný vliv na stanovení rozdělovacího součinitele ζ, a tím také na průměrné zakřivení, respektive přetvoření. V závislosti na konkrétní úloze je na uvážení statika, zda při výpočtu deformace zohlední rezervu v únosnosti plynoucí ze spolupůsobení betonu mezi trhlinami. Jak je zřejmé z obr. 02, nezohlednění tahového zpevnění je na straně bezpečnosti, neboť při překročení momentu na mezi vzniku trhlin se pro výpočet deformace použije průřez s plně rozvinutými trhlinami.
