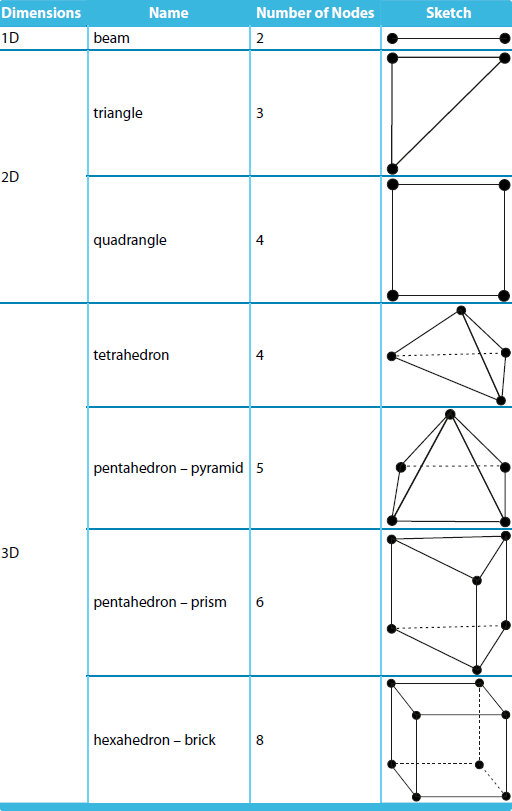
下表列出了 RFEM 中使用的有限元单元类型。 They are chosen automatically by the program according to the situation.
板件类型
- 1D beam element: Element with rotational degrees of freedom
- 2D plate element: Lynn–Dhillon; MITC3; MITC4 – used in case of nonlinear calculation
- 2D wall element: With stabilized zero energy modes
- 2D shell element: Shell element = plate element + wall element
- 3D solid element: Element with rotational degrees of freedom; element without rotational degrees of freedom (with or without extra shape functions), gas element, contact element
Integration Procedure
For members, analytical integration is used for linear cases, while in the nonlinear setting the two point Gauss quadrature is used along the beam. For nonlinear cases, the following integration rule is used in the cross-section: 2×2 Gauss quadrature for quadrangles and 4-point selective reduced integration rule for triangles (3 points for 𝜖x, 𝜖y and 1 point for 𝛾xy).
In plate elements, analytical integration is used whenever possible (in Lynn–Dhillon element or in a triangular element). In other cases, a 2×2 composite Gauss quadrature is used in the element plane (quadrangles). In solids, a 2×2×2 composite Gauss quadrature is used in hexahedrons. Reduced one point integration is used for some particular terms to avoid numerical problems.
Let us focus on integration in plates with respect to their thickness, which is based on the Gauss–Lobatto quadrature. The Gauss–Lobatto quadrature is a Gauss quadrature in which boundary points are forced to also be integration points, which allows an exact evaluation of stresses on layer interfaces in case of multilayered plates. In case of linear calculation, three integration points are used per layer. In nonlinear calculation, nine integration points are used in the plate (nonlinear calculation allows one layer only).