连接刚度对杆件和连接节点设计的影响

本文解释了在支座区域中所选模型对内力和变形的影响。

模型描述A-E

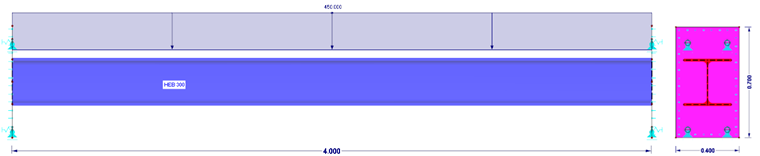
模型A表示使用纯杆件模型的标准情况。 梁的两侧都是刚性的，所有六个自由度都被锁定。 该模型没有非线性。 杆件模型由“刚性”类型的节点支座支撑。

模型A.

在模型B中，杆件的两端都有一个刚性的端板，该端板是线性支撑的。 刚性表示不考虑板的变形。 该支座建模为纯面支座。

B模型。

在模型C中，杆件的两端都有一个刚性的端板，该端板是非线性支撑的。 在面支座中只吸收压应力。 剪力和拉力被非线性定义的节点支座吸收。

模型C.

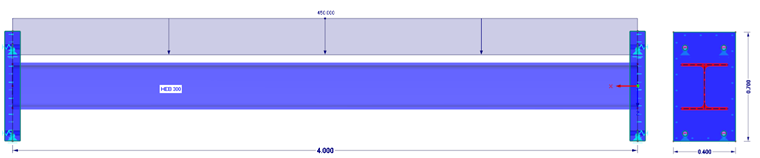
在模型D中，杆件的两端都有一个有限的厚端板（t = 100 mm），并且是非线性支撑的。 在面支座中只吸收压应力。 剪力和拉力被非线性定义的节点支座吸收。

模型D.

在模型E中，杆件的两端都有一个有限厚的端板（t = 40 mm），并且是非线性支撑的。 在面支座中只吸收压应力。 剪力和拉力被非线性定义的节点支座吸收。

E型

“销钉”建模注意事项： 在我们的示例中，模型C，模型D和模型E包含非线性平移弹簧，以传递拉力。

结果评估和比较

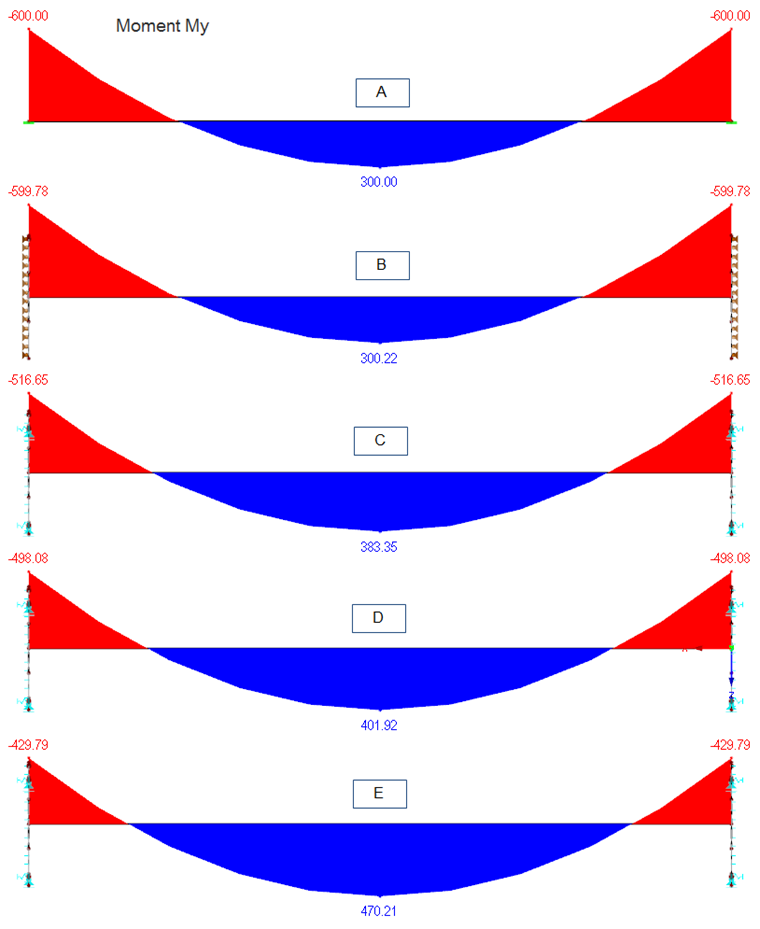
简单的杆件模型（模型A）在刚度约束中表现出最大的弯矩，因此在跨度中最小。 关于端板和紧固件的设计，这是最保守的结果。 但是，跨度中的弯矩被低估了。

模型B的结果与模型A几乎相同。 带有线性支座的刚性面不考虑其他结果。 这种建模在实践中是不合理的。

与简单杆件模型相比，在模型C中非线性计算表明跨距中的弯矩明显增加了27％。 约束力矩相应减小。

支座条件越真实，跨距中的弯矩越大。 因此，模型D中的弯矩比简单杆件模型高大约34％。

当使用钢板的实际厚度时，支座条件的影响最大。 如模型E所示，在这种情况下，空间中的弯矩增加了56％。

内力My

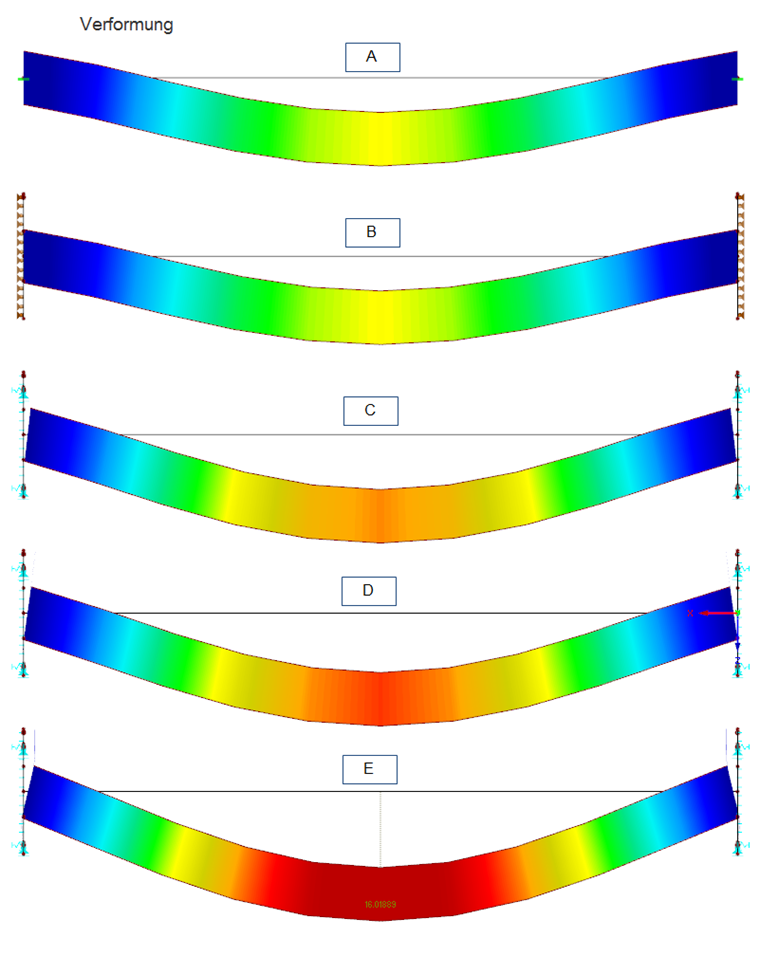
变形也是重要的边界条件。 这些图清楚地表明了各个模型对梁的变形有何影响。 在模型A和模型B中，约束位置完全不变形。 在这里，跨度变形很小。 相反，在模型E中，由于高荷载作用，实际钢板厚度为40 mm时会出现明显的板变形。 在这种情况下，板的实际刚度对梁变形的影响特别明显。

应该注意的是，在这个简化的例子中没有考虑材料的非线性（塑性）。 当然，在端板中达到屈服强度后会发生较大的变形。

warp

小结

根据不同的任务和目标，使用有限元方法模拟接近真实的支座条件。 这可以在RFEM中快速有效地完成，RFEM提供了各种有用的工具，并且可以直观的输入。 因此可以更好地评估在支座作用下构件的结构性能。

此外，这种详细的连接设计可以精确评估施加到其他结构构件上的荷载。 因此，工程师可以在满足高安全性标准的同时提供高效可行的解决方案。

在重新计算现有的构件或紧固件时，支座条件的有限元建模也非常有用。例如由于他们的转换。 在极限范围内移动越多，实际建模的工作量就越合理。