Влияние жесткости соединений на расчет стержней и соединений

В данной статье описывается влияние выбранной модели в зоне опоры на внутренние силы и деформации.

Описание моделей A - E

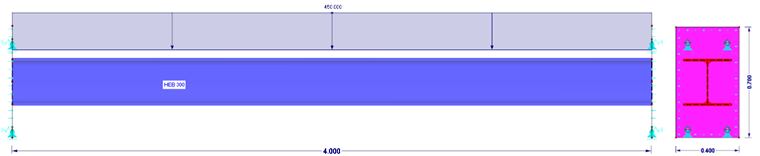
Модель A представляет собой стандартный случай использования чистой модели стержня. Балка жесткая с обеих сторон, все шесть степеней свободы заблокированы. Модель не имеет нелинейностей. Модель стержня поддерживается узловыми опорами типа «Жесткий».

Модель А.

В модели B стержень с обеих сторон имеет жесткую концевую пластину, которая поддерживается линейно. Жесткость означает, что деформации пластины не учитываются. Опора моделируется как опора для чистой поверхности.

Модель B.

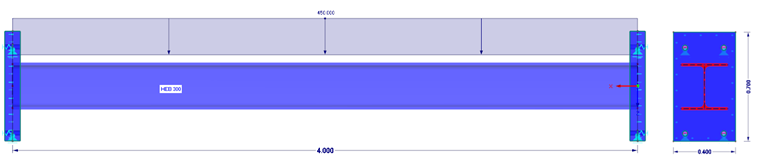
В модели C стержень с обеих сторон имеет жесткую концевую пластину, которая поддерживается нелинейно. В опоре поверхности поглощаются только сжимающие напряжения. Поперечные и растягивающие силы поглощаются нелинейно заданными узловыми опорами.

Модель C.

В модели D стержень имеет конечную толстую торцевую пластину (t = 100 мм) с обеих сторон, которая поддерживается нелинейно. В опоре поверхности поглощаются только сжимающие напряжения. Поперечные и растягивающие силы поглощаются нелинейно заданными узловыми опорами.

Модель D.

В модели E стержень с обеих сторон имеет конечную толстую торцевую пластину (t = 40 мм), которая имеет нелинейную опору. В опоре поверхности поглощаются только сжимающие напряжения. Поперечные и растягивающие силы поглощаются нелинейно заданными узловыми опорами.

Модель E.

Примечание для моделирования 'дюбелей': В нашем примере модель C, модель D и модель E включают в себя нелинейную поступательную пружину для передачи растягивающих сил.

Оценка и сравнение результатов

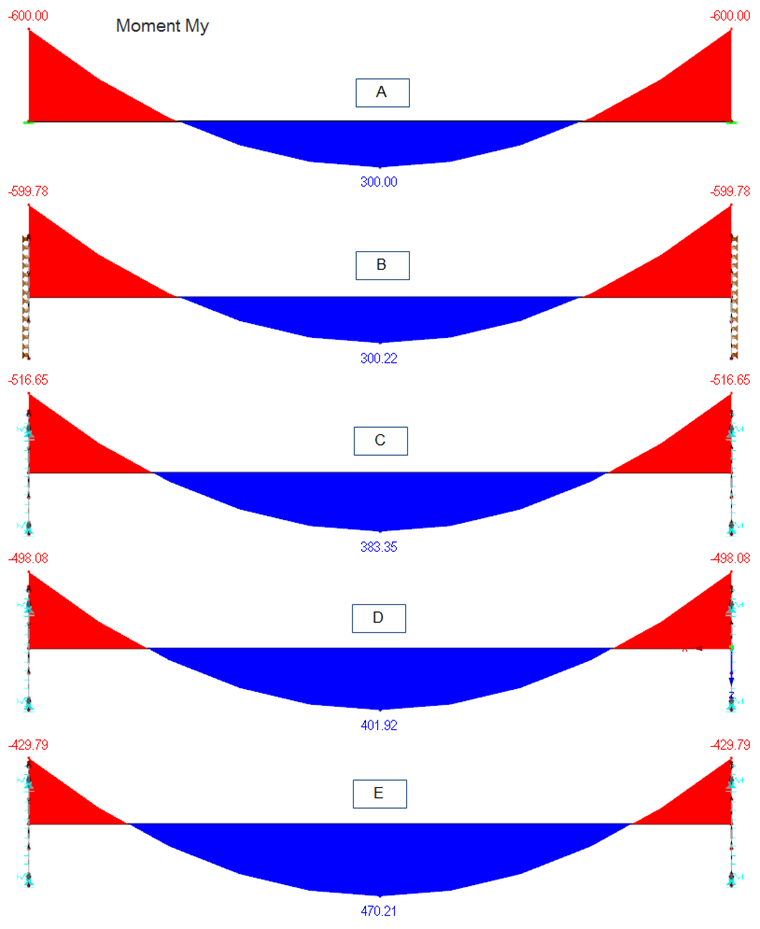
Простая модель стержня (модель A) с жестким ограничением показывает, как и ожидалось, самые большие удерживающие моменты и, следовательно, самый низкий момент в пролете. Что касается конструкции концевой плиты и крепежа, то это наиболее консервативный результат. Однако момент в пролете недооценен.

Модель B показывает почти те же результаты, что и модель A. Жесткая поверхность с линейной опорой не дает никаких других результатов. Такое моделирование на практике нецелесообразно.

В модели C нелинейность показывает явное увеличение момента в пролете на 27% по сравнению с простой моделью стержня. Удерживающий момент соответственно уменьшается.

Чем реалистичнее условия опоры, тем больше увеличивается момент в пролете. Таким образом, момент в пролете примерно на 34% выше в модели D, чем в простой модели стержня.

Влияние условий опоры является наиболее значительным при использовании реальной толщины стальной пластины. В этом случае, момент в пространстве увеличивается на 56%, как видно из модели E.

Внутренняя сила My

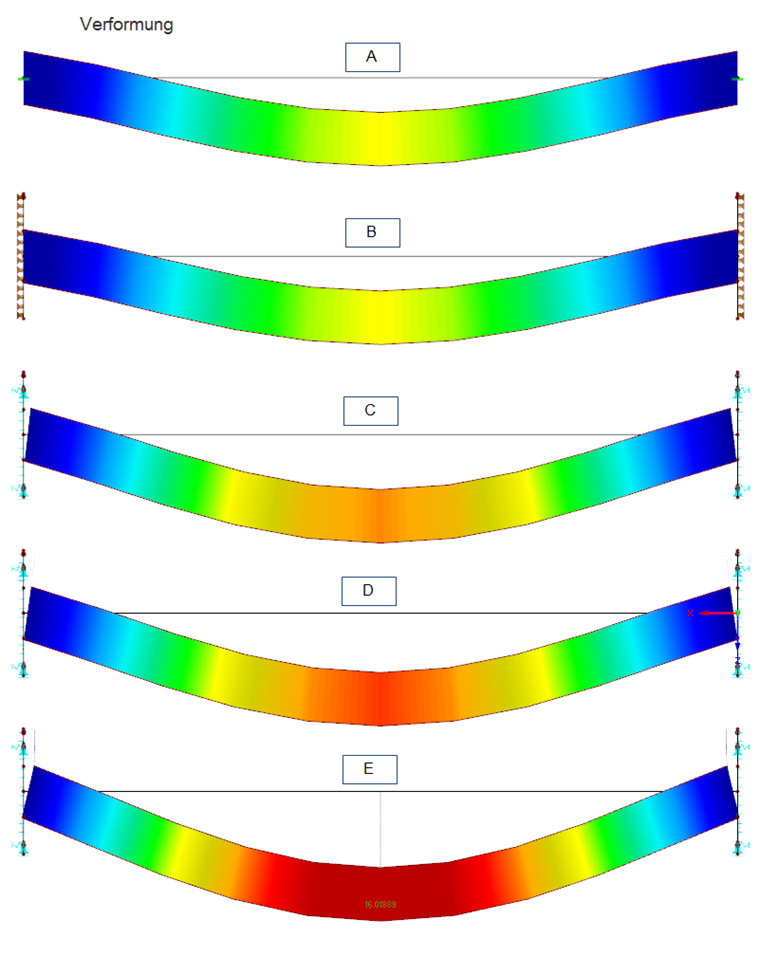
Деформации также являются важными граничными условиями. На рисунках четко показано, какое влияние оказывает соответствующее моделирование на деформацию балки. В моделях A и B, место удержания остается полностью не деформированным. Здесь деформации пролета малы. В отличие от этого, в модели E возникают значительные деформации пластин с реальной толщиной стальной пластины 40 мм из-за высокой нагрузки. В этом случае влияние реальной жесткости пластины на деформацию балки особенно очевидно.

Следует отметить, что нелинейность материала (пластичность) в данном упрощенном примере не учитывается. Разумеется, после достижения предела текучести в концевых пластинах могут возникнуть большие деформации.

основа

Заключение

В зависимости от поставленных задач и задач, может быть целесообразно смоделировать условия опирания, близкие к реальности, с помощью метода конечных элементов. Это можно сделать быстро и эффективно в программе RFEM, которая предоставляет различные полезные инструменты и обеспечивает интуитивный ввод данных. Таким образом, можно лучше оценить конструктивное поведение компонентов под воздействием опор.

Кроме того, этот подробный расчет соединения позволяет точно оценить приложение нагрузки к другим конструктивным элементам. Таким образом, инженер может предложить эффективные и выполнимые решения, при этом отвечая высоким стандартам безопасности.

Моделирование условий опирания по МКЭ также может быть полезно при пересчете существующих компонентов или крепежных элементов; например, из -за их преобразования. Чем больше вы будете двигаться в определенных пределах, тем более разумным будет усилие реалистичного моделирования.