Cet article explique l'influence du modèle sélectionné dans la zone d'appui sur les efforts internes et les déformations.
Description des modèles A - E
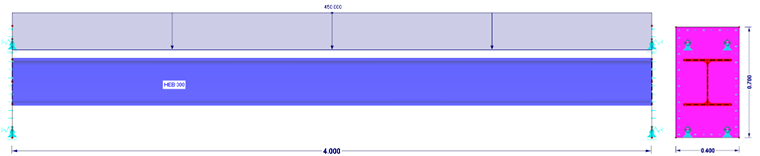
Le modèle A représente le cas standard d'utilisation d'un modèle de barre pure. La poutre est rigide des deux côtés et les six degrés de liberté sont bloqués. Le modèle n'a pas de non-linéarités. Le modèle de barre est supporté par des appuis nodaux de type «Rigide».
Dans le modèle B, la barre est dotée d'une platine d'extrémité rigide des deux côtés, qui est supportée linéairement. Rigide signifie que les déformations de la plaque ne sont pas prises en compte. L'appui est modélisé comme un appui de surface pur.
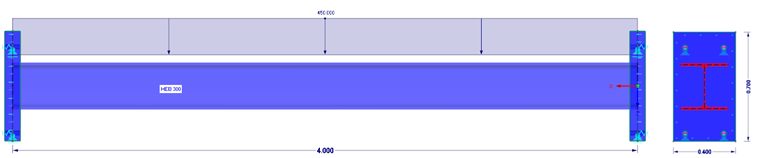
Dans le modèle C, la barre est dotée d'une platine d'extrémité rigide des deux côtés, qui est supportée de manière non linéaire. Seules les contraintes de compression sont absorbées dans le support de surface. Les efforts tranchants et de traction sont absorbés par des appuis nodaux définis de manière non linéaire.
Dans le modèle D, la barre a une platine d'extrémité finie (t = 100 mm) épaisse des deux côtés, qui est supportée de manière non linéaire. Seules les contraintes de compression sont absorbées dans le support de surface. Les efforts tranchants et de traction sont absorbés par des appuis nodaux définis de manière non linéaire.
Dans le modèle E, la barre a une platine d'extrémité finie (t = 40 mm) d'épaisseur qui est supportée de manière non linéaire. Seules les contraintes de compression sont absorbées dans le support de surface. Les efforts tranchants et de traction sont absorbés par des appuis nodaux définis de manière non linéaire.
Remarque pour la modélisation des «chevilles»: Dans notre exemple, les modèles C, D et E incluent un ressort de translation non linéaire afin de transférer les efforts de traction.
Évaluation et comparaison des résultats
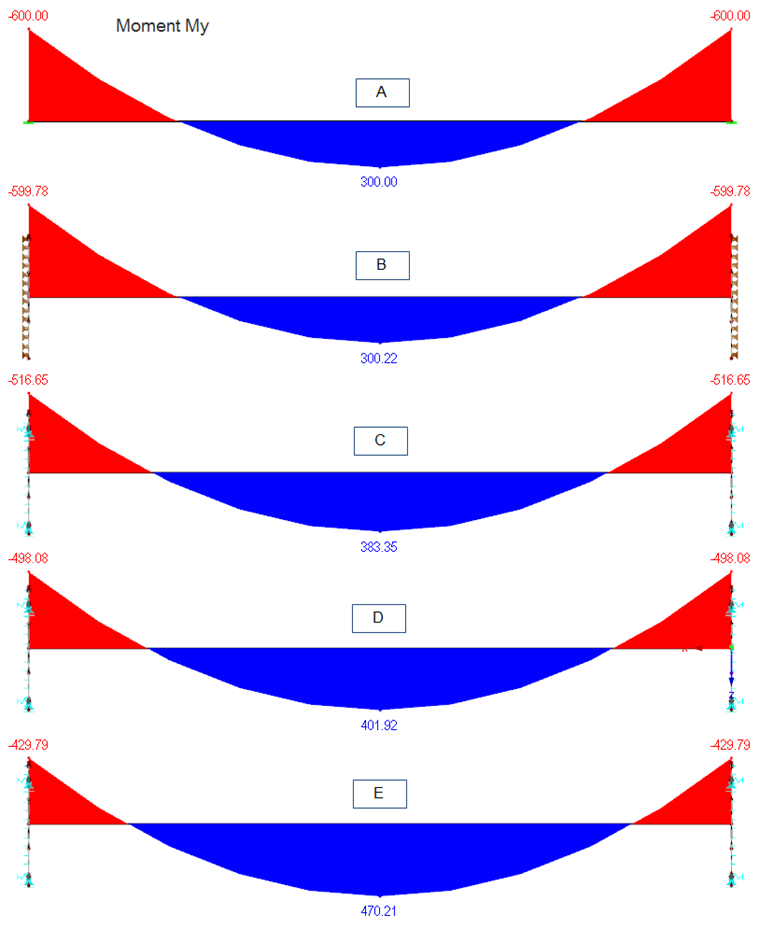
Le modèle de barre simple (modèle A) avec contrainte rigide affiche, comme prévu, les moments de retenue les plus importants et donc le moment le plus bas de la travée. Il s’agit du résultat le plus conservateur en ce qui concerne le calcul de la platine et de la fixation. Cependant, ce moment est sous-évalué.
Le modèle B donne presque les mêmes résultats que le modèle A. La surface rigide avec appui linéaire ne permet pas d'autres résultats. Une telle modélisation n'est pas raisonnable en pratique.
Dans le modèle C, la non-linéarité affiche une augmentation nette du moment de la travée de 27% par rapport au modèle de barre simple. Le moment de retenue diminue en conséquence.
Plus les conditions d'appui sont réalistes, plus le moment dans la travée augmente. Ainsi, le moment dans la travée est environ 34% plus élevé dans le modèle D que dans le modèle à barre simple.
L'influence des conditions d'appui est la plus importante lors de l'utilisation de l'épaisseur réelle de la plaque d'acier. Le moment dans l'espace est augmenté de 56% dans ce cas, comme le montre le modèle E.
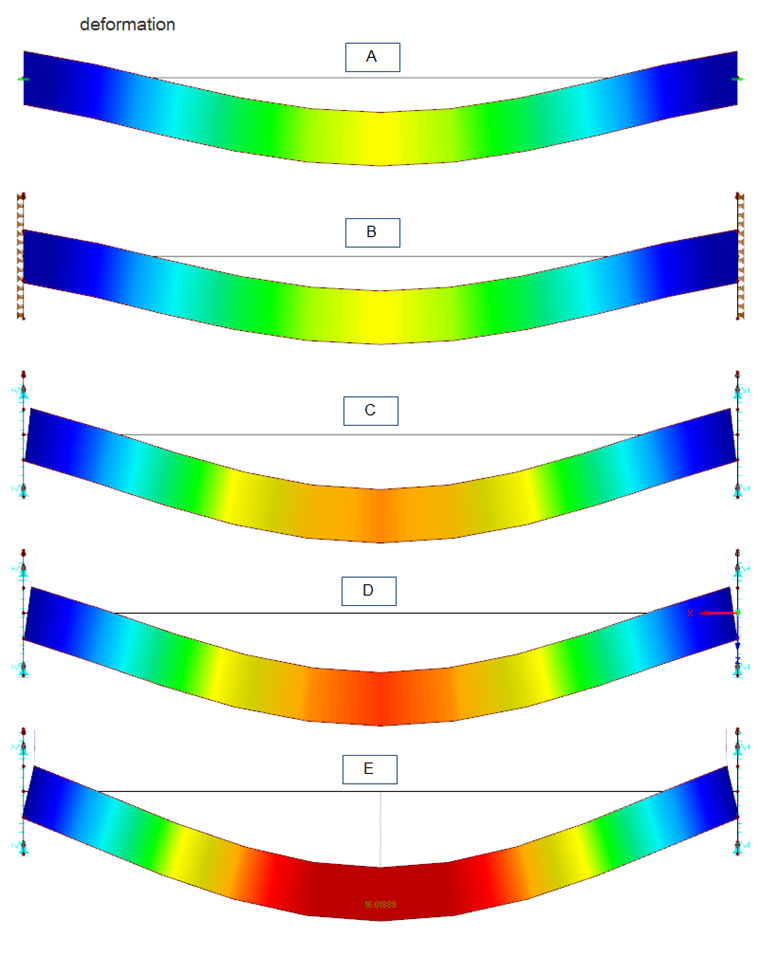
Les déformations sont également des conditions aux limites importantes. Les figures montrent clairement l'influence de la modélisation respective sur la déformation de la poutre. Dans les modèles A et B, l'emplacement des dispositifs de retenue reste complètement non déformé. Les déformations de portée sont ici faibles. En revanche, le modèle E présente des déformations importantes de la plaque avec une épaisseur réelle de plaque de 40 mm en raison de la charge élevée. Dans ce cas, l'influence de la rigidité réelle de la plaque sur la déformation de la poutre est particulièrement claire.
Il convient de noter que la non-linéarité du matériau (plasticité) n'est pas considérée dans cet exemple simplifié. Bien entendu, des déformations plus importantes peuvent survenir après avoir atteint la limite d'élasticité dans les platines d'about.
Résumé
Selon les tâches et les objectifs, il peut être raisonnable de modéliser les conditions d'appui proches de la réalité à l'aide de la méthode des éléments finis. Cette opération peut être effectuée rapidement et efficacement dans RFEM, qui fournit divers outils utiles et permet une saisie intuitive. Ainsi, vous pouvez mieux évaluer le comportement structural des composants sous l'influence des appuis.
De plus, cette connexion détaillée permet d'évaluer avec précision la charge appliquée à d'autres composants structuraux. Ainsi, un ingénieur peut fournir des solutions efficaces et réalisables tout en respectant un standard de sécurité élevé.
La modélisation aux éléments finis des conditions d'appui peut également être utile lors du recalcul des composants ou des fixations existants; par exemple, à cause de leur conversion. Plus vous vous déplacez dans les limites limites, plus les efforts déployés par la modélisation réaliste sont raisonnables.