W artykule wyjaśniono wpływ wybranego modelu w obszarze podparcia na siły wewnętrzne i odkształcenia.
Opis modeli A - E
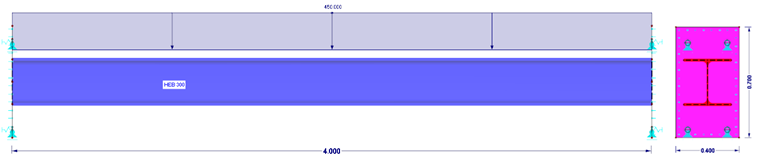
Model A stanowi standardowy przypadek zastosowania modelu czysto prętowego. Dźwigar jest po obu stronach sztywny, wszystkie sześć stopni swobody jest zablokowanych. Model nie ma nieliniowości. Model pręta jest podparty przez podpory węzłowe typu „Sztywne”.
W Modelu B pręt posiada po obu stronach sztywną płytę końcową, która jest podparta liniowo. Sztywna oznacza, że odkształcenia płyty nie są uwzględniane. Podpora jest modelowana jako czysta podpora powierzchniowa.
W Modelu C pręt posiada po obu stronach sztywną płytę końcową, która jest podparta nieliniowo. W podporze powierzchniowej przenoszone są tylko naprężenia ściskające. Siły tnące i rozciągające są przenoszone przez nieliniowo zdefiniowane podpory węzłowe.
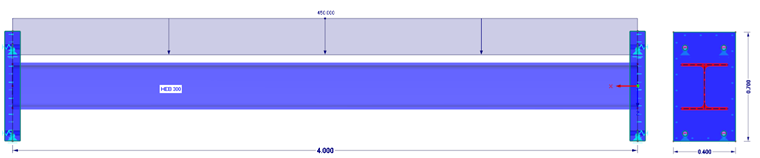
W Modelu D pręt posiada po obu stronach po obu stronach podłużną blachę czołową (t = 100 mm), która jest podparta nieliniowo. W podporze powierzchniowej przenoszone są tylko naprężenia ściskające. Siły tnące i rozciągające są przenoszone przez nieliniowo zdefiniowane podpory węzłowe.
W Modelu E pręt ma po obu stronach skończoną, grubą płytę czołową (t = 40 mm), która jest podparta nieliniowo. W podporze powierzchniowej przenoszone są tylko naprężenia ściskające. Siły tnące i rozciągające są przenoszone przez nieliniowo zdefiniowane podpory węzłowe.
Uwaga do modelowania „kołków”: W naszym przykładzie, Model C, Model D i Model E zawierają nieliniową sprężynę translacyjną w celu przeniesienia sił rozciągających.
Ocena i porównanie wyników
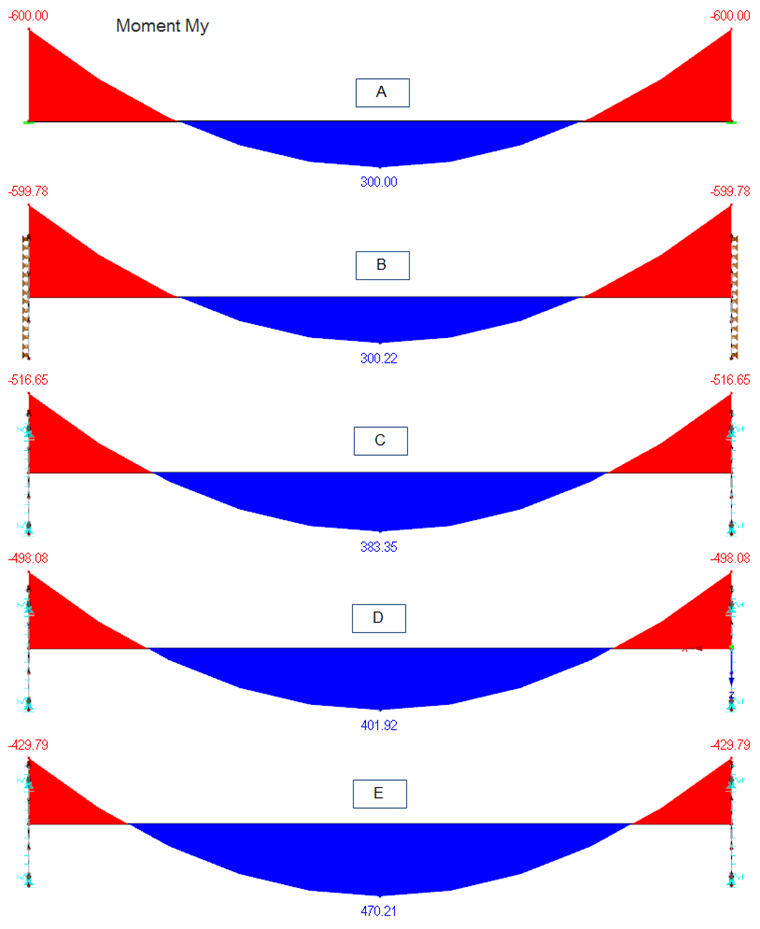
Prosty model prętowy (Model A) ze sztywnym utwierdzeniem pokazuje, zgodnie z oczekiwaniami, największe momenty ograniczające, a tym samym najmniejszy moment w przęśle. Jeśli chodzi o konstrukcję płyty końcowej i łącznika, jest to najbardziej konserwatywny wynik. Moment w przęśle jest jednak niedoceniany.
Model B wykazuje niemal takie same wyniki jak model A. Sztywna powierzchnia z podpórą liniową nie pozwala na inne wyniki. Takie modelowanie nie jest w praktyce racjonalne.
W Modelu C nieliniowość pokazuje wyraźny wzrost momentu w przęśle o 27% w porównaniu z prostym modelem prętowym. Moment ograniczający zmniejsza się odpowiednio.
Im bardziej realistyczne są warunki podparcia, tym bardziej zwiększa się moment w przęśle. Dzięki temu moment w przęśle jest o około 34% większy w modelu D niż w prostym modelu prętowym.
Wpływ warunków podparcia jest najbardziej znaczący w przypadku zastosowania rzeczywistej grubości stalowej płyty. W tym przypadku moment w przestrzeni zostaje zwiększony o 56%, jak widać w modelu E.
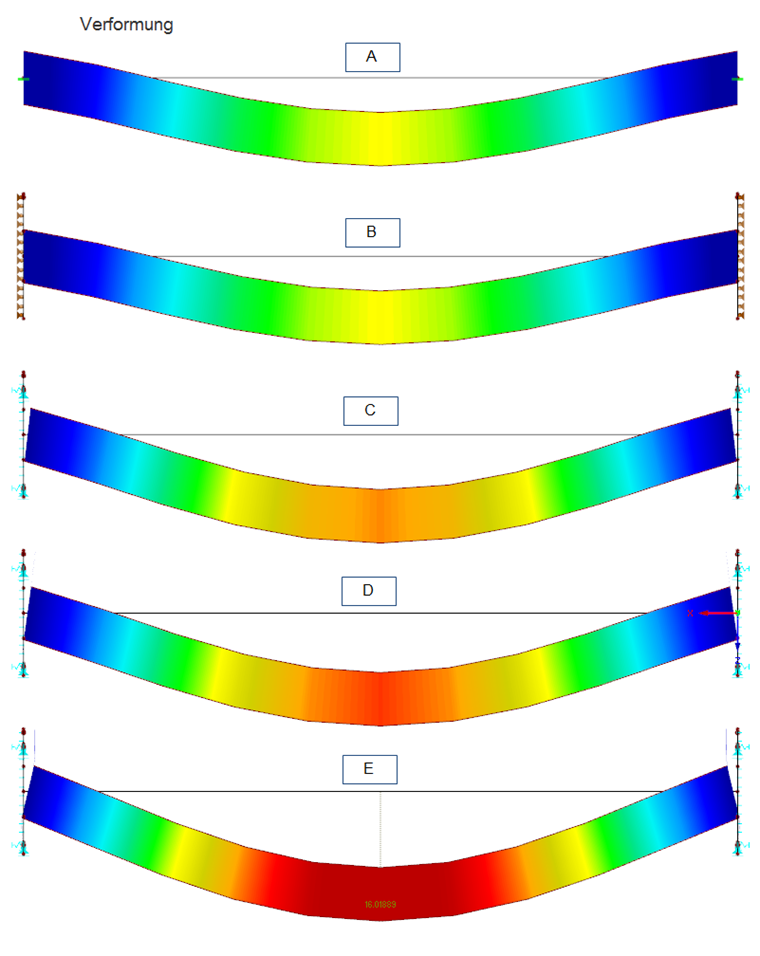
Odkształcenia są również ważnymi warunkami brzegowymi. Na rysunkach wyraźnie widać, jaki wpływ ma modelowanie na odkształcenie dźwigara. W modelach A i modelu B położenie utwierdzenia pozostaje całkowicie niezkształcone. W tym przypadku odkształcenia rozpiętości są niewielkie. Natomiast w modelu E występują znaczne odkształcenia płyty przy rzeczywistej grubości płyty stalowej 40 mm z powodu dużego obciążenia. W tym przypadku szczególnie wyraźny jest wpływ rzeczywistej sztywności płyty na odkształcenie dźwigara.
Należy zauważyć, że w tym uproszczonym przykładzie nie uwzględniono nieliniowości materiałowej (plastyczności). Oczywiście po osiągnięciu granicy plastyczności w płytach końcowych mogą wystąpić większe odkształcenia.
Podsumowanie
W zależności od zadań i celów może być uzasadnione zamodelowanie warunków podparcia w sposób zbliżony do rzeczywistości przy użyciu Metody Elementów Skończonych. Można to zrobić szybko i efektywnie w programie RFEM, który oferuje różne przydatne narzędzia i umożliwia intuicyjne wprowadzanie danych. Pozwala to na lepszą ocenę zachowania konstrukcyjnego elementów pod wpływem podpór.
Ponadto, ten szczegółowy projekt połączenia umożliwia dokładną ocenę przyłożenia obciążenia na inne elementy konstrukcyjne. Dzięki temu inżynier może dostarczyć efektywne i możliwe do rozwiązania rozwiązanie, spełniając jednocześnie wysokie normy bezpieczeństwa.
Modelowanie MES warunków podparcia może być również przydatne podczas przeliczania istniejących elementów lub łączników; na przykład ze względu na ich konwersję. Im więcej poruszasz się w określonych granicach, tym bardziej realistyczny jest model.