Vliv tuhosti přípoje na posouzení prutů a spojů

V našem příspěvku si předvedeme, jaký vliv má zvolený model v oblasti podpor na vnitřní síly a deformace.

Popis modelů A - E

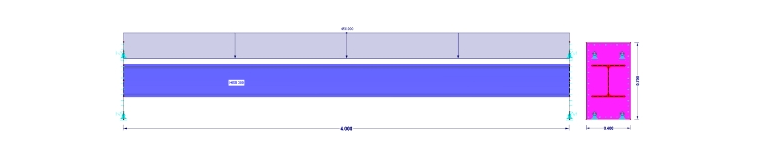
Model A představuje standardní řešení v případě čistě prutového modelu. Nosník je na obou stranách plně vetknutý, všech šest stupňů volnosti bylo odebráno. Model nevykazuje žádné nelinearity. Prutový model je podepřen uzlovými podporami typu „Vetknutí“.

Model A

V modelu B je prut na obou stranách opatřen lineárně podepřenou tuhou čelní deskou. U tuhé čelní desky se přitom deformace neuvažují. Podepření modelujeme jako čistě plošnou podporu.

Model B

V modelu C má prut na obou stranách nelineárně podepřenou tuhou čelní desku. Plošná podpora přenáší pouze napětí v tlaku. Posouvající a tahové síly přenášejí uzlové podpory, u nichž rovněž zadáme nelinearitu.

Model C

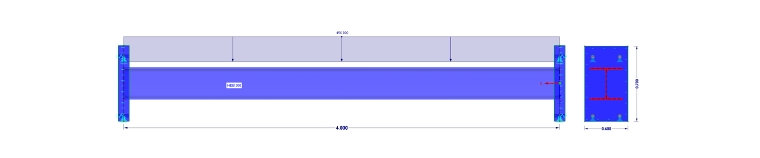
U modelu D je prut na obou stranách opatřen čelní deskou s konečnou tloušťkou (t = 100 mm) a nelineárním podepřením. Plošná podpora přenáší pouze napětí v tlaku. Posouvající a tahové síly přenášejí nelineární uzlové podpory.

Model D

U modelu E má prut na obou stranách čelní desku s konečnou tloušťkou (t = 40 mm) a nelineárním podepřením. Plošná podpora přenáší pouze napětí v tlaku. Posouvající a tahové síly přenášejí nelineární uzlové podpory.

Model E

Poznámka k modelování „kolíků“: u modelů C až E jsme zadali nelineární translační pružinu pro přenos tahových sil.

Vyhodnocení a porovnání výsledků

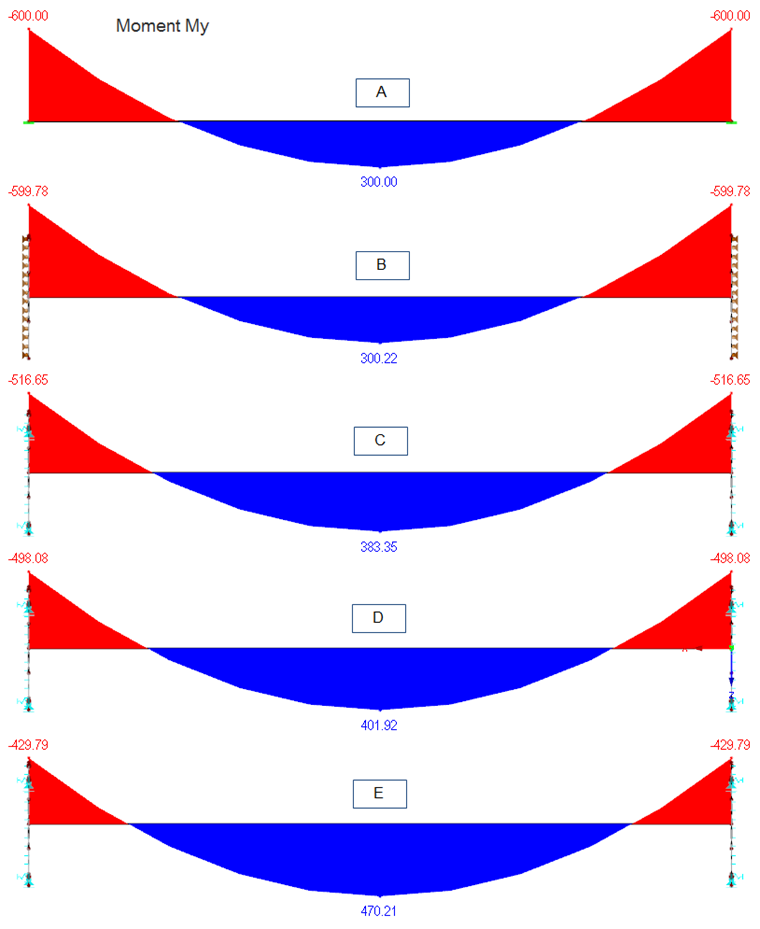
Jednoduchý prutový model (model A) s tuhým vetknutím vykazuje podle očekávání největší momenty ve vetknutí, a tudíž i nejmenší moment v poli. Pokud jde o dimenzování čelní desky a spojovacích prostředků, jedná se o nejkonzervativnější řešení. Moment v poli je ovšem podhodnocen.

Model B vykazuje téměř stejné výsledky jako model A. U tuhé plochy s lineárním podepřením ani nelze očekávat jiné výsledky. Tento způsob modelování nemá v praxi opodstatnění.

U modelu C s definovanou nelinearitou můžeme pozorovat výrazný nárůst momentu v poli o 27 % v porovnání s prostým prutovým modelem. Moment ve vetknutí se odpovídajícím způsobem sníží.

Čím realističtěji modelujeme podporové podmínky, tím více roste moment v poli. Zvýšení tohoto momentu dosahuje u modelu D již 34 % oproti jednoduchému prutovému modelu.

Nejvýrazněji se projevuje vliv podporových podmínek při zvolení reálné tloušťky ocelové desky. U modelu E tak lze zaznamenat o 56 % větší moment v poli.

Vnitřní síly My

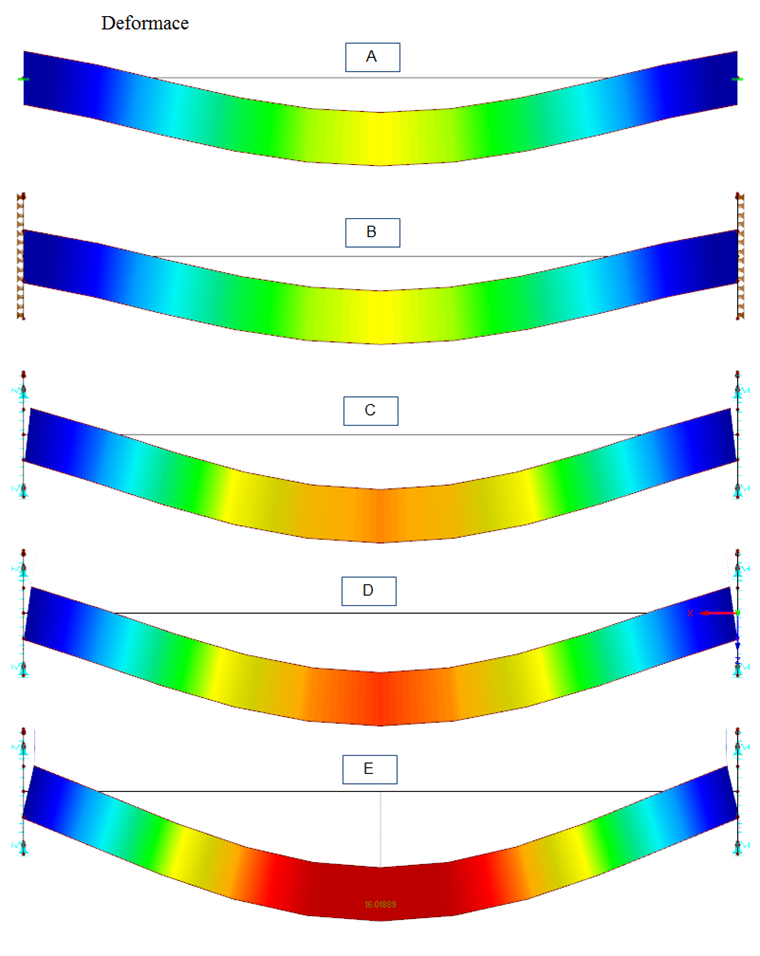
Deformace představují rovněž důležité mezní podmínky. Z obrázků je zřejmé, jaký vliv bude mít daný způsob modelování na deformaci nosníku. U modelů A a B nevznikají v místě vetknutí žádné deformace. Deformace pole jsou malé. Oproti tomu v modelu E s reálnou tloušťkou ocelové desky 40 mm dochází vlivem vysokého zatížení k výrazným deformacím desky. V tomto případě je vliv reálné tuhosti desky na deformace nosníku obzvlášť zřetelný.

Je třeba poznamenat, že v našem jednoduchém příkladu se materiálová nelinearita (plasticita) neuvažuje. Po dosažení meze kluzu v čelních deskách by bylo samozřejmě možné pozorovat opět jiné/větší deformace.

Deformace

Závěr

V závislosti na projektovém zadání může být vhodné modelovat podporové podmínky realisticky metodou konečných prvků. Program RFEM se svými užitečnými funkcemi a intuitivním zadáváním vstupních dat přitom nabízí rychlé a efektivní řešení. Chování nosných konstrukčních prvků při konkrétních podporových podmínkách tak lze lépe vyhodnotit.

Detailně řešený návrh přípojů umožňuje také přesně zhodnotit přenos zatížení do jiných konstrukčních dílců. Lze tak vypracovat hospodárná a proveditelná řešení, která přesto splňují vysoké bezpečnostní standardy.

Modelování podporových podmínek metodou MKP lze doporučit také v případě, že potřebujeme přepočítat stávající konstrukční prvky nebo spoje například kvůli změně jejich využití. Čím více nás omezují limity, tím více se nám vyplatí realistický způsob modelování.