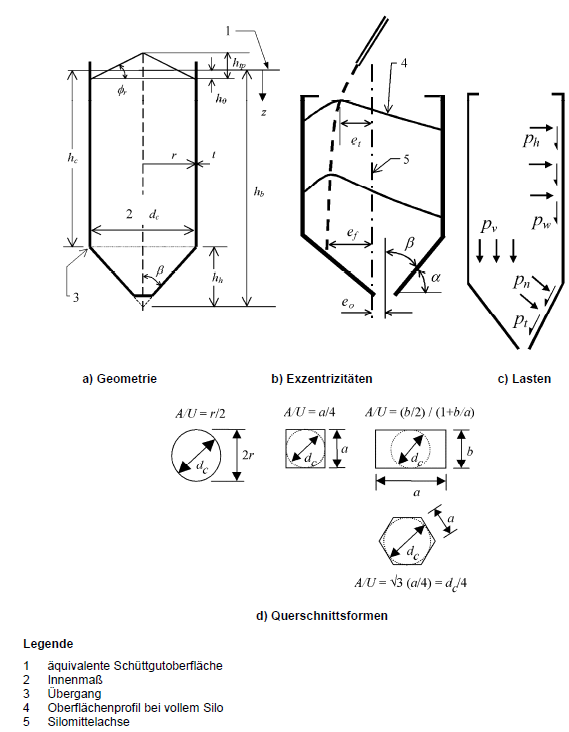
Champ d'application
L'application des règles de calcul pour les silos et les réservoirs est soumise à des limitations géométriques. In DIN EN 1991-4 [1] sind die geometrischen Abmessungen auf hb / dc < 10 mit hb < 100 m sowie dc < 60 m beschränkt. Darüber hinaus werden Anwendungsgrenzen hinsichtlich der Querschnittsform des Silos und des gelagerten Schüttguts genannt.
Schüttgutkennwerte
Der Anhang E der DIN EN 1991-4 [1] gibt Kennwerte für die gängigsten in Silos gelagerten Schüttgüter an, die der Streuung in den Schüttguteigenschaften Rechnung tragen. Darüber hinaus werden in Abschnitt 4 und Anhang C der DIN EN 1991-4 [1] Angaben über die experimentelle Ermittlung von Schüttgutkennwerten gemacht.
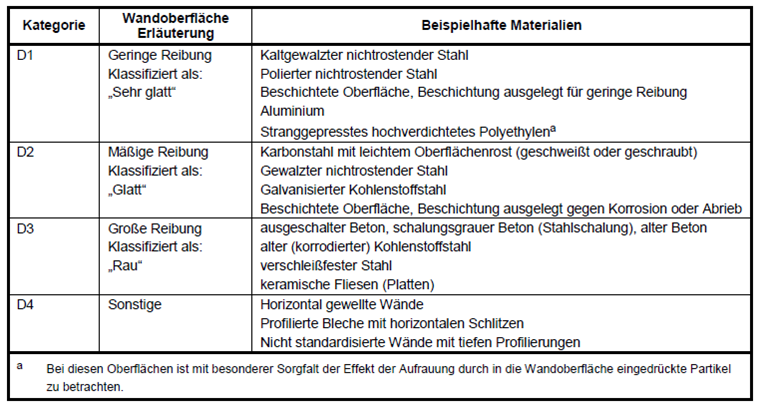
Die Wandreibungsbeiwerte von Schüttgütern berücksichtigen die Rauheit der Wandoberflächen, an welchen sie entlang gleiten. In Tabelle 4.1 der DIN EN 1991-4 [1] sind unterschiedliche Kategorien von Wandoberflächen definiert. Die Kategorien der Wandoberflächen sind in der nachstehenden Tabelle dargestellt. Im Anhang D.2 der DIN EN 1991-4 [1] werden darüber hinaus Angaben zur Abschätzung des effektiven Wandreibungskoeffizienten für die Kategorie D4 gemacht.
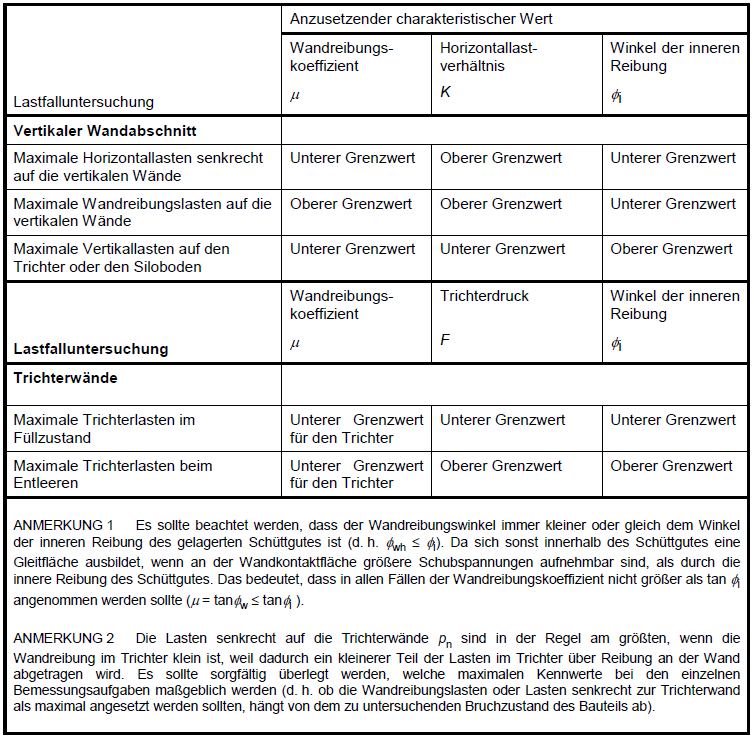
Die Ermittlung der Lasten eines Lastfalles hat immer für eine bestimmte Kombination von zusammengehörigen Schüttgutkennwerten zu erfolgen. Für jeden dieser Lastfälle werden seine Extremwerte erreicht, wenn die Schüttgutkennwerte jeweils unterschiedliche Extremwerte innerhalb der Streubreiten ihrer charakteristischen Schüttgutkennwerte annehmen. Die zu verwendenden Extremwerte der Schüttgutkennwerte sind für jeden der zu untersuchenden Lastfälle in Tabelle 3.1 der DIN EN 1991-4 [1] angegeben. Die maßgeblichen Kennwerte für die unterschiedlichen Lastansätze sind der folgenden Tabelle zu entnehmen dargestellt.
Classe structurale
Silozellen werden in Abhängigkeit von ihrem Fassungsvermögen und der Exzentrizität gemäß Tabelle 2.1 der DIN EN 1991-4 [1] in drei Anforderungsklassen eingeteilt.
Entsprechend der jeweiligen Anforderungsklasse sind unterschiedlich differenzierte beziehungsweise vereinfachte Lastansätze anzunehmen.
Lasten auf vertikale Silowände
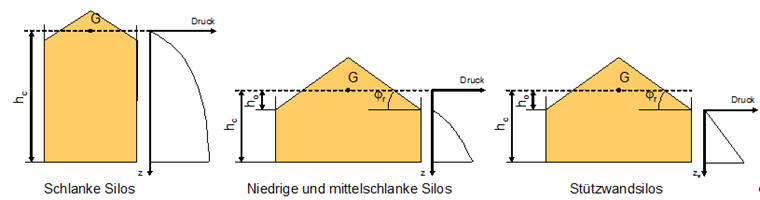
Die Lasten auf vertikale Silowände werden differenziert nach der Siloschlankheit berechnet. Es wird unterschieden zwischen:
schlanken Silos (hc / dc ≥ 2,0)
Silos mit mittlerer Schlankheit (1,0 < hc / dc < 2,0)
niedrigen Silos (0,4 < hc / dc ≤ 1,0) und
Stützwandsilos (hc / dc ≤ 0,4 und waagerechter Siloboden)
Symmetrische Lasten
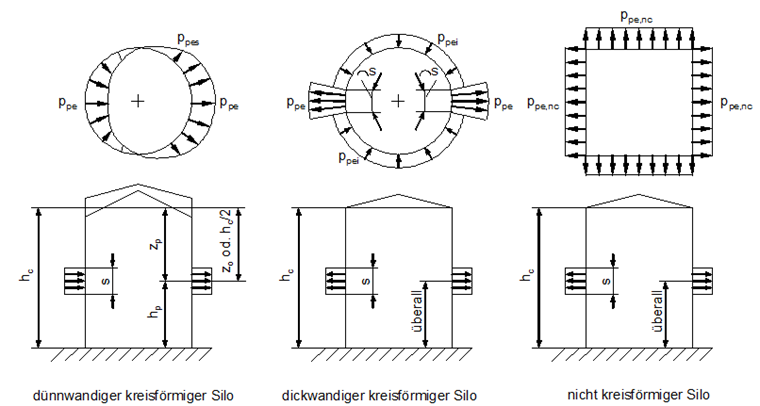
Die symmetrischen Lasten sind ortsfeste Lasten, die gleichmäßig über den Siloumfang verteilt sind. Die Entleerungslasten ergeben sich aus der Erhöhung der gleichmäßigen Lasten des Füllzustandes mit einem Lastvergrößerungsfaktor.
Unsymmetrische Lasten
Im Regelfall sind neben den ortsfesten Lasten zusätzliche freie Lasten anzusetzen. Unsymmetrische Lastverteilungen im Silo werden zum Beispiel durch Einflüsse infolge Imperfektionen oder Exzentrizitäten beim Füllen und Entleeren hervorgerufen.
Die Teilflächenlast ist bei dickwandigen kreisförmigen Silos auf eine quadratische Teilfläche mit der Seitenlänge s an entgegen gesetzten Seiten anzusetzen. Bei nichtkreisförmigen Silos können die Teilflächenlasten durch eine Erhöhung der symmetrischen Lasten berücksichtigt werden. Die nach außen gerichtete Teilflächenlast ist dabei als streifenförmiges Lastband mit der Bandbreite s anzusetzen.
Der Ansatz von Teilflächenlasten ist bei niedrigen Silos und Silos mit mittlerer Schlankheiten nicht generell erforderlich.
Bei Silos der Anforderungsklasse 2 darf das Verfahren der Teilflächenlasten näherungsweise durch eine gleichmäßige Erhöhung der Horizontallasten ersetzt werden.
Lasten beim Entleeren mit großen Exzentrizitäten
Die DIN EN 1991-4 [1] sieht Lasten infolge großer Entleerungsexzentrizitäten als separaten Lastfall vor. Der Entwicklung dieses Lastansatzes liegt die Vorstellung zugrunde, dass sich infolge des stark exzentrischen Entleerens ein Fließkanal in der Nähe der Wand ausbildet. Es wird von einem kreisförmigen Fließkanal ausgegangen, der über die Höhe der Silowand als konstant angenommen wird und die Silowand unter einem Öffnungswinkel θc schneidet.
Eine theoretische Vorhersage der sich einstellenden geometrischen Form der Entleerungstrombe ist mit den heute zur Verfügung stehenden Hilfsmitteln kaum möglich, so dass daher im Regelfall der Fließkanal vorgegeben werden muss. Die Berechnung ist mit mindesten drei verschiedenen Fließkanalradien rc durchzuführen, um die sich einstellende Variationen des Fließkanals erfassen zu können.
In den Kontaktbereichen des fließenden Schüttguts mit der Silowand treten geringere Horizontaldrücke auf als außerhalb des Fließkanals. Im letzteren Bereich werden die Lasten des Lastfalls Füllen angesetzt. Unmittelbar neben dem Fließkanal bis zu einem Öffnungswinkel von 2 θc werden Druckerhöhungen aufgebracht.
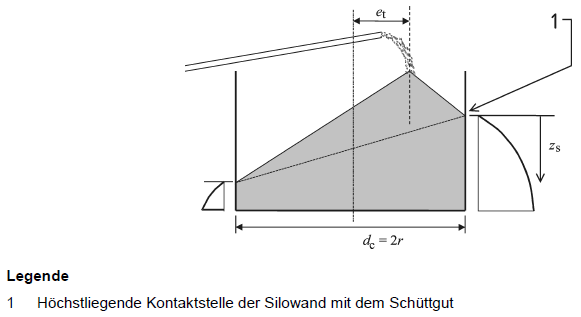
Große Exzentrizitäten beim Befüllen
Lasten infolge exzentrischen Befüllens sind bei niedrigen Silos und Silos mittlerer Schlankheit zu berücksichtigen.
In DIN EN 1991-4 [1] sind zusätzliche vertikale Wandlasten in einer Tiefe zs unterhalb des höchstliegenden Berührungspunktes des Schüttgutes mit der Wand zu bestimmen. Dieser Lastanteil ist mit den bis zur Schüttguttiefe z aufsummierten Wandreibungslasten zu überlagern.
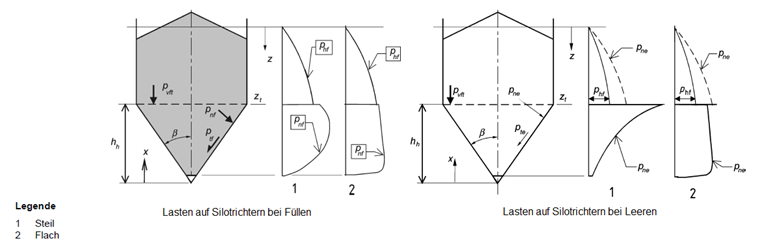
Lasten auf Silotrichter und Siloböden
Die Lasten auf die Wände von Silotrichtern sind unter Berücksichtigung der Neigung der Trichterwände nach EN 1991-4 [1] zu ermitteln.
Die Norm unterscheidet zwischen ebenen Böden sowie steil und flach geneigten Trichtern. In steilen Trichtern wird zusätzlich zwischen dem Lastfall Füllen und Entleeren unterschieden. Die Lastspitze am Übergang vom Siloschaft zum Trichter ist in den Lastansätzen bereits enthalten.
Im Anhang G der EN 1991-4 [1] sind alternative Regeln zur Ermittlung von Trichterlasten enthalten.
Exemple
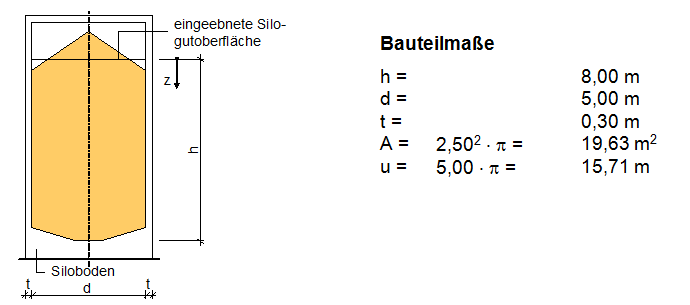
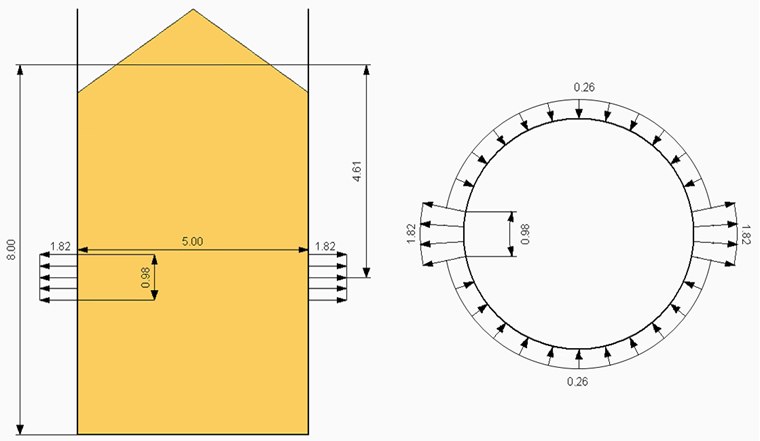
Das Beispiel umfasst einen freistehenden zylindrischen Silo für Zement mit 5,00 m Durchmesser und einer größten Schüttguttiefe von 8,00 m. Das Silo wird in Stahlbeton mit einer Wanddicke von 0,30 m hergestellt.
Schüttgut
Die folgenden Schüttgutkennwerte wurden der Tabelle E.1 der DIN EN 1991-4 [1] für das Schüttgut Zement entnommen.
- Wichte (oberer Wert) γu = 16,00 kN/m3
- Böschungswinkel Φr = 36,00°
- Winkel der inneren Reibung (Mittelwert) Φim = 30,00°
- Umrechnungsfaktor aφ = 1,22
- Horizontallastverhältnis (Mittelwert) Κm = 0,54
- Umrechnungsfaktor aΚ = 1,20
- Wandreibungskoeffizient (Wandtyp D3) μm = 0,51 (für Beton)
- Umrechnungsfaktor aμ = 1,07
- Kennwert für Teilflächenlast Cop = 0,50
Charakteristische Schüttgutkennwerte
Zur Ermittlung der charakteristischen Kennwerte des Horizontallastverhältnisses, des Wandreibungskoeffizienten und des Winkels der inneren Reibung sind die aufgelisteten Mittelwerte des Schüttguts mit Konversionsfaktoren zu skalieren. Die Umrechnungsfaktoren ax sind in der Tabelle E.1 1 für die dort aufgeführten Schüttgüter angegeben.
Oberer und unterer charakteristischer Wert des Horizontallastverhältnisses
Κu = aΚ ∙ Κm = 1,20 ∙ 0,54 = 0,648
Κl = Κm / aΚ = 0,54 / 1,20 = 0,450
Oberer und unterer charakteristischer Wert des Wandreibungskoeffizienten
μu = aμ ∙ μm = 1,07 ∙ 0,51 = 0,546
μl = μm / aμ = 0,51 / 1,07 = 0,477
Oberer und unterer charakteristischer Wert des Winkels der inneren Reibung
Φiu = aΦ ∙ Φim = 1,22 ∙ 30,00° = 36,60°
Φil = Φim / aΦ = 30,00° / 1,22 = 24,59°
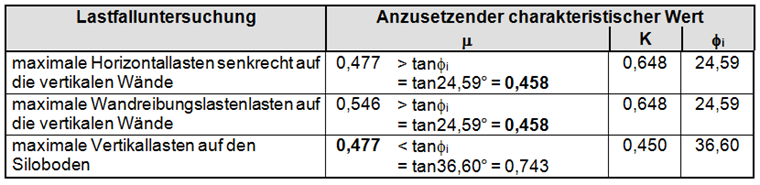
Maßgebliche Kennwerte für die unterschiedlichen Lastansätze
Die Ermittlung der Lasten eines Lastfalles hat immer für eine bestimmte Kombination von zusammengehörigen Schüttgutkennwerten zu erfolgen, so dass jedem Grenzzustand eine spezielle, definierte Beschaffenheit eines Schüttgutes zugeordnet ist. Die zu verwendenden Extremwerte der Schüttgutkennwerte sind für jeden der zu untersuchenden Lastfälle in der folgenden Tabelle angegeben.
Der Wandreibungswinkel muss immer kleiner oder gleich dem Winkel der inneren Reibung des gelagerten Schüttgutes sein, das heißt Φwh ≤ Φi. Ansonsten bildet sich innerhalb des Schüttgutes eine Gleitfläche aus, wenn an der Wandkontaktfläche größere Schubspannungen aufnehmbar sind als durch die innere Reibung des Schüttgutes selbst. Das bedeutet, dass in allen Fällen der Wandreibungskoeffizient nicht größer als tanΦi angenommen werden sollte (μ = tanΦw ≤ tanΦi). Das ist in der obenstehenden Tabelle berücksichtigt worden, die maßgebenden Werte sind fett hervorgehoben.
Actions
Die Ermittlung der Einwirkungen erfolgt auf der Grundlage der DIN EN 1991-4 [1]. Es sollen hier lediglich die Fülllasten auf vertikale Silowände sowie die Vertikallasten auf ebene Siloböden berechnet werden.
Klassifikation des Silos
Die Klassifikation des Silos erfolgt anhand der Schlankheit und der Anforderungsklasse.
Élancements
1,0 < hc / dc = 8,00 / 5,00 = 1,6 < 2,0
Das Silo ist gemäß 1.5.21 der DIN EN 1991-4 [1] als mittelschlank einzustufen.
Classe structurale
Fassung = V ∙ γu = 157,08 ∙ 16,00 = 2513,27 ≙ 2513,27 / 9,80665 = 256,28 t
Nach Tabelle 2.1 der DIN EN 1991-4 [1] ist mindestens die Anforderungsklasse 2 zu wählen.
Konstruktionsform
dc / t = 5,00 / 0,30 = 16,7 < 200
Das Silo ist gemäß 1.5.43 der DIN EN 1991-4 [1] als dickwandig einzustufen.
Symmetrische Fülllasten auf vertikale Silowände
charges horizontales
Charakteristische Tiefe zo nach der Theorie nach Janssen
Vertikaler Abstand ho
Der vertikale Abstand ho zwischen der äquivalenten Schüttgutoberfläche und der höchstgelegenen Kontaktstelle vom gespeicherten Schüttgut mit der Wand ist bei einem symmetrisch gefüllten kreisförmigen Silo anzunehmen mit:
Parameter n
Asymptotische Horizontallasten in großer Tiefe aus gespeichertem Schüttgut pho
pho = γ ∙ K ∙ zo = 16,00 ∙ 0,648 ∙ 4,22 = 43,70 kN/m² (5.73)
Horizontallasten phf(z)
- phf(0,61) = 0 kN/m²
- phf(1,61) = 13,26 kN/m²
- phf(2,61) = 20,93 kN/m²
- phf(3,61) = 25,83 kN/m²
- phf(4,61) = 29,19 kN/m²
- phf(5,61) = 31,62 kN/m²
- phf(6,61) = 33,43 kN/m²
- phf(7,61) =∙34,83 kN/m²
- phf(8,00) = 35,29 kN/m²
Wandreibungslasten
Charakteristische Tiefe zo nach der Theorie nach Janssen
Vertikaler Abstand ho
Der vertikale Abstand ho zwischen der äquivalenten Schüttgutoberfläche und der höchstgelegenen Kontaktstelle vom gespeicherten Schüttgut mit der Wand ist bei einem symmetrisch gefüllten kreisförmigen Silo anzunehmen mit:
Parameter n
Asymptotische Horizontallasten in großer Tiefe aus gespeichertem Schüttgut pho
pho= γ ∙ K ∙ zo = 16,00 ∙ 0,648 ∙ 4,22 = 43,70 kN/m² (5.73)
Wandreibungslasten pwf(z)
- pwf(0,61) = 0 kN/m²
- pwf(1,61) = 6,07 kN/m²
- pwf(2,61) = 9,58 kN/m²
- pwf(3,61) = 11,82 kN/m²
- pwf(4,61) = 13,36 kN/m²
- pwf(5,61) = 14,47 kN/m²
- pwf(6,61) = 15,30 kN/m²
- pwf(7,61) =∙15,94 kN/m²
- pwf(8,00) = 16,15 kN/m²
Vertikallasten
Charakteristische Tiefe zo nach der Theorie nach Janssen
Parameter n
Vertikallasten pvf(z)
- pvf(0,61) = 9,69 kN/m²
- pvf(1,61) = 23,65 kN/m²
- pvf(2,61) = 34,51 kN/m²
- pvf(3,61) = 43,27 kN/m²
- pvf(4,61) = 50,52 kN/m²
- pvf(5,61) = 56,65 kN/m²
- pvf(6,61) = 61,92 kN/m²
- pvf(7,61) = 66,50 kN/m²
- pvf(8,00) = 68,15 kN/m²
Vertikale Wandschnittkräfte nzSk(z)
- nzSk(z) = μ ∙ pho(z) ∙ (z - zv) (5.81)
- nzSk(0,61) = 0,00 kN/m
- nzSk(1,61) = 2,55 kN/m
- nzSk(2,61) = 8,97 kN/m
- nzSk(3,61) = 18,02 kN/m
- nzSk(4,61) = 28,96 kN/m
- nzSk(5,61) = 41,30 kN/m
- nzSk(6,61) = 54,72 kN/m
- nzSk(7,61) = 68,98 kN/m
- nzSk(8,00) = 74,81 kN/m
Unsymmetrische Fülllasten auf vertikale Silowände
Abmessung der mit Teilflächenlast belasteten Fläche
Charakteristische Tiefe zo nach der Theorie nach Janssen
Vertikaler Abstand ho
Der vertikale Abstand ho zwischen der äquivalenten Schüttgutoberfläche und der höchstgelegenen Kontaktstelle vom gespeicherten Schüttgut mit der Wand ist bei einem symmetrisch gefüllten kreisförmigen Silo anzunehmen mit:
Parameter n
Asymptotische Horizontallasten in großer Tiefe aus gespeichertem Schüttgut pho
pho = γ ∙ K ∙ zho = 16,00 ∙ 0,648 ∙ 4,22 = 43,70 kN/m² (5.73)
Lastvergrößerungsfaktor Cpf der Teilflächenlast beim Lastfall Füllen
Teilflächenlast für den Lastfall Füllen
- ppf(0,61) = 0 kN/m²
- ppf(1,61) = 0,83 kN/m²
- ppf(2,61) = 1,30 kN/m²
- ppf(3,61) = 1,61 kN/m²
- ppf(4,61) = 1,82 kN/m²
- ppf(5,61) = 1,97 kN/m²
- ppf(6,61) = 2,08 kN/m²
- ppf(7,61) = 2,17 kN/m²
- ppf(8,00) = 2,20 kN/m²
- ppfi(0,61) = 0 kN/m²
- ppfi(1,61) = 0,12 kN/m²
- ppfi(2,61) = 0,19 kN/m²
- ppfi(3,61) = 0,23 kN/m²
- ppfi(4,61) = 0,26 kN/m²
- ppfi(5,61) = 0,28 kN/m²
- ppfi(6,61) = 0,30 kN/m²
- ppfi(7,61) = 0,31 kN/m²
- ppfi(8,00) = 0,31 kN/m²
Lasten auf waagerechte Siloböden
Die Vertikallasten auf ebene Siloböden in Silos mit mittlerer Schlankheit können nicht mehr als konstant angenommen werden und berechnen sich aus den folgenden Lastansätzen:
Der Bodenlastvergrößerungsfaktor Cb ist bei Silos der Anforderungsklasse 2 unter der Voraussetzung angesetzt worden, dass das gelagerte Schüttgut beim Entleeren des Silos keine Tendenz zu dynamischem Verhalten aufweist.
Die Bodenlasten pvsq können sowohl für den Lastfall Füllen als auch für den Lastfall Entleeren angesetzt werden.
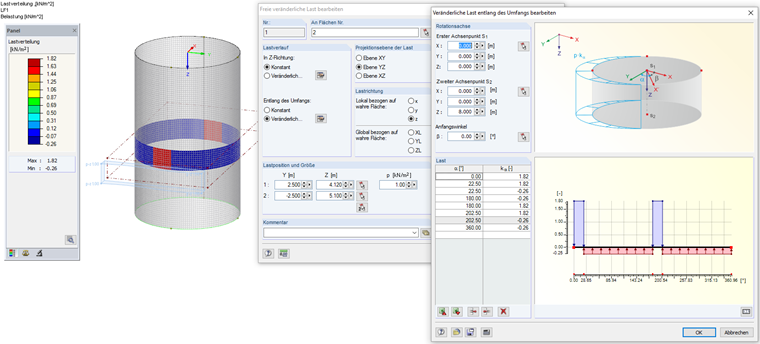
Eingabe der Lasten in RFEM
Die ermittelten Lasten können in RFEM eingegeben werden. Im Bild unten ist exemplarisch die Teilflächenlast für den Lastfall Füllen für z = 4,61 m dargestellt. Diese Last kann in RFEM als freie veränderliche Last eingegeben werden. Die Lasteingabe kann dem unteren Bild entnommen werden.