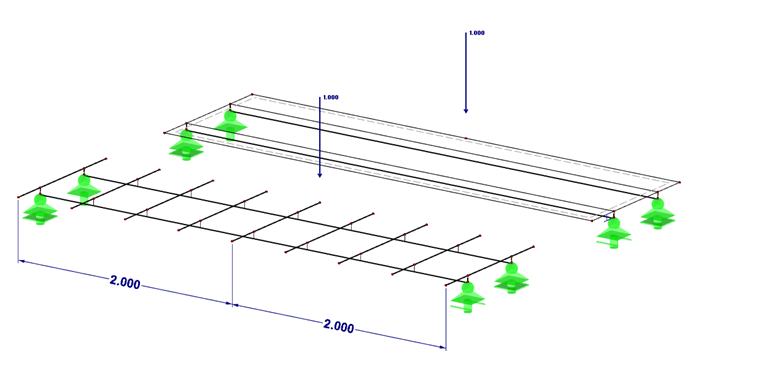
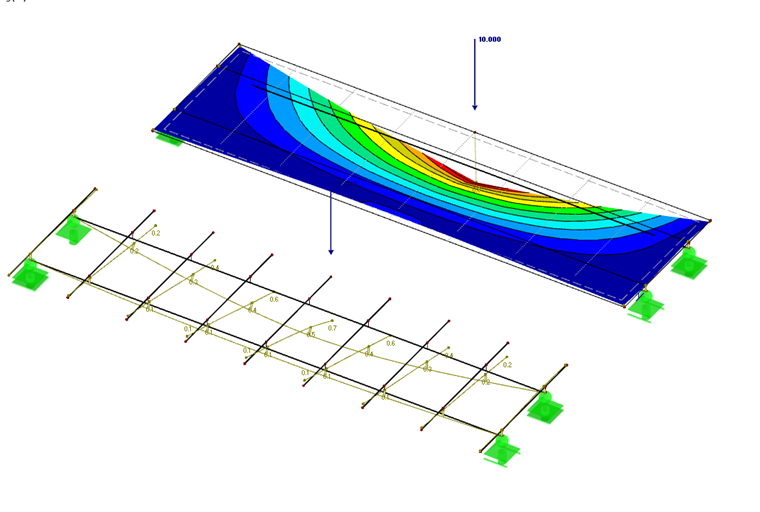
Par exemple, [2] recommande souvent de définir un grillage de poutre. Le grillage représente très bien le comportement structural biaxial de la dalle en béton d'une poutre mixte. Cependant, l'effort de modélisation est plus important dans ce cas, et le grillage est imprécis sur les points discrets locaux. Ci-dessous, la modélisation d'un grillage de poutres est comparée à la modélisation d'une plaque orthotrope.
La définition du grillage à poutres est d'abord décrite à l'aide d'une structure simple. La plaque orthotrope est ensuite définie. Enfin, les résultats et les différences sont expliqués.
Système
- Section acier : HE-A 200
- Matériau acier : S235
- Section béton : d = 100 mm
- Matériau béton : C30/37
- Charges : 5 kN/m²
- Déformation transversale : nu = 0,2
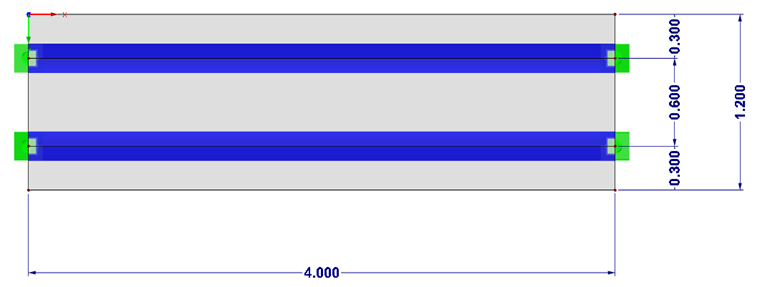
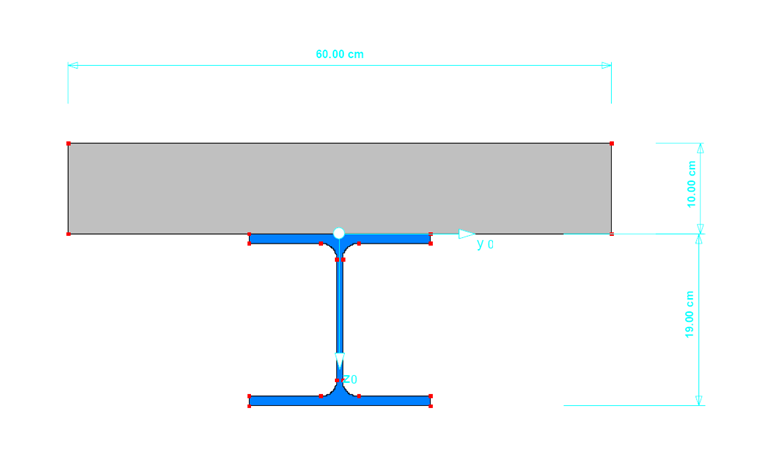
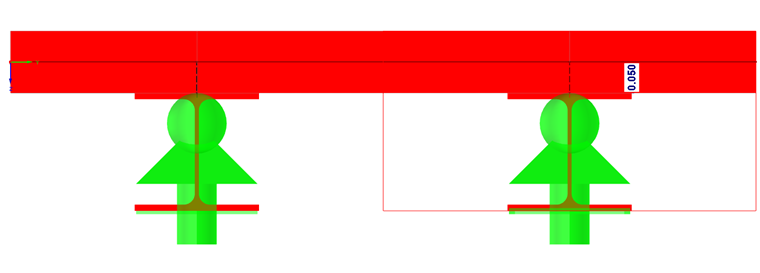
La section mixte est créée dans SHAPE-MASSIVE et importée dans RFEM avec l'excentrement défini par rapport à la dalle en béton. La largeur efficace de la section est supposée être de 60 cm. Le centre de gravité de la section est légèrement décalé de 0,8 cm vers le haut par rapport au joint entre le béton et l'acier. Le joint est donc pris en compte pour les appuis. décalés de 5 cm vers le bas.
Le schéma d'appui lui-même a été sélectionné de manière à ce qu'aucun maintien ne se produise en raison d'une déformation bloquée.
La charge est appliquée de manière identique pour les deux systèmes.
- CC1 = 5 kN/m²
- LC2 = 10 kN (direction x = mi-travée, direction y = bord extérieur)
Structure de grillage de poutre
Exigences du grillage des poutres (d'après [1] ) :
- hauteur de construction constante
- pont à poutres droites
- section symétrique simple
- Les deux poutres principales sont appuyées sur chaque axe d'appui, qui est perpendiculaire à l'axe longitudinal du pont.
- Raidisseurs transversaux presque rigides dans les axes d'appui
- gauchissement non maintenu dans les axes d'appui
- Le logiciel de calcul de structures pour l'analyse des fermes doit pouvoir calculer les éléments de barre.
Valeur calculée de la rigidité en flexion (à partir de [2]) :
Valeur calculée de la rigidité en torsion :
Propriétés de section :
- IT = 0 cm 4
- Iy = (100cmx (10cm)³)/12 = 8 333,3 cm 4
- A = 1 000 cm²
- Ay = 833 cm²
L'entrée est effectuée dans le programme à l'aide des propriétés de section efficace. La rigidité en cisaillement des barres est prise en compte. La rigidité de la dalle en béton est déterminée dans la direction transversale (largeur = 1 m).
Structure en plaques orthotropes
Dans la structure en plaques orthotropes, les poutres principales sont modélisées de la même manière que dans le grillage de poutres. Ces poutres sont ensuite intégrées dans la semelle en béton. La rigidité est entièrement transférée par les poutres principales dans la direction longitudinale et par la semelle en béton dans la direction transversale. Le maillage EF est défini de manière identique à la distance de la poutre secondaire à 50 cm.
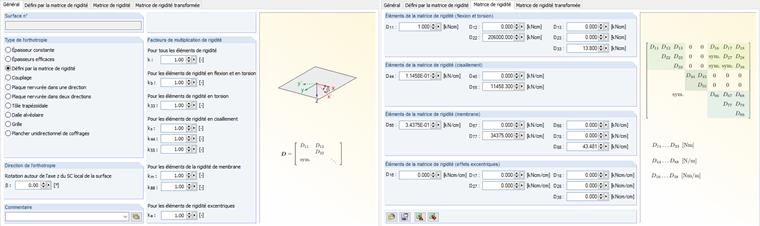
La matrice de rigidité de la plaque orthotrope est symétrique et n'est appliquée qu'aux diagonales principales. Les rigidités pour la flexion dans la direction longitudinale de la plaque et la torsion sont définies de la même manière que les barres transversales du grillage de poutre avec presque zéro.
Valeur calculée de la rigidité en flexion :
Valeur calculée de la rigidité en torsion :
Dans le programme, les données sont entrées à l'aide des rigidités définies par l'utilisateur.
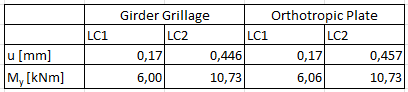
Résumé