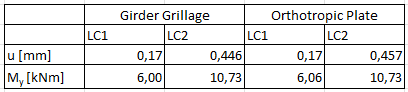
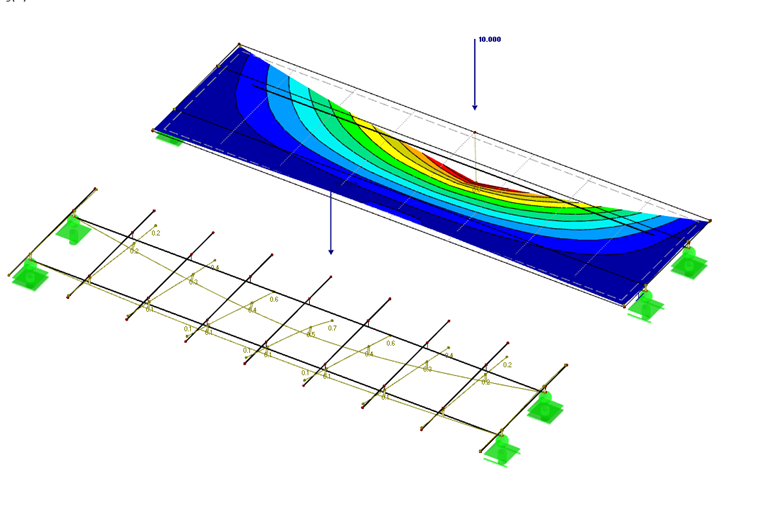
Например, в [2] часто рекомендуется определять балочный ростверк. Ростверк очень хорошо отображает двухосное структурное поведение бетонной плиты из композитной балки. Однако в этом случае требуется больше усилий по моделированию, а ростверк неточен в отдельных точках. Ниже моделирование балочного ростверка сравнивается с моделированием ортотропной плиты.
Сначала описывается определение ростверка с помощью простой конструкции. Затем определяется ортотропная пластина. Наконец, объясняются результаты и различия.
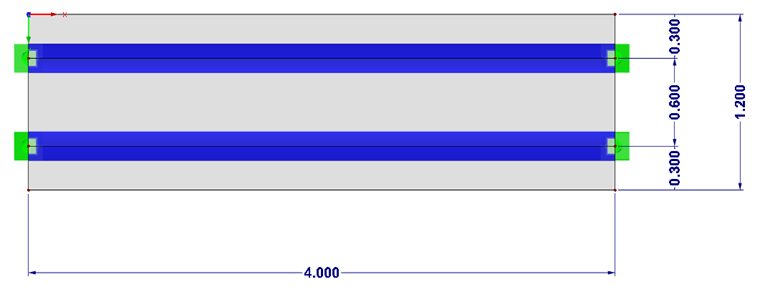
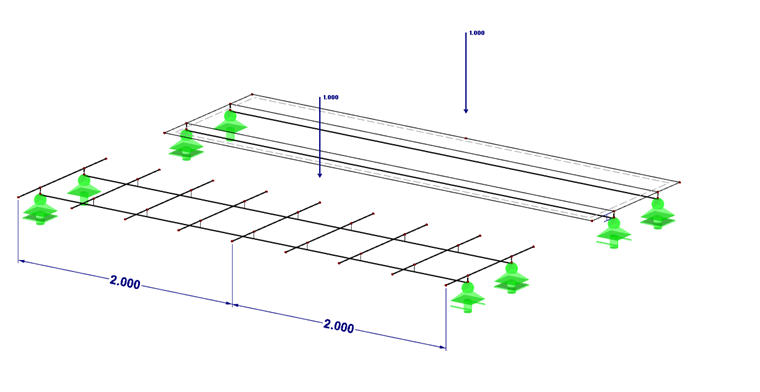
Система
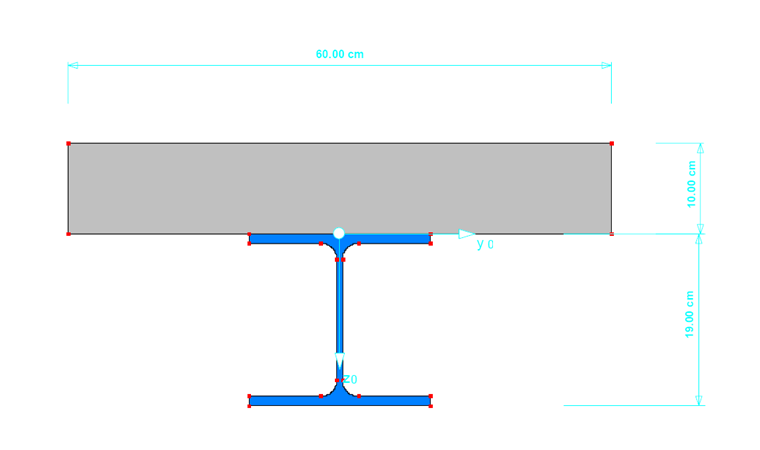
- Сечение стали: HE-A 200
- Материал стали: S235
- Поперечное сечение бетона: d = 100 мм
- Материал бетон: C30/37
- Нагрузки: 5 кН/м²
- Поперечная деформация: nu = 0,2
Составное сечение создается в SHAPE-MASSIVE и импортируется в RFEM с заданным эксцентриситетом сечения по отношению к бетонной плите. Эффективная ширина сечения принята равной 60 см. Центр тяжести сечения немного смещен к стыку между бетоном и сталью на 0,8 см вверх. Поэтому для опор учитывается стык. которые смещены на 5 см вниз.
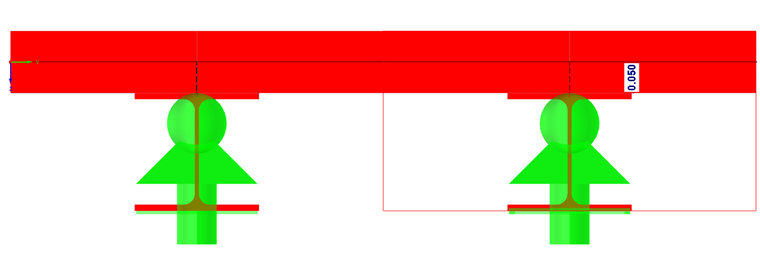
Сама схема опоры подобрана таким образом, чтобы не возникало заеданий из-за сдерживаемой деформации.
Нагрузка одинакова для обеих систем.
- LC1 = 5 кН/м²
- LC2 = 10 кН (направление x = середина пролета, направление y = внешний край)
Балочная конструкция ростверка
Требования к балочным ростверкам (из [1] ):
- постоянная высота конструкции
- мост с прямыми балками
- простое симметричное сечение
- Обе основные балки опираются на каждую опорную ось, которая перпендикулярна продольной оси моста.
- Практически жесткие поперечные ребра жесткости в осях опор
- безудержное коробление в осях опор
- Программное обеспечение для расчета конструкций ферм должно иметь возможность рассчитывать элементы стержней.
Расчетное значение жесткости на изгиб (из [2]):
Расчетное значение жесткости на кручение:
Характ. сечения:
- IT = 0 см 4
- Iy = (100 см x (10 см) ³)/12 = 8 333,3 см 4
- A = 1000 см²
- Ay = 833 см²
Ввод осуществляется в программе с использованием свойств действующего сечения. Учитывается жесткость стержней на сдвиг. Жесткость бетонной плиты определяется в поперечном направлении (ширина = 1 м).
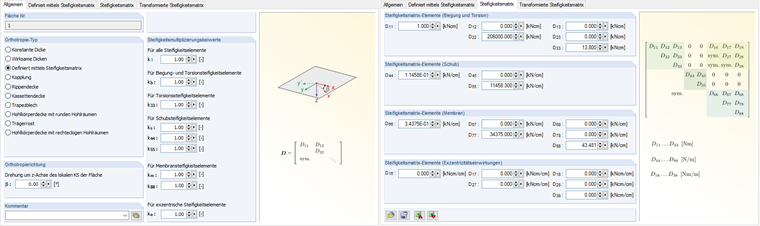
Ортотропная пластина
В конструкции из ортотропных плит основные балки моделируются так же, как и в балочном ростверке. Затем эти балки интегрируются в бетонную полку. Жесткость полностью передается главными балками в продольном направлении и бетонной полкой в поперечном направлении. Размер ячейки КЭ определяется точно так же, как расстояние до вторичной балки - 50 см.
Матрица жесткости ортотропной пластины симметрична и применяется только к главным диагоналям. Жесткости на изгиб в продольном направлении плиты и кручение определяются идентично поперечным стержням балочного ростверка с почти нулевым значением.
Расчетное значение жесткости на изгиб:
Расчетное значение жесткости на кручение:
В программе данные вводятся с использованием значений жесткости, заданных пользователем.
Заключение