In zum Beispiel [2] wird häufig die Definition eines Trägerrosts empfohlen. Mit einem Trägerrost kann das zweiachsige Tragverhalten der Betonplatte eines Verbundträgers ebenfalls gut abgebildet werden. Allerdings ist der Modellierungsaufwand hierzu größer und an lokalen diskreten Punkten ist der Trägerrost ungenauer. Im Folgenden wird die Modellierung eines Trägerrosts mit der einer orthotropen Platte verglichen.
Nach dem System wird die Definition des Trägerrosts anhand eines einfachen Systems beschrieben, anschließend die der orthotropen Platte. Abschließend werden die Ergebnisse und Abweichungen erläutert.
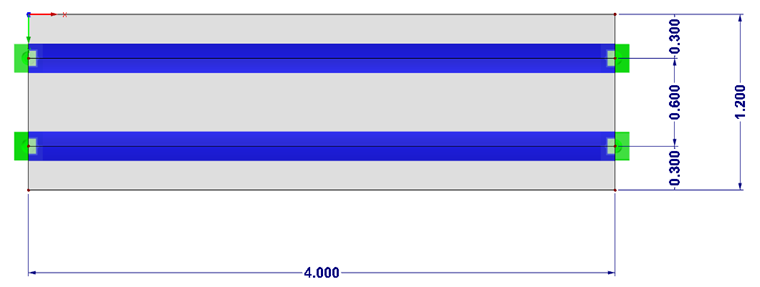
System
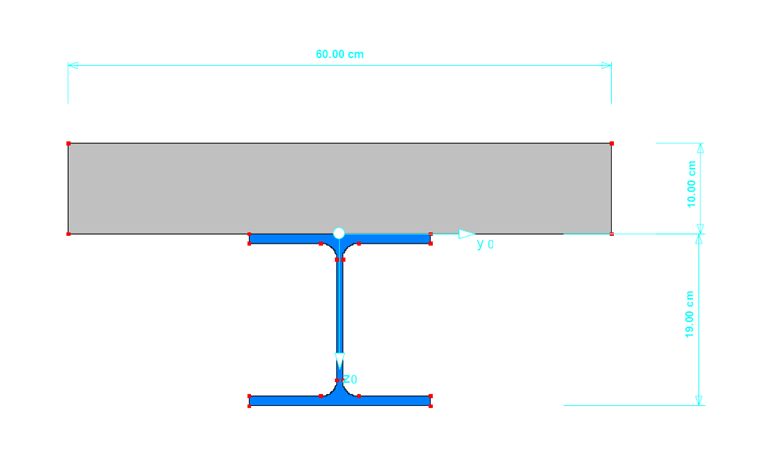
- Querschnitt Stahl: HE-A 200
- Material Stahl: S235
- Querschnitt Beton: d = 100 mm
- Material Beton: C30/37
- Belastung: 5 kN/m²
- Querdehnung: nu=0,2
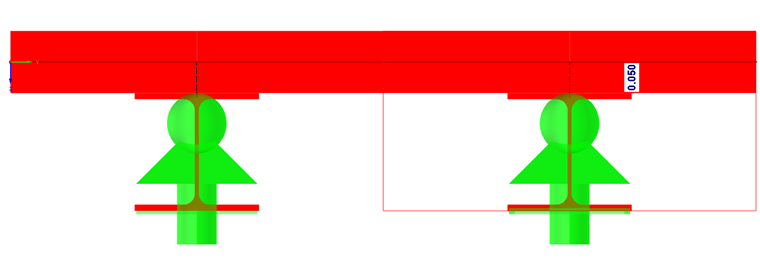
Der Verbundquerschnitt wird in DICKQ erzeugt und mit der definierten Exzentrizität des Querschnitts zur Betonplatte in RFEM eingelesen. Die mitwirkende Breite des Querschnitts wird hierbei pauschal mit 60 cm angesetzt. Der Schwerpunkt des Querschnitts verschiebt sich gegenüber der Fuge zwischen Beton und Stahl um 0,8 cm nach oben. Für die Lagerung wird daher mit der Fuge gerechnet. Die Lager werden dafür um 5 cm nach unten verschoben.
Das Lagerschema selbst wurde so gewählt, dass keine Zwängungen aus behinderter Verformung entstehen.
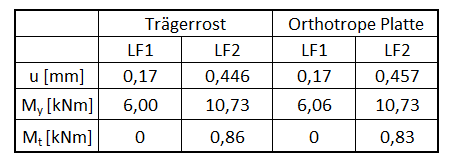
Die Last wird für beide Systeme identisch aufgebracht.
- LF1 = 5 kN/m²
- LF2 = 10 kN (x-Richtung = Feldmitte, y-Richtung = äußerer Rand)
Trägerrostsystem
Voraussetzungen Trägerrost (aus [1]):
- konstante Bauhöhe
- gerade Balkenbrücke
- einfach symmetrischer Querschnitt
- In jeder Lagerachse sind beide Hauptträger gelagert, wobei die Lagerachse senkrecht zur Brückenlängsachse verläuft.
- Annähernd starre Queraussteifungen in den Lagerachsen
- unbehinderte Verwölbung in den Lagerachsen
- Das verwendete Stabwerksprogramm muss schubweiche Stabelemente berechnen können.
Rechenwert der Biegesteifigkeit (aus [2]):
Rechenwert der Torsionssteifigkeit:
Querschnittswerte:
- IT = 0 cm4
- Iy =(100cmx(10cm)³)/12= 8333,3 cm4
- A = 1.000 cm²
- Ay = 833 cm²
Die Eingabe erfolgt im Programm über effektive Querschnittswerte. Schubsteifigkeit der Stäbe wird hierbei berücksichtigt. Steifigkeit wird für die Betonplatte in Querrichtung ermittelt (Breite =1m).
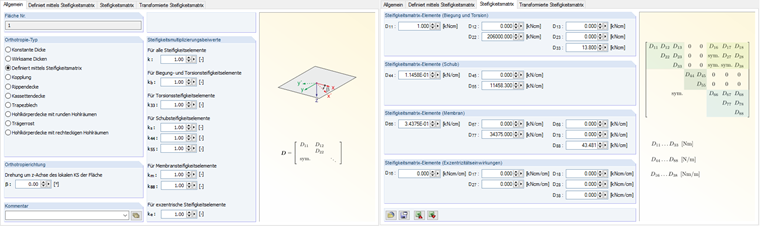
Orthotropes Plattensystem
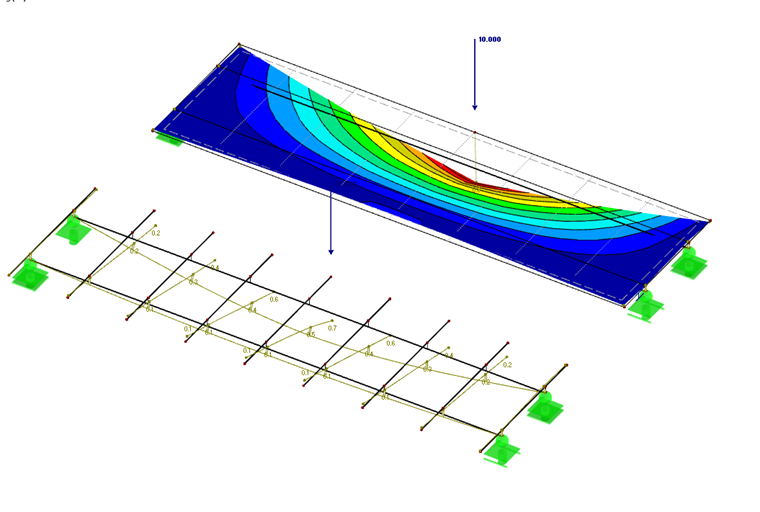
Im orthotropen Plattensystem werden die Hauptträger identisch zum Trägerrost modelliert. Diese Träger werden im Weiteren in die Betonplatte integriert. Die Steifigkeit in Längsrichtung wird komplett von den Hauptträgern übernommen und in der Querrichtung von der Betonplatte. Die FE-Netzgröße wird hierbei identisch zum Abstand der Querträger mit 50 cm definiert.
Die Steifigkeitsmatrix der orthotropen Platte ist symmetrisch und nur auf den Hauptdiagonalen besetzt. Die Steifigkeiten für Biegung in Längsrichtung der Platte und Torsion wurden identisch zu den Querstäben des Trägerrostes mit nahezu null definiert.
Rechenwert der Biegesteifigkeit:
Rechenwert der Torsionssteifigkeit:
Im Programm erfolgt die Eingabe über benutzerdefinierte Steifigkeiten.
Zusammenfassung