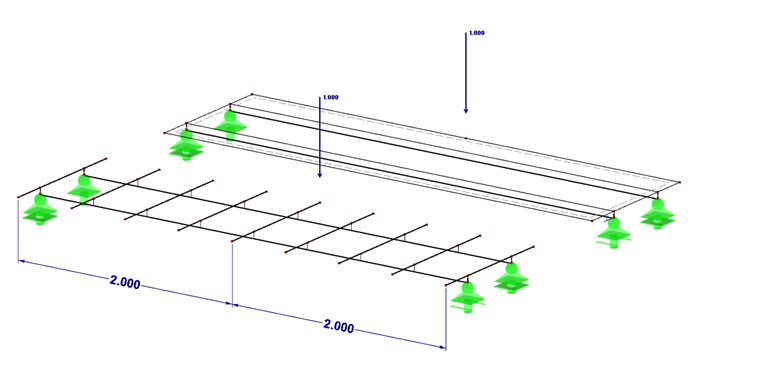
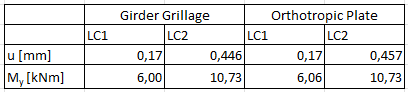
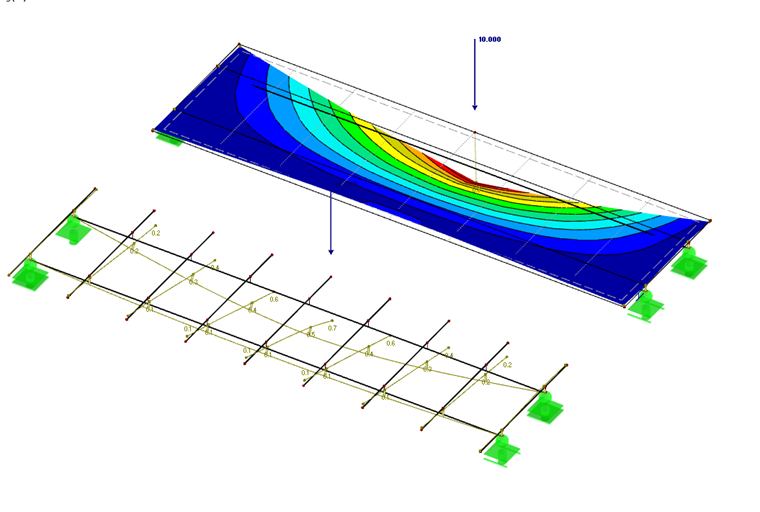
Na przykład [2] często zaleca zdefiniowanie rusztu dźwigarowego. Ruszt bardzo dobrze odzwierciedla zachowanie się dwukierunkowej płyty betonowej belki zespolonej. Jednak w tym przypadku wysiłek związany z modelowaniem jest większy, a kratka jest niedokładna w lokalnych punktach dyskretnych. Poniżej porównano modelowanie rusztu dźwigarowego z modelowaniem płyty ortotropowej.
Najpierw przy użyciu prostej konstrukcji opisano definicję ryflowania dźwigarów. Następnie definiowana jest płyta ortotropowa. Na koniec wyjaśniono wyniki i różnice.
System
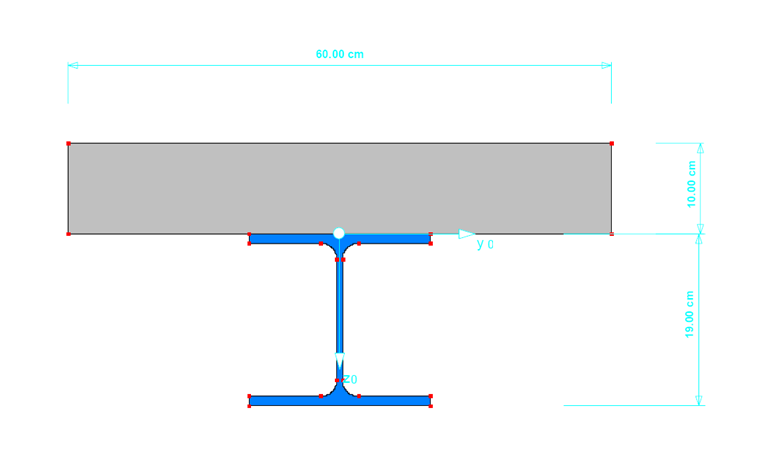
- Przekrój przez stal: HE-A 200
- Materiał stal: S235
- Beton przekroju: d = 100 mm
- Materiał beton: C30/37
- Obciążenie: 5 kN/m²
- Odkształcenie poprzeczne: nu = 0,2
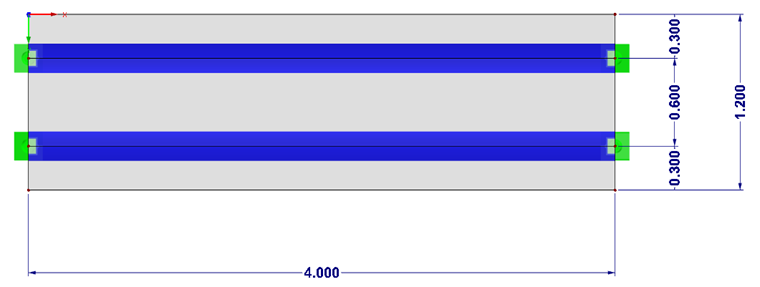
Złożony przekrój jest tworzony w programie SHAPE-MASSIVE i importowany do programu RFEM ze zdefiniowanym mimośrodem przekroju do płyty betonowej. Przyjmuje się, że efektywna szerokość przekroju wynosi 60 cm. Środek ciężkości przekroju jest nieznacznie przesunięty w stosunku do złącza między betonem a stalą o 0,8 cm w górę. Dlatego w przypadku podpór uwzględniane jest połączenie. przesunięte w dół o 5 cm.
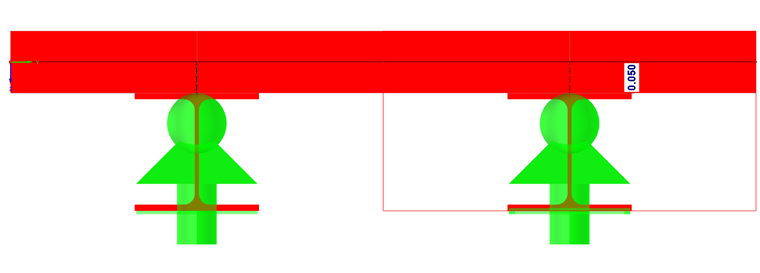
Sam schemat podparcia został wybrany w taki sposób, aby nie występowały utwierdzenia w wyniku stężonego odkształcenia.
Obciążenie jest przykładane identycznie dla obu systemów.
- PO1 = 5 kN/m²
- LC2 = 10 kN (kierunek x = środek rozpiętości, kierunek y = krawędź zewnętrzna)
Konstrukcja kratownicowa
Wymagania dla rusztu dźwigarowego (z [1] ):
- stała wysokość konstrukcyjna
- prosty most dźwigarowy
- prosty przekrój symetryczny
- Obie belki główne podparte są na każdej osi podpory, która jest prostopadła do osi podłużnej mostu.
- Prawie sztywne usztywnienia poprzeczne w osiach podpory
- swobodne skręcenie w osiach podpory
- Oprogramowanie konstrukcyjne do analizy kratownic musi umożliwiać obliczanie elementów prętowych.
Obliczona wartość sztywności na zginanie (z [2]):
Obliczona wartość sztywności na skręcanie:
Ch. przekroju:
- IT = 0 cm 4
- Iy = (100cmx (10cm)³)/12 = 8 333,3 cm 4
- A = 1000 cm²
- Ay = 833 cm²
Wpis jest dokonywany w programie przy użyciu efektywnych właściwości przekroju. Uwzględniana jest sztywność prętów na ścinanie. Sztywność jest określana dla płyty betonowej w kierunku poprzecznym (szerokość = 1 m).
Ortotropowa konstrukcja płytowa
W ortotropowej konstrukcji płytowej główne belki modelowane są w taki sam sposób, jak w przypadku rusztu dźwigarowego. Te dźwigary są następnie zintegrowane z betonowym pasem. Sztywność jest przenoszona w całości przez belki główne w kierunku podłużnym i przez betonowy pas w kierunku poprzecznym. Rozmiar oczka siatki ES jest definiowany identycznie jak odległość belki podrzędnej o długości 50 cm.
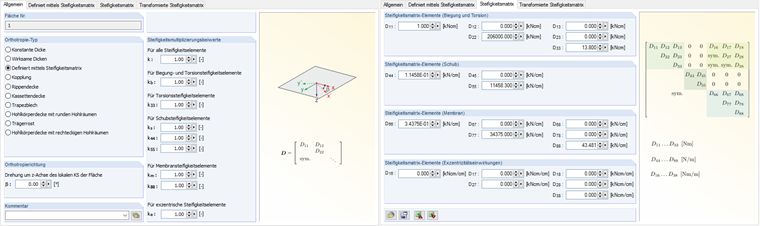
Macierz sztywności płyty ortotropowej jest symetryczna i ma zastosowanie tylko do głównych przekątnych. Sztywności na zginanie w kierunku podłużnym płyty i skręcanie są zdefiniowane identycznie, jak pręty poprzeczne rusztu, z wartością bliską zeru.
Obliczona wartość sztywności na zginanie:
Obliczona wartość sztywności na skręcanie:
W programie dane są wprowadzane przy użyciu sztywności zdefiniowanych przez użytkownika.
Podsumowanie