L'exemple est traité dans [1]. Le calcul selon la section 6.2 de la norme DIN EN 1993-1-8 s'applique aux sections en I et en H et n'est pas applicable dans ce cas. Par conséquent, la méthode CIDECT décrite dans [2] et un modèle aux éléments finis sont utilisés.
Système
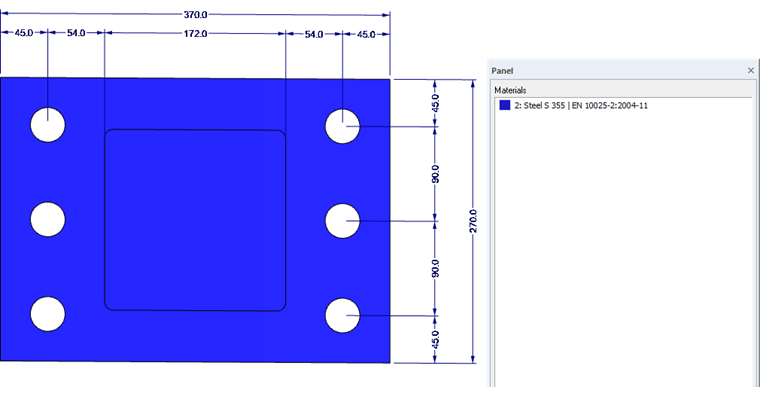
- Section : HE-A 180
- Platine d'about : tp = 35 mm
- Matériau : Acier S355 selon le Tableau 3.1 de la DIN EN 1993-1-1
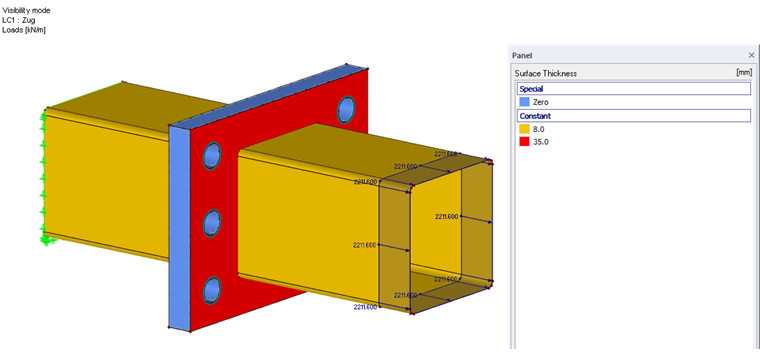
Le modèle aux éléments finis est modélisé à l'aide d'éléments de surface, d'éléments de barre pour les boulons et d'un solide pour représenter le contact des deux platines d'extrémité. Les non-linéarités sont définies pour le solide de contact. Le modèle de matériau sélectionné pour les platines d'about est « Isotrope plastique 2D/3D » (module additionnel RF-MAT NL requis). Ce type de matériau montre un comportement de matériau isotrope dans la zone élastique. Le domaine plastique est basé sur les conditions d'élasticité selon l'hypothèse de distorsion de von Mises avec une limite d'élasticité définie de 35,5 kN/cm².
Efforts internes
La force de calcul déterminante dans la semelle inférieure résultant de la détermination des efforts internes estNEd = 1 491,5 kN (en traction). Si celle-ci est convertie selon le périmètre de la section creuse (ligne centrale), la charge linéique s'élève à 2 211,60 kN/m.
Conception
Le calcul doit inclure la vérification partielle de l'état limite ultime de la platine et le calcul de la charge d'un boulon (y compris la force de contact).
ELU de la platine d'about
La résistance de la platine d'about en flexion est déterminée à l'aide de l'Équation 8.6 de la méthode du CIDECT :
Avec l'Équation 8.5
On obtient le résultat suivant :
Et, par conséquent, le ratio suivant :
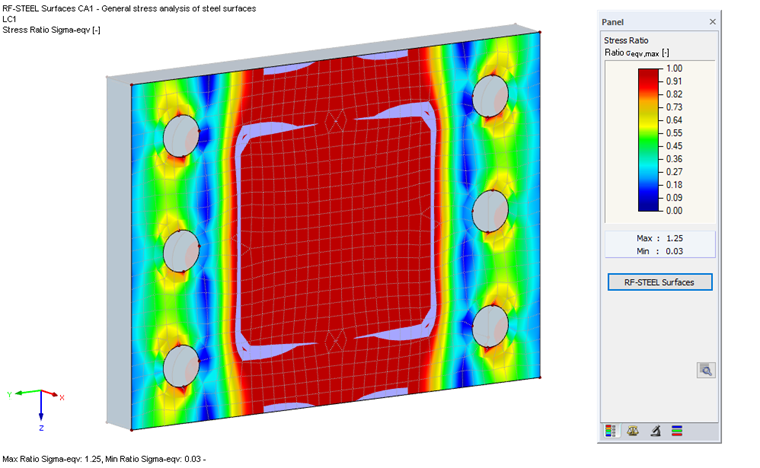
L'évaluation des contraintes dans la platine d'about sur le modèle aux éléments finis avec le module additionnel RF-STEEL Surfaces produit un résultat satisfaisant.
Contraintes sur un boulon
La détermination des contraintes incluant les efforts d'appui est essentielle pour la vérification des boulons. Ces contraintes sont calculées selon l'équation 8.7 avec la méthode CIDECT comme suit :
Avec l'Équation 8.9 :
On obtient le résultat suivant :
Et, par conséquent, le ratio suivant :
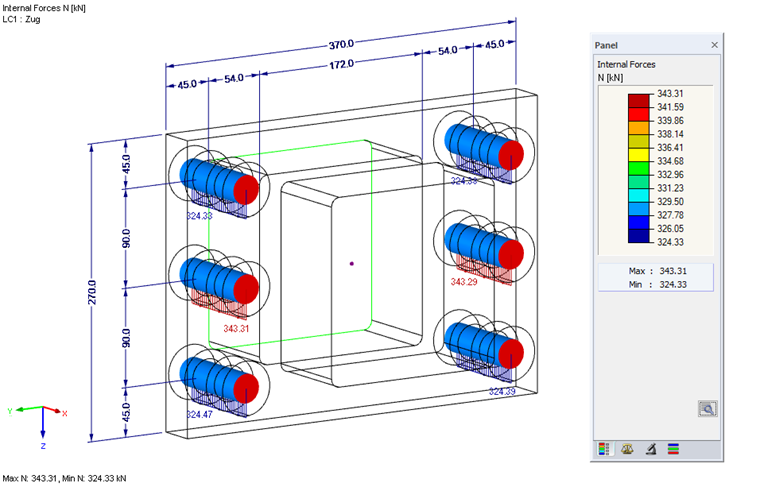
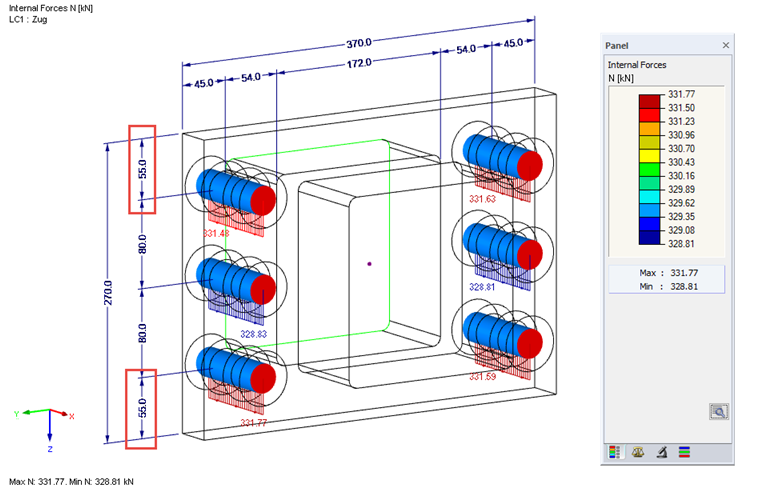
L'évaluation des efforts internes de barre N dans le modèle aux éléments finis produit un effort de calcul par boulon à l'ELU maximal de 343 kN dans les boulons centraux, ce qui est légèrement supérieur au résultat analytique.
Dans [2], la validité du critère de calcul est liée au fait que les axes extérieurs des boulons dans la connexion de la platine d'about ne sont pas situés en dehors des angles de la section creuse. La Figure 8.5 dans [2] ne montre pas l'axe du boulon, mais le trou du boulon comme inclus dans les dimensions de la section creuse.
L'augmentation de la distance au bord à e = 55 mm entraîne une redistribution des efforts de traction dans les boulons extérieurs et une distribution homogène.