Das Beispiel wird in [1] behandelt. Die Bemessung nach Abschnitt 6.2 der DIN EN 1993-1-8 gilt für I- und H-Profile und ist im vorliegenden Fall nicht anwendbar. Es kommen daher das in [2] beschriebene CIDECT-Verfahren sowie ein FEM-Modell zum Einsatz.
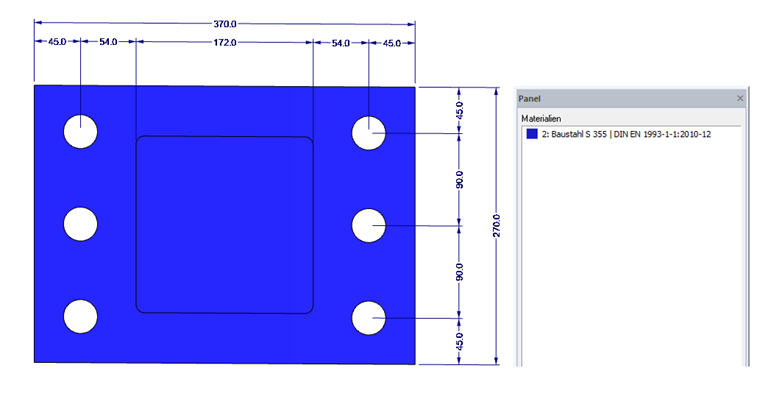
System
Profil: HE-A 180
Stirnplatte: tp = 35 mm
Material: Baustahl S355 nach DIN EN 1993-1-1, Tabelle 3.1
Schrauben: M 30x85 - 10.9/10 - HV
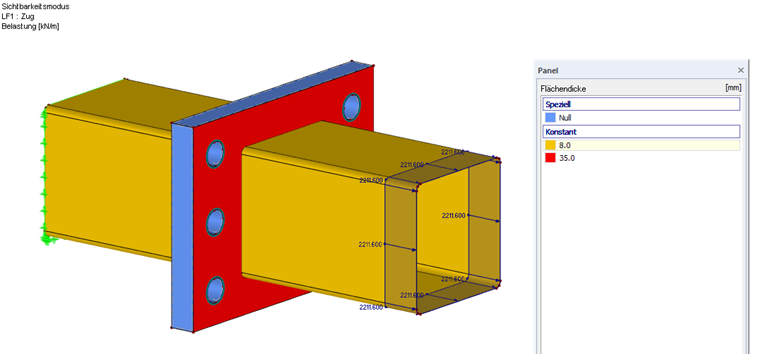
Das FEM-Modell wird modelliert mittels Flächenelementen, Stabelementen für die Schrauben und einem Volumen für die Abbildung des Kontakts der beiden Stirnplatten. Bei dem Kontaktvolumen werden Nichtlinearitäten definiert. Als Materialmodell für die Stirnplatten wird "Isotrop plastisch 2D/3D" gewählt (Voraussetzung dafür ist das Zusatzmodul RF-MAT NL). Bei diesem Materialmodell liegt im elastischen Bereich ein isotropes Materialverhalten vor. Der plastische Bereich basiert auf der Fließbedingung der Verzerrungs-Hypothese nach von Mises mit einer definierten Fließgrenze der Vergleichsspannung von 35,5 kN/cm².
Schnittgrößen
Die sich aus der Schnittgrößenermittlung ergebende maßgebende Bemessungskraft im Untergurt beträgt NEd = 1.491,5 kN (Zug). Wird diese auf den Umfang des Hohlprofiles (Mittellinie) umgerechnet, ergibt sich eine Linienlast von 2.211,60 kN/m.
Bemessung
Die Bemessung soll hier auszugsweise den Nachweis der Tragfähigkeit der Stirnplatte und die Berechnung der Beanspruchung einer Schraube (inklusive Abstützkraft) beinhalten.
Tragfähigkeit der Stirnplatte
Die Ermittlung der Beanspruchbarkeit der Stirnplatte unter Biegebeanspruchung ergibt sich nach Gleichung 8.6 im CIDECT-Verfahren:
Mit Gleichung 8.5
ergibt sich:
Damit erhält man eine Ausnutzung von:
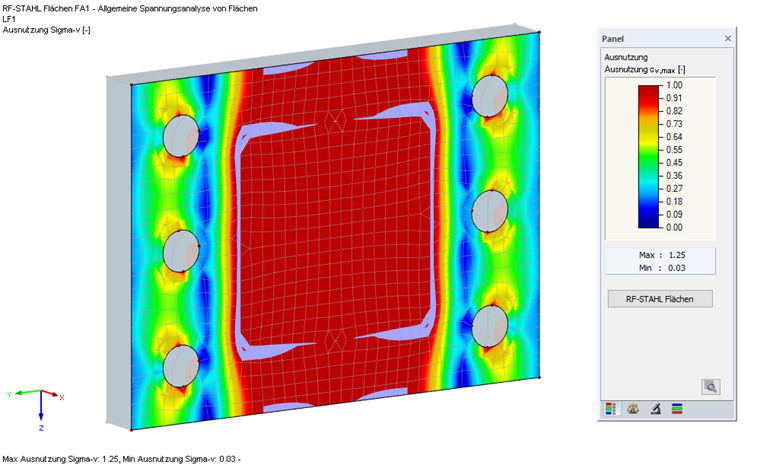
Die Auswertung der Spannungen in der Stirnplatte am FEM-Modell mit dem Zusatzmodul RF-STAHL Flächen ergibt ein adäquates Ergebnis.
Beanspruchung einer Schraube
Für den Nachweis der Schrauben ist die Ermittlung der Beanspruchung inklusive der Abstützkräfte von entscheidender Bedeutung. Diese berechnet sich nach Gleichung 8.7 im CIDECT-Verfahren zu:
Mit Gleichung 8.9
ergibt sich:
Damit erhält man eine Ausnutzung von:
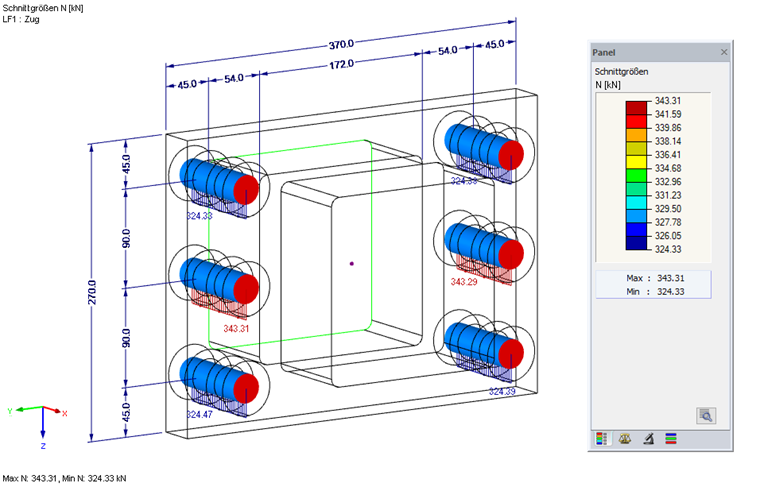
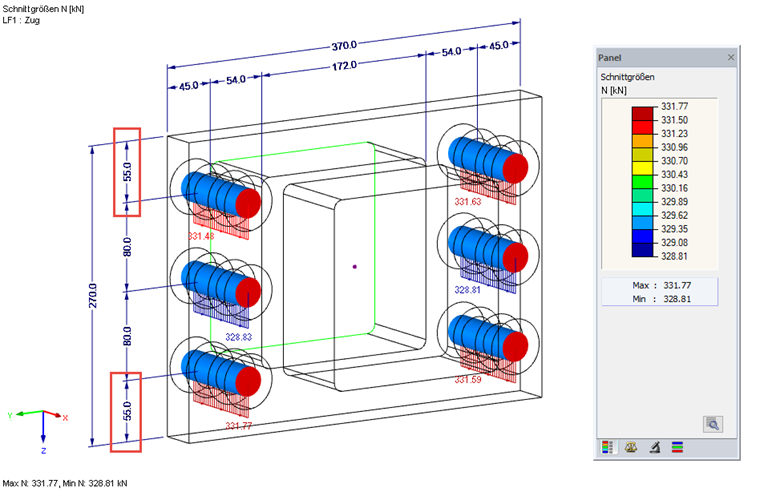
Die Auswertung der Stabschnittgröße N im FEM-Modell ergibt eine maximale Schraubenkraft von 343 kN in den mittleren Schrauben und liegt damit etwas über dem analytischen Ergebnis.
In [2] ist die Gültigkeit des Bemessungskriteriums daran gekoppelt, dass sich die äußeren Schraubenachsen in der Kopfplattenverbindung nicht außerhalb der Ecken des Hohlprofils befinden. Die Abbildung 8.5 in [2] zeigt jedoch nicht die Achse der Schraube, sondern das Schraubenloch als innerhalb der Abmessungen des Hohlprofils liegend.
Eine Erhöhung des Randabstandes auf e = 55 mm ergibt eine Umlagerung der Schraubenkräfte hin zu den äußeren Schrauben und eine im Sinne des Verfahrens homogene Verteilung.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
