Principes théoriques
L'analyse du spectre de réponse consiste à déterminer une réponse modale pour chaque fréquence propre en se basant sur le spectre de réponse défini. Un grand nombre de modes propres peuvent être considérés dans le cas de systèmes complexes. La superposition qui en résulte pose des difficultés car dans la réalité les vibrations propres ne peuvent jamais se produire toutes en même temps à leurs maximums. Pour considérer ce fait dans le calcul, les réponses modales individuelles sont superposées de manière quadratique. L'EN 1998-1 indique deux règles pour effectuer cette opération : la méthode de la combinaison quadratique simple (règle SRSS) et la méthode de combinaison quadratique complète (règle CQC) [1].
L'application de ces règles fournit généralement des résultats réalistes et économiques, contrairement à une simple addition des réponses modales. La superposition ne permet toutefois pas de conserver la direction de l'excitation et donc les signes des résultats. Par conséquent, les résultats sont toujours affichés sous forme de valeurs maximales dans les directions positive et négative. Les efforts internes associés, par exemple, un moment associé à l'effort normal maximal, sont donc perdus. Ce problème peut être contourné en modifiant les règles SRSS et CQC : les formules sont écrites sous forme de combinaison linéaire plutôt que de racines. Cette règle a été créée par le Professeur Dr.-Ing. C. Katz dans l'article [2] et est illustré dans le texte suivant à l'aide de l'exemple de la règle SRSS.
Comparaison des résultats à l'aide d'un exemple
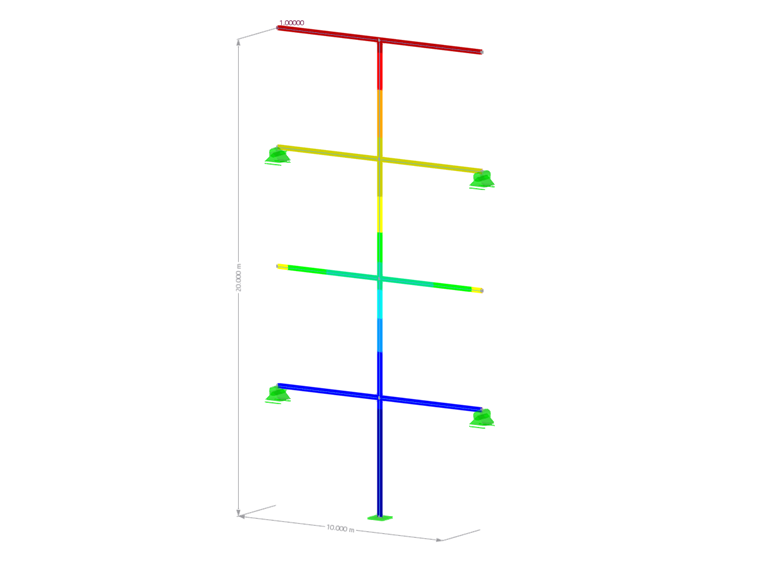
L'effet de la combinaison équivalente linéaire est expliqué à l'aide d'une simple structure acier bidimensionnelle. Trois efforts internes sont considérés : l'effort normal N, l'effort tranchant Vz et le moment My. L'article suivant en est une démonstration à l'aide du module complémentaire Analyse du spectre de réponse dans RFEM 6.
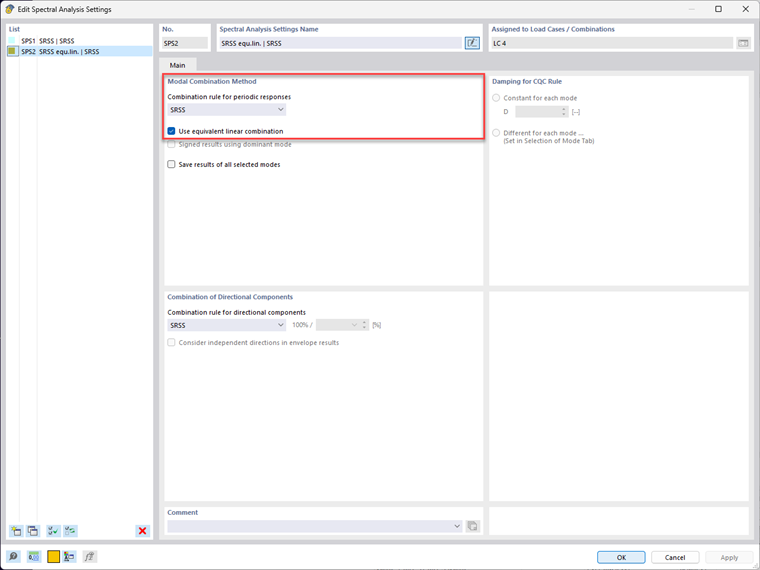
Quatre modes propres sont calculés dans la direction X et un spectre de réponse basé sur l'EN 1998-1 est utilisé. La combinaison linéaire équivalente est activée et l'expression de combinaison sélectionnée dans les « Paramètres pour l'analyse spectrale ».
Les résultats des réponses modales individuelles sont par exemple analysés pour le nœud 5 (sur la barre 6 → côté gauche) et répertoriés dans le tableau suivant :
| Réponse du mode propre 1 | Réponse du mode propre 2 | Réponse du mode propre 3 | Réponse du mode propre 6 | |
|---|---|---|---|---|
| Effort normal N | 1,361 kN | -0,246 kN | 0,815 kN | |
| Effort tranchant VZ | 0,480 kN | -1,635 kN | -0,556 kN | 1,536 kN |
| Moment My | -2,400 kNm | 8,174 kNm | 2,781 kNm |
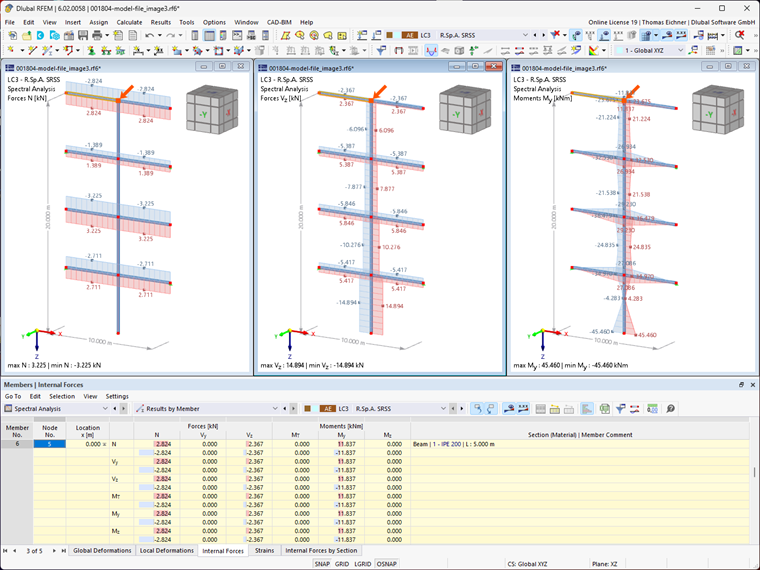
Les valeurs suivantes sont obtenues avec la règle SRSS standard.
Pour évaluer ces résultats dans RFEM, la combinaison de résultats générée est considérée. Les résultats maximaux sont affichés dans le graphique et dans le tableau « Barres - Efforts internes ».
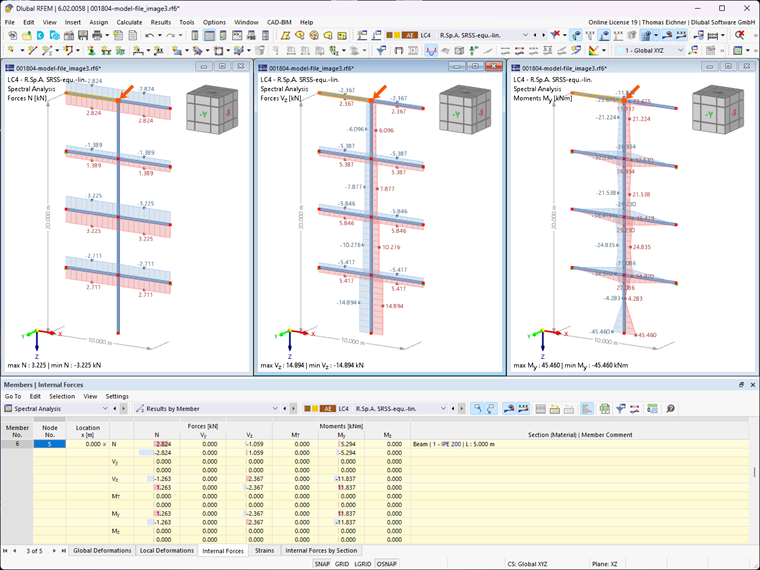
Les efforts internes sont désormais calculés avec la règle SRSS modifiée. En raison de la combinaison équivalente linéaire, les efforts internes sont calculés séparément pour chaque action maximale. Les efforts internes suivants sont obtenus pour l'effort normal maximal :
Cette méthode doit maintenant être appliquée pour toutes les actions. Les efforts internes résultants sont indiqués dans le tableau ci-dessous :
| Effort normal N | Effort tranchant Vz | Moment My | |
|---|---|---|---|
| N max. | 2,823 kN | -1,058 kN | 5,292 kNm |
| N min. | -2,823 kN | 1,058 kN | -5 292 kNm |
| VZ Max | -1 263 kN | 2,367 kN | -11,836 kNm |
| Min VZ | 1,263 kN | -2 367 kN | 11,836 kNm |
| My max. | 1,263 kN | -2 367 kN | 11,836 kNm |
| My min. | -1 263 kN | 2,367 kN | -11,836 kNm |
Seuls les efforts internes maximaux sont affichés graphiquement dans la fenêtre de travail de RFEM tandis que les différences sont bien visibles dans les tableaux.
Conclusion et applications supplémentaires
On peut prouver qu'il est possible de conserver les efforts internes à l'aide d'une combinaison équivalente linéaire. Si cette expression de combinaison est utilisée et importée dans les modules de calcul, les résultats obtenus sont généralement plus économiques. Ceux-ci sont ensuite automatiquement intégrés aux modules complémentaires de calcul.
Il est également possible d'utiliser la combinaison linéaire équivalente en dehors de l'analyse spectrale. Cette option peut être activée pour n'importe quelle combinaison de résultats dans leurs données de base, à condition que la règle SRSS soit utilisée. La méthode est similaire pour la règle CQC. Cependant, la règle CQC peut être utilisée seulement pour les combinaisons de résultats contenant uniquement des cas de charge de la catégorie Séisme et avec les paramètres de la règle CQC définis dans chaque cas de charge.
Il n'est toutefois pas possible de savoir quelle expression de combinaison doit être utilisée pour la vérification. La règle CQC fournit toujours des résultats plus précis car elle peut considérer la pertinence des modes propres rapprochés. La règle SRSS peut être utilisée dans les calculs manuels. Dans les calculs assistés par ordinateur, par exemple dans les analyses dynamiques avec RFEM 6/RSTAB 9, il est recommandé d'utiliser la règle CQC, écrite sous forme de combinaison linéaire, car elle fournit des résultats corrects et économiques dans tous les cas. En outre, le calcul n'est pas sensiblement plus long ni complexe.