Theoretical Background
For each natural frequency, the response spectrum method determines one modal response by means of the defined response spectrum. In the case of complex systems, a large number of mode shapes may need to be considered. The subsequent superposition proves to be difficult because in reality, all natural vibrations would not occur in their full magnitude at the same time. In order to consider this fact in the calculation, the individual modal responses are superimposed quadratically. The European design-relevant standard EN 1998-1 gives two rules for this: the method for the square root of the sum of squares (SRSS rule) and the method of the complete quadratic combination (CQC rule) [1].
Applying these rules usually provides realistic and economical results as opposed to simple addition. However, the direction of the excitation and thus the signs of the results are lost during the superposition. In consequence, the results are always given as maximum values in the positive as well as in the negative direction. Corresponding internal forces and moments (for example, a corresponding moment at the maximum axial force) are lost. This should be avoided by modifying the SRSS and CQC rule: The formulas will be written as a linear combination instead of a root. This rule was introduced by Prof. Dr.-Ing. C. Katz [2] and is shown below using the SRSS rule as an example.
Comparison of Results Using Example
The effect of the equivalent linear combination is explained by a simple two-dimensional steel structure. Three internal forces are considered: axial force N, shear force Vz, and moment My. In the following, it is exemplified using the Response Spectrum Analysis add-on in RFEM 6.
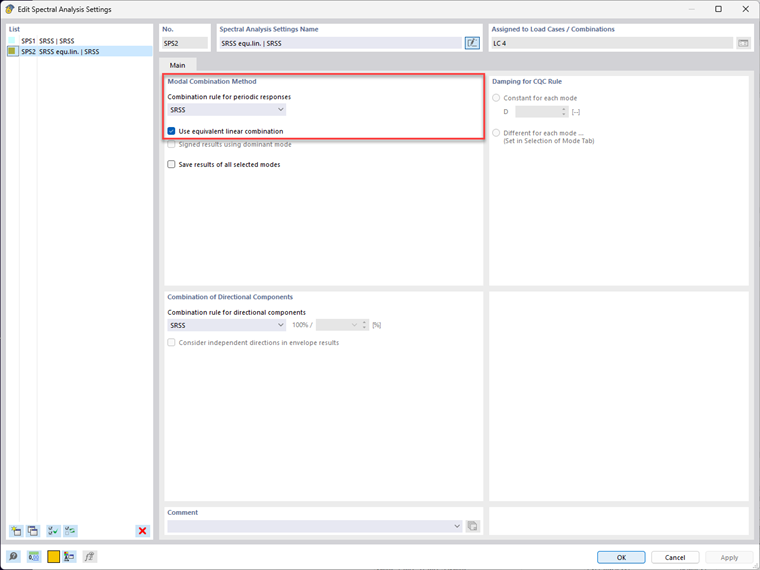
Four mode shapes are calculated in the X-direction and a response spectrum based on EN 1998‑1 is used. Activating the equivalent linear combination and selecting the combination rule is done in the "Spectral Analysis Settings" dialog box.
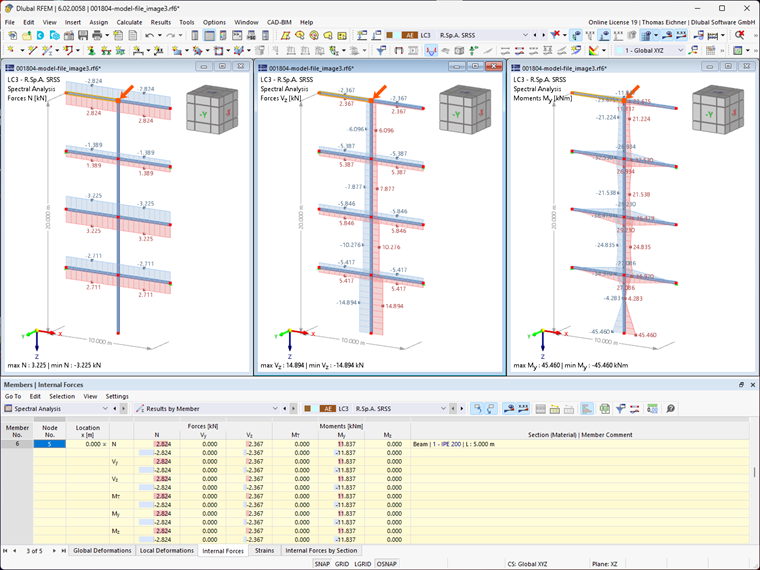
The results of the individual modal responses are analyzed, for example, on Node 5 (on Member 6 → left side) and are listed in the following table.
| Response of Mode Shape 1 | Response of Mode Shape 2 | Response of Mode Shape 3 | Response of Mode Shape 6 | |
|---|---|---|---|---|
| Axial Force N | 1.361 kN | -0.246 kN | 0.815 kN | |
| Shear Force VZ | 0.480 kN | -1.635 kN | -0.556 kN | 1.536 kN |
| Moment My | -2.400 kNm | 8.174 kNm | 2.781 kNm |
The following values result from the standard SRSS rule.
To evaluate these results in RFEM, the generated result combination is considered. The maximum results are shown in the graphic as well as in Table "Members – Internal Forces".
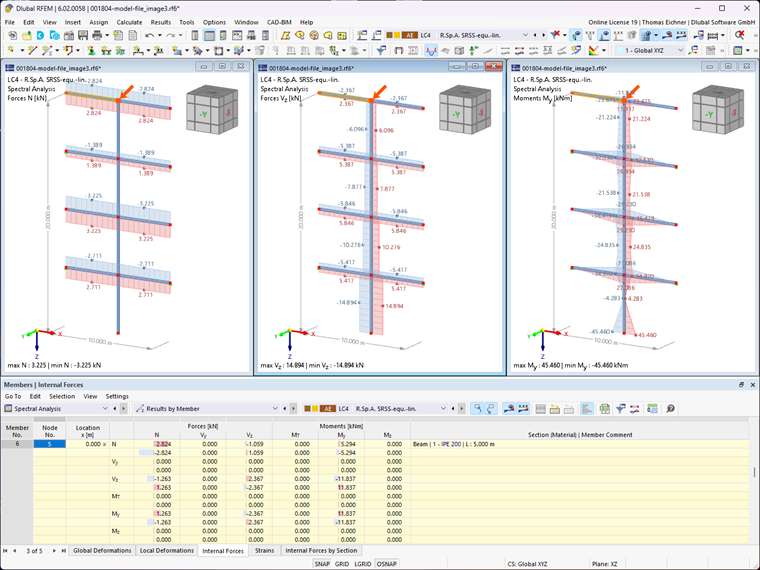
Now the internal forces are calculated by the modified SRSS rule. Due to the equivalent linear combination, the internal forces and moments are calculated separately for each maximum action. The following internal forces result for the maximum axial force.
Now, this procedure must be carried out for all actions. The resulting internal forces and moments are shown in the following table.
| Axial Force N | Shear Force Vz | Moment My | |
|---|---|---|---|
| Max N | 2.823 kN | -1.058 kN | 5.292 kNm |
| Min N | -2.823 kN | 1.058 kN | -5.292 kNm |
| Max VZ | -1.263 kN | 2.367 kN | -11.836 kNm |
| Min VZ | 1.263 kN | -2.367 kN | 11.836 kNm |
| Max My | 1.263 kN | -2.367 kN | 11.836 kNm |
| Min My | -1.263 kN | 2.367 kN | -11.836 kNm |
The graphic in RFEM still shows only the maximum internal forces and moments. However, the differences are visible in the table.
Conclusion and Additional Applications
It was possible to show that the corresponding internal forces are preserved by using the equivalent linear combination. If this combination rule is used and imported into the design modules, you usually get more economical results. These results are then automatically included in the design add-ons.
It is also possible to use the equivalent linear combination outside of the spectral analysis. It can be activated for any result combination in its general data, provided that the SRSS rule is used. The procedure is similar for the CQC rule. However, the CQC rule can only be used for those result combinations in which only load cases of the earthquake category have been used and the parameters of the CQC rule have been defined in the load case itself.
The question that remains unanswered is, which combination rule should finally be used for the design? In any case, the CQC rule provides more accurate results, as it can take into account the relevance of mode shapes lying close to each other. The SRSS rule can be used in manual calculations. In computer-aided calculations, for example for dynamic analyses performed in RFEM 6 / RSTAB 9, we recommend using the CQC rule written as a linear combination, as this provides correct and economical results in all cases. The increased computational effort is negligible.