Podstawy teoretyczne
Metoda spektrum odpowiedzi określa dla każdej częstotliwości drgań własnych jedną odpowiedź modalną na podstawie zdefiniowanego spektrum odpowiedzi. W przypadku złożonych układów konstrukcyjnych może zaistnieć konieczność uwzględnienia dużej liczby postaci drgań własnych. Późniejsza superpozycja odpowiedzi konstrukcji okazuje się być trudna, ponieważ w rzeczywistości nie wszystkie postacie drgań występują w tym samym czasie w pełnym wymiarze. Aby uwzględnić ten fakt w obliczeniach, poszczególne odpowiedzi modalne są superponowane wg. zasady sumacji kwadratów. Europejska norma projektowa EN 1998-1 podaje dwie reguły w tym zakresie: metoda pierwiastka kwadratowego z sumy kwadratów (reguła SRSS) oraz metoda kompletnej kombinacji kwadratowej (reguła CQC) [1].
Zastosowanie tych reguł, w przeciwieństwie do prostego dodawania, daje zazwyczaj realistyczne i bardziej ekonomiczne wyniki. Jednak informacje o kierunku wzbudzenia, a tym samym znakowanie wyników (sił wewnętrznych) zostają utracone podczas takiej superpozycji. W rezultacie wyniki są zawsze podawane jako wartości maksymalne zarówno o znaku dodatnim, jak i ujemnym. Utracone zostają wartości sił odpowiadających, na przykład moment odpowiadający maksymalnej sile osiowej. Należy tego uniknąć i można tego dokonać modyfikując zasadę SRSS i CQC: wzory zostaną zapisane jako kombinacja liniowa zamiast pierwiastka. Diese Regel wurde durch Prof. Dr.-Ing. C. Katz eingeführt [2] und wird nachfolgend am Beispiel der SRSS-Regel gezeigt.
Porównanie wyników na przykładzie obliczeniowym
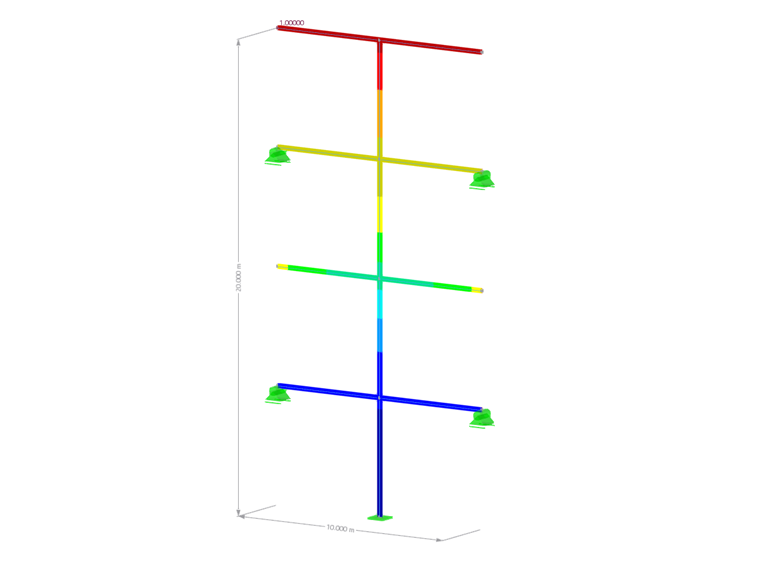
Wpływ równoważnej kombinacji liniowej można zilustrować za pomocą prostej konstrukcji stalowej w 2D. Uwzględniane są trzy siły wewnętrzne: siła osiowa N, siła tnąca Vz i moment My. Im Folgenden wird dies mit Hilfe des Add-Ons Antwortspektrenverfahren in RFEM 6 veranschaulicht.
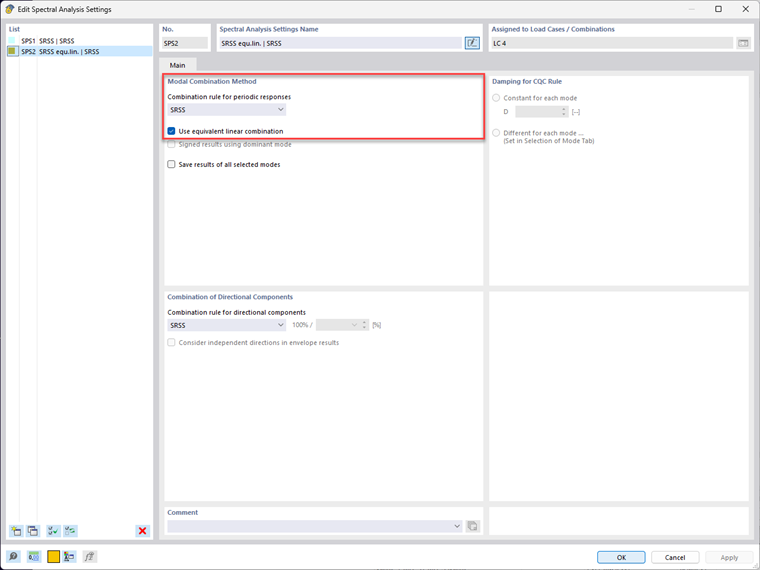
Es werden vier Eigenformen in X-Richtung berechnet und ein Antwortspektrum basierend auf EN 1998-1 verwendet. Die Aktivierung der äquivalenten Linearkombination und die Wahl der Kombinationsregel erfolgt in den "Spektralanalyse-Einstellungen".
Przeanalizujmy wyniki dla poszczególnych odpowiedzi modalnych, na przykład, w węźle nr 5 (na pręcie nr 6 → lewa strona) są one przedstawione w poniższej tabeli.
| Antwort aus Eigenform 1 | Antwort aus Eigenform 2 | Antwort aus Eigenform 3 | Antwort aus Eigenform 6 | |
|---|---|---|---|---|
| Siła osiowa N | 1.361 kN | -0,246 kN | 0.815 kN | |
| Schubkraft VZ | 0.480 kN | -1,635 kN | -0,556 kN | 1,536 kN |
| Moment My | -2.400 kNm | 8.174 kNm | 2.781 kNm |
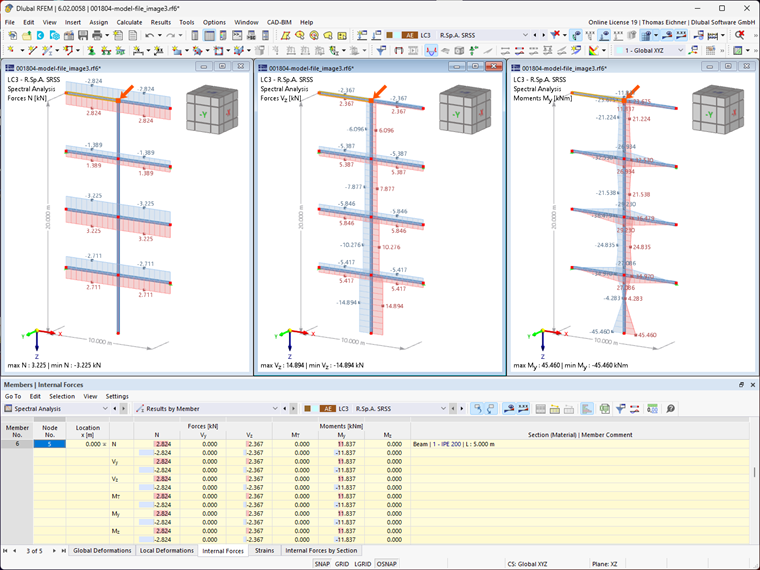
Następujące wartości wynikają ze standardowej reguły SRSS.
Do oceny wyników w programie RFEM brana jest pod uwagę wygenerowana kombinacja wyników. Die maximalen Ergebnisse werden in der Grafik sowie in der Tabelle "Stäbe - Schnittgrößen" dargestellt.
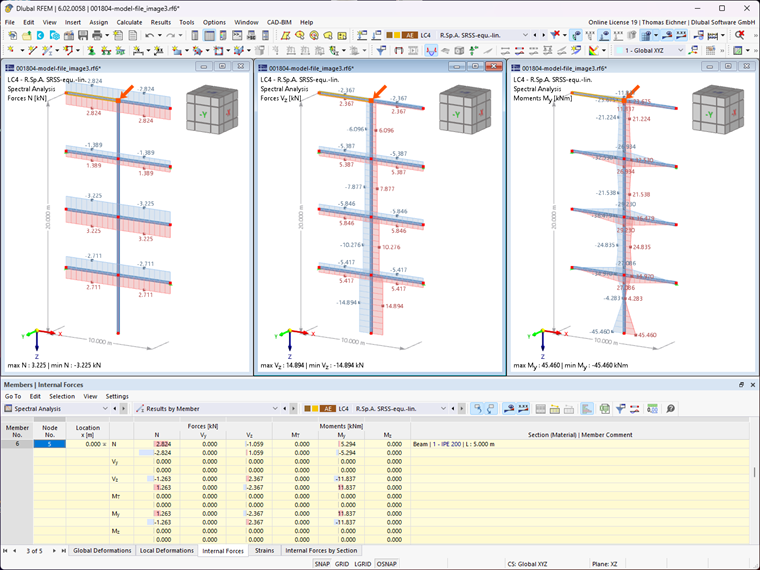
Teraz siły wewnętrzne obliczono według zmodyfikowanej reguły SRSS. Ze względu na równoważną kombinację liniową, siły wewnętrzne i momenty są obliczane osobno dla każdego oddziaływania maksymalnego. Dla maksymalnej siły osiowej wyznaczono następujące siły wewnętrzne.
Teraz tę procedurę należy przeprowadzić dla wszystkich oddziaływań. Wynikowe siły wewnętrzne i momenty przedstawiono w poniższej tabeli.
| Siła osiowa N | Siła tnąca Vz | Moment My | |
|---|---|---|---|
| Max. N | 2.823 kN | -1,058 kN | 5.292 kNm |
| Min. N | -2,823 kN | 1.058 kN | -5,292 kNm |
| Max VZ | -1,263 kN | 2.367 kN | -11,836 kNm |
| Min VZ | 1.263 kN | -2,367 kN | 11.836 kNm |
| Max My | 1.263 kN | -2,367 kN | 11.836 kNm |
| Min My | -1,263 kN | 2.367 kN | -11,836 kNm |
Grafika w programie RFEM nadal pokazuje tylko maksymalne siły wewnętrzne i momenty. Jednak różnice są widoczne w tabeli.
Wnioski i zastosowania
Dzięki zastosowaniu równoważnej kombinacji liniowej można było wskazać odpowiadające siły wewnętrzne. Jeżeli ta reguła kombinacji zostanie zastosowana i zaimportowana do modułów obliczeniowych, zazwyczaj uzyskuje się wyniki korzystniejsze z ekonomicznego punktu widzenia. Diese fließen dann automatisch in die Bemessungs-Add-Ons mit ein.
Es ist ebenfalls möglich, die äquivalente Linearkombination außerhalb der Spektralanalyse zu verwenden. Diese kann für jede beliebige Ergebniskombination in deren Basisangaben aktiviert werden, insofern die SRSS-Regel verwendet wird. Procedura jest podobna w przypadku reguły CQC. Jednak reguła CQC może być stosowana tylko w przypadku tych kombinacji wyników, w których zastosowano tylko przypadki obciążeń z kategorii trzęsienia ziemi, a parametry reguły CQC zostały zdefiniowane w przypadkach obciążenia.
Pozostaje pytanie, która reguła kombinacji powinna być ostatecznie zastosowana do obliczeń. W każdym przypadku reguła CQC zapewnia dokładniejsze wyniki, ponieważ może uwzględniać wpływ postaci drgań o zbliżonej częstotliwości. Reguła SRSS może być stosowana w obliczeniach ręcznych. In computergestützten Berechnungen, beispielsweise in Dynamischen Analysen mit RFEM 6 / RSTAB 9, wird die Verwendung der CQC-Regel, geschrieben als Linearkombination, empfohlen, da dies in allen Fällen korrekte und wirtschaftliche Ergebnisse liefert. a wysiłek włożony w przeprowadzanie obliczeń jest niewielki.