Estacas são representadas como vigas no RFEM. Esta viga está conectada ao solo circundante, podendo assim transmitir forças. A modelagem está descrita no capítulo para os Tipos de barras: Estaca e Ancoragem. A conexão ocorre através de atrito na superfície lateral e pressão na ponta.
Implementação no RFEM
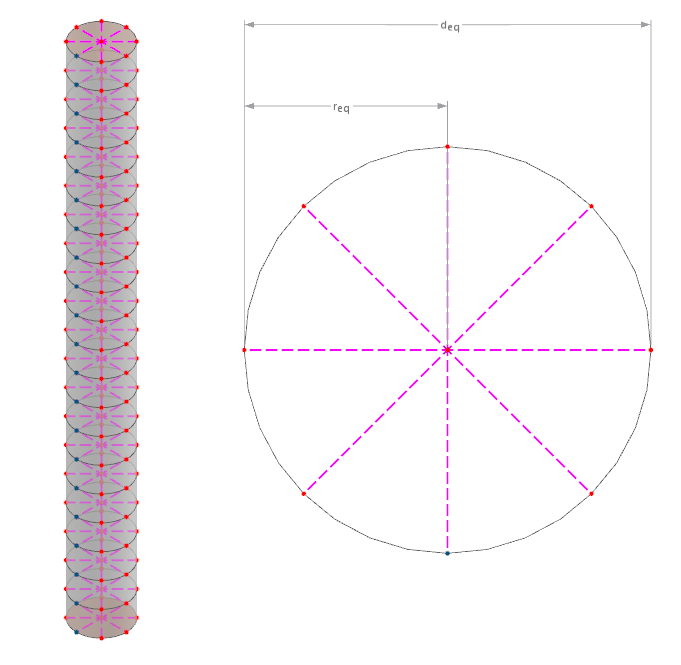
A conexão entre a estaca e o volume de solo circundante é realizada no RFEM atualmente por meio de uma liberação, que pode ser imaginada como uma roda de raios de oito braços. Essas rodas de raios têm seu centro em cada nó EF da barra. A liberação apresenta um comportamento linear-elástico ideal-plástico, definido pelas resistências da estaca. A barra é assumida como um cilindro, possivelmente com seção transversal variável ao longo de seu comprimento. O diâmetro é derivado a partir da área de seção transversal assumida como circular. Os pontos finais dos acoplamentos rígidos são então conectados ao malha volumétrica do solo circundante ponderadamente sobre suas distâncias quando da malhagem independente. A imagem a seguir ilustra isso esquematicamente:
O diâmetro equivalente pode ser calculado, portanto, como mostrado na seguinte fórmula.
Resistências da Estaca
Cálculo das Resistências
O cálculo da resistência ao cisalhamento pode ser realizado pela extensão de ligação e pelo diâmetro equivalente, a partir da resistência total ao cisalhamento. A fórmula abaixo mostra isso assumindo uma resistência ao cisalhamento e seção constante.
|
Fr,s |
Resistência total de fuste de estaca (atrito) |
|
deq |
Diâmetro equivalente de estaca (área circular) |
|
lb |
Comprimento de ligação de estaca |
A determinação da resistência axial na ponta da estaca a partir da resistência total também pode ser realizada pelo diâmetro equivalente da estaca, como mostra a fórmula seguinte.
|
Fr,b |
Resistência total da ponta da estaca |
|
deq |
Diâmetro equivalente de estaca (superfície circular) |
Cálculo de Rigidezes
O cálculo da rigidez pode ser realizado a partir de testes de carga e/ou valores empíricos. Uma outra opção é oferecida por Franz Tschuchnigg através de fórmulas empiricamente determinadas em sua dissertação [1]. A seguir, estas são apresentadas para atrito na superfície lateral e rigidez axial. Adicionalmente, fatores de ajuste recomendados para entrada no RFEM estão incluídos aqui.
|
|
Módulo de corte do solo de enchimento (com coeficiente de Poisson e módulo de elasticidade; Módulo de elasticidade para modelo de material não linear: simples (por exemplo, Mohr-Coulomb), primeira carga Eprim ou de ordem superior (por exemplo, Hardening-Soil) Eur~5 x E(50),prim) |
|
Γs |
Fator de correção do fuste da estaca (empírico; recomendação: 1) |
|
Δs |
Valor inicial do atrito na superfície (empírico; valor recomendado: 0) |
|
fs,RF |
Fator de ajustamento no RFEM (valor recomendado: 0,1) |
|
G |
Módulo de corte de solo intacto (a partir do coeficiente de Poisson e módulo de elasticidade; Módulo de elasticidade para material não linear: simples (por exemplo, Mohr-Coulomb) primeira carga Eprim ou de ordem superior (por exemplo, Hardening-Soil) Eur~5 x E(50),prim) |
|
Γb |
Fator de ajuste para ponta de estaca (empírico; recomendado: 5 a 10) |
|
req |
Raio equivalente da ponta de estaca |
|
fb,RF |
Fator de ajuste do RFEM (valor recomendado: 0,01) |
Substituindo os valores recomendados, pode-se realizar a entrada de atrito na superfície lateral e rigidez axial através das seguintes fórmulas.
|
|
Módulo de corte do solo (a partir do coeficiente de Poisson e do módulo de elasticidade; módulo de elasticidade para modelo de material não linear: simples (por ex.: Mohr-Coulomb) carga inicial Eprim ou de ordem superior (por ex.: Hardening-Soil) Eur~5 x E(50),prim)) |
|
req |
Raio equivalente da ponta da estaca |