Pfähle werden in RFEM als Balken abgebildet. Dieser Balken ist mit dem umliegenden Boden verbunden und kann hierdurch Kräfte einleiten. Die Modellierung ist im Kapitel für die Stabtypen Pfahl und Anker beschrieben.
Die Verbindung erfolgt über Reibung in der Mantelfläche und Spitzendruck.
Implementierung in RFEM
Die Verbindung zwischen dem Pfahl und dem umliegenden Bodenvolumen erfolgt in RFEM aktuell über eine Freigabe, welche man sich wie ein achtarmiges Speichenrad vorstellen kann. Diese Speichenräder haben ihr Zentrum an jedem FE-Knoten des Stabes. Die Freigabe weist ein linear-elastisches ideal-plastisches Verhalten auf, dass durch die Pfahlwiderstande definiert ist.
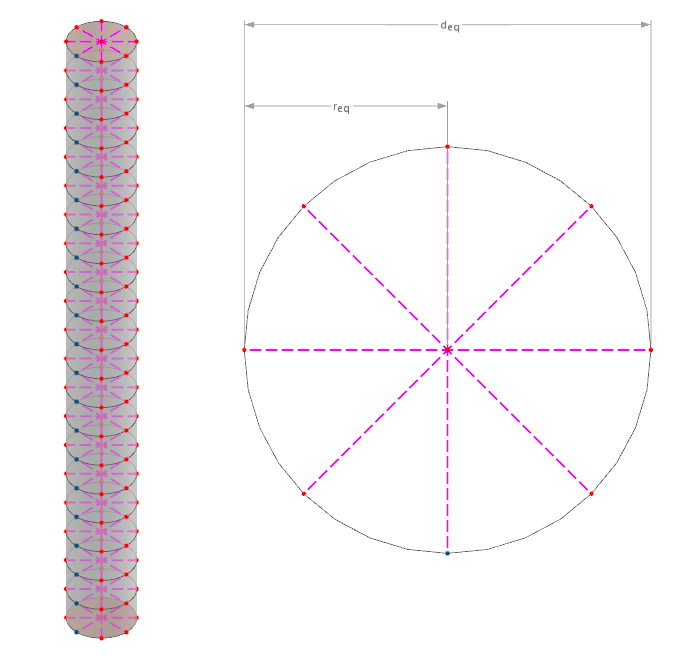
Hierbei wird der Stab als Zylinder angenommen, gegebenenfalls mit veränderlichem Querschnitt entlang dessen Länge. Der Durchmesser ergibt sich aus der als Kreisfläche angenommenen Querschnittsfläche. Die Endpunkte der starren Kopplungen sind daraufhin bei unabhängiger Vernetzung mit dem Volumennetz des umliegenden Bodens gewichtet über deren Abstand verbunden. Nachfolgendes Bild zeigt dies schematisch:
Der äquivalente Durchmesser lässt sich somit wie in folgender Formel gezeigt berechnen.
Pfahlwiderstände
Berechnung Widerstände
Die Berechnung der Schubfestigkeit kann über die Verbundlänge und den äquivalenten Durchmesser aus der Gesamtschubfestigkeit erfolgen. In nachfolgender Formel ist dies für unter Annahme einer konstanten Schubfestigkeit und Querschnitts gezeigt.
|
Fr,s |
Gesamtwiderstand des Pfahlschafts (Reibung) |
|
deq |
Äquivalenter Durchmesser Pfahl (Kreisfläche) |
|
lb |
Verbundlänge Pfahl |
Die Ermittlung der axialen Festigkeit an der Pfahlspitze aus dem Gesamtwiderstand kann ebenfalls über den äquivalenten Pfahldurchmesser erfolgen, wie nachfolgende Formel zeigt.
|
Fr,b |
Gesamtwiderstand der Pfahlspitze |
|
deq |
Äquivalenter Durchmesser Pfahl (Kreisfläche) |
Berechnung Steifigkeiten
Die Berechnung der Steifigkeit kann aus Probebelastungen und/oder Erfahrungswerten erfolgen. Eine weitere Möglichkeit bietet Franz Tschuchnigg durch empirisch bestimmte Formeln in seiner Dissertation [1]. Im Nachfolgenden sind diese für Mantelreibung und axiale Steifigkeit aufgeführt. Zusätzlich sind hier empfohlene Anpassungsfaktoren für die Eingabe in RFEM enthalten.
|
|
Schermodul des anstehenden Bodens (aus Querdehnzahl und Elastizitätsmodul; Elastizitätsmodul für nichtlineare Materialmodell: einfach (z.B. Mohr-Coulomb) Erstbelastung Eprim oder höherer Ordnung (z.B. Hardening-Soil) Eur~5 x E(50),prim) |
|
Γs |
Anpassungsfaktor für Pfahlschaft (empirisch; empfohlen: 1) |
|
Δs |
Anfangswert Mantelreibung (empirisch; empfohlener Wert: 0) |
|
fs,RF |
Anpassungsfaktor RFEM (empfohlener Wert: 0.1) |
|
G |
Schermodul des anstehenden Bodens (aus Querdehnzahl und Elastizitätsmodul; Elastizitätsmodul für nichtlineare Materialmodell: einfach (z.B. Mohr-Coulomb) Erstbelastung Eprim oder höherer Ordnung (z.B. Hardening-Soil) Eur~5 x E(50),prim) |
|
Γb |
Anpassungsfaktor für Pfahlspitze (empirisch; empfohlen: 5 bis 10) |
|
req |
Äquivalenter Radius Pfahlspitze |
|
fb,RF |
Anpassungsfaktor RFEM (empfohlener Wert: 0.01) |
Durch Einsetzen der empfohlenen Werte kann mittels der nachfolgenden Formeln die Eingabe von Mantelreibung und axialer Steifigkeit erfolgen.
|
|
Schermodul des anstehenden Bodens (aus Querdehnzahl und Elastizitätsmodul; Elastizitätsmodul für nichtlineare Materialmodell: einfach (z.B. Mohr-Coulomb) Erstbelastung Eprim oder höherer Ordnung (z.B. Hardening-Soil) Eur~5 x E(50),prim) |
|
req |
Äquivalenter Radius Pfahlspitze |