Los pilotes se representan en RFEM como vigas. Esta viga está conectada al suelo circundante y puede así transmitir fuerzas. La modelización se describe en el capítulo para los Tipos de barra de piloto y anclaje.
La conexión se realiza mediante fricción en la superficie lateral y presión de punta.
Implementación en RFEM
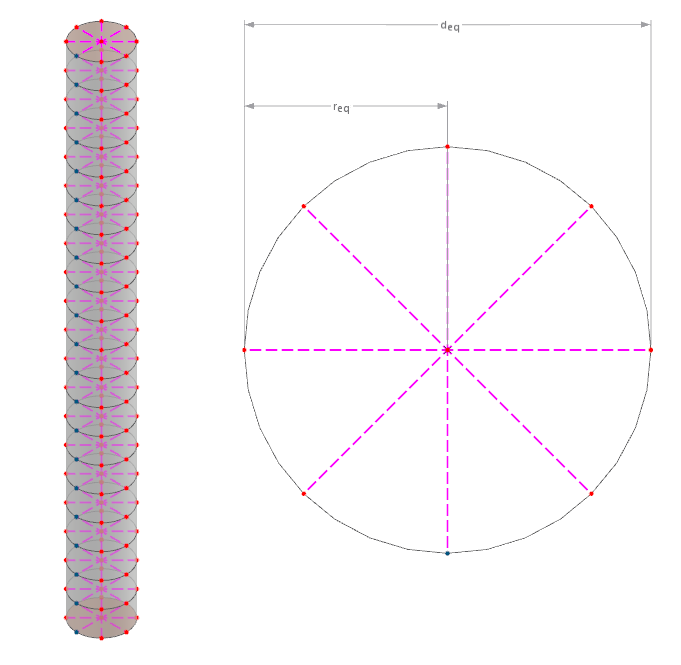
La conexión entre el pilote y el volumen de suelo circundante se realiza en RFEM actualmente a través de una liberación, que se puede imaginar como una rueda de radios de ocho brazos. Estas ruedas de radios tienen su centro en cada nodo EF de la barra. La liberación presenta un comportamiento ideal-plástico lineal-elástico, definido por las resistencias del pilote.
Para ello, se asume que la barra tiene forma cilíndrica, posiblemente con una sección transversal variable a lo largo de su longitud. El diámetro se determina a partir de la superficie de la sección transversal asumida como circular. Los puntos finales de los acoplamientos rígidos se conectan, al estar la malla independientemente con la malla de volumen del suelo circundante, ponderados por su distancia. La siguiente imagen lo muestra esquemáticamente:
El diámetro equivalente se puede calcular de la forma mostrada en la siguiente fórmula.
Resistencias del pilote
Cálculo de resistencias
El cálculo de la resistencia al corte se puede obtener a partir de la longitud de adherencia y el diámetro equivalente a partir de la resistencia total al corte. La siguiente fórmula lo muestra bajo la suposición de una resistencia al corte y una sección constante.
|
Fr,s |
Resistencia total de fuste (fricción) |
|
deq |
Diámetro equivalente de la pila (área circular) |
|
lb |
Longitud de anclaje de la pila |
La determinación de la resistencia axial en la punta del pilote a partir de la resistencia total también se puede realizar a través del diámetro equivalente del pilote, como lo muestra la siguiente fórmula.
|
Fr,b |
Resistencia total de la punta de pilotes |
|
deq |
Diámetro equivalente de pila (área circular) |
Cálculo de rigideces
El cálculo de la rigidez puede hacerse a partir de pruebas de carga y/o valores empíricos. Otra posibilidad es proporcionada por Franz Tschuchnigg a través de fórmulas empíricamente determinadas en su tesis [1]. A continuación, se presentan estas fórmulas para la fricción superficial y la rigidez axial. También se incluyen aquí factores de ajuste recomendados para la entrada en RFEM.
|
|
Módulo de cizalladura de suelo en reposo (a partir del coeficiente de Poisson y el módulo de elasticidad; Módulo de elasticidad para modelo de material no lineal: simple (por ejemplo, Mohr-Coulomb) Carga inicial Eprim o superior (por ejemplo, Hardening-Soil) Eur~5 x E(50),prim) |
|
Γs |
Factor de ajuste para el fuste de pilote (empírico; recomendado: 1) |
|
Δs |
Valor inicial de fricción entre barras (empírico; valor recomendado: 0) |
|
fs,RF |
Factor de ajuste de RFEM (valor recomendado: 0,1) |
|
G |
Módulo de corte del terreno en pendiente (de módulo de cortante y elasticidad; Modulo de elasticidad para material no lineal: Calibración simple (Mohr-Coulomb) Eprim o de orden superior (suelo endurecido) Eur ≈ 5 x E(50),prim) |
|
Γb |
Factor de corrección del extremo de pilote (empírico; recomendado: 5 - 10) |
|
req |
Radio equivalente del tope de pilote |
|
fb,RF |
Factor de ajuste de RFEM (Valor recomendado: 0,01) |
Sustituyendo los valores recomendados, se puede proceder a la introducción de la fricción superficial y la rigidez axial mediante las siguientes fórmulas.
|
|
Módulo de cortante del suelo existente (a partir del coeficiente transversal y el módulo de elasticidad; módulo de elasticidad para modelo de material no lineal: sencillo (por ejemplo, Mohr-Coulomb) primer carga Eprim u orden superior (por ejemplo, suelo endurecido) สุ-5 x E(50),prim) |
|
req |
Radio equivalente de punta de pilote |