Pale są przedstawiane w RFEM jako belki. Ta belka jest połączona z otaczającym gruntem i może w ten sposób przekazywać siły. Modelowanie jest opisane w rozdziale dotyczącym Typy prętów Pale i Kotwy.
Połączenie odbywa się poprzez tarcie na powierzchni zewnętrznej i nacisk końcowy.
Implementacja w RFEM
Połączenie pomiędzy palem a otaczającym go wolumenem gruntu odbywa się w RFEM aktualnie przez zwolnienie, które można sobie wyobrazić jako ośmioramienną szprychę. Te koła szprychowe mają swój środek w każdym węźle MES pręta. Zwolnienie wykazuje liniowo-sprężysto-plastyczne zachowanie, które jest definiowane przez opory pala.
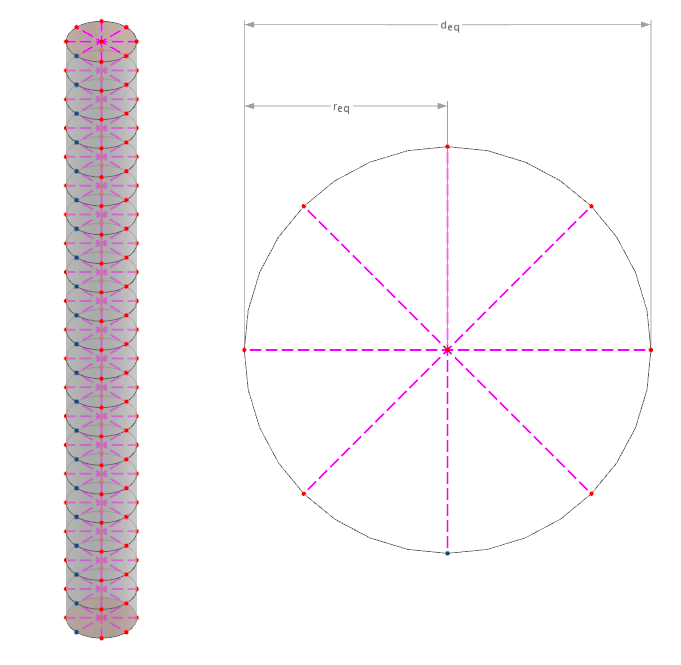
W tym przypadku pręt uważany jest za cylinder, ewentualnie o zmiennym przekroju wzdłuż jego długości. Średnica wynika z powierzchni przekroju poprzecznego, traktowanej jako powierzchnia kołowa. Punkty końcowe sztywnych sprzężeń są następnie przy niezależnym siatkowaniu połączone z siatką volumetyczną otaczającego gruntu w sposób ważony przez ich odległość. Następny obrazek pokazuje to schematycznie:
Równoważną średnicę można zatem obliczyć, jak pokazano w poniższym wzorze.
Opory pala
Obliczanie oporów
Obliczanie wytrzymałości na ścinanie może odbywać się poprzez długość związania i równoważną średnicę z całkowitej wytrzymałości na ścinanie. W poniższym wzorze jest to pokazane przy założeniu stałej wytrzymałości na ścinanie i przekroju.
|
Fr,s |
Całkowita nośność trzonu pala (tarcie) |
|
deq |
Średnica zastępcza pala (powierzchnia koła) |
|
lb |
Długość zespolenia pala |
Określenie wytrzymałości osiowej na końcówce pala z całkowitego oporu można również przeprowadzić poprzez równoważną średnicę pala, jak pokazuje poniższy wzór.
|
Fr,b |
Całkowita nośność końcówki pala |
|
deq |
Średnica zastępcza pala (powierzchnia koła) |
Obliczanie sztywności
Obliczanie sztywności może odbywać się na podstawie próbnych obciążeń i/lub wartości doświadczalnych. Kolejną możliwością jest zastosowanie empirycznie określonych wzorów zaprezentowanych przez Franza Tschuchnigga w jego dysertacji [1]. Poniżej przedstawione są one dla tarcia na powierzchni i osiowej sztywności. Dodatkowo zawarte są tutaj zalecane czynniki dostosowawcze do wprowadzenia w RFEM.
|
|
Moduł ścinania gruntu oporowego (z poprzecznego współczynnika odkształcenia i modułu elastyczności; moduł elastyczności dla nieliniowego modelu materiału: prosty (np. Mohr-Coulomb) początkowe obciążenie Eprim lub wyższego rzędu (np. Hardening-Soil) Eur ~5 x E(50),prim) |
|
Γs |
Współczynnik dostosowawczy dla trzonu pala (empiryczny; zalecany: 1) |
|
Δs |
Wartość początkowa tarcia skorupy (empiryczna; zalecana wartość: 0) |
|
fs,RF |
Współczynnik dopasowania RFEM (zalecana wartość: 0,1) |
|
G |
Skuteczny moduł ścinania gruntu (na podstawie modułu sprężystości i współczynnika Poissona; Moduł sprężystości dla nieliniowego modelu materiału: prosty (np. Mohr-Coulomb) początkowe obciążenie Eprim lub wyższego rzędu (np. materiał ulegający utwardzeniu) Eur~5 x E(50),prim) |
|
Γb |
Współczynnik dostosowania dla ostrza pala (empiryczny; zalecane: 5 do 10) |
|
req |
Promień równoważny ostrza pala |
|
fb,RF |
Współczynnik adaptacji dla RFEM (zalecana wartość: 0,01) |
Przez zastosowanie zalecanych wartości w poniższych wzorach możliwe jest wprowadzenie tarcia na powierzchni i osiowej sztywności.
|
|
Sztywność na ścinanie gruntu (oparta na współczynniku Poissona i module sprężystości; moduł sprężystości dla nieliniowego modelu materiału: prosty (np. Mohr-Coulomb) - Eprim lub wyższego rzędu (np. Hardening-Soil) Eur~5 x E(50),prim) |
|
req |
Promień równoważny ostrza pala |