Dans RFEM, les pieux sont représentés comme des poutres, connectées au sol environnant, permettant ainsi de transférer les forces. La modélisation est décrite dans le chapitre sur les Types de barre Pieu et Ancrage.
La connexion se fait par frottement sur la surface latérale et par pression à la pointe.
Implémentation dans RFEM
La connexion entre le pieu et le solide de sol environnant se fait actuellement dans RFEM par une libération, qu’on peut imaginer comme une roue à rayons à huit bras. Ces roues à rayons ont leur centre à chaque nœud EF de la barre. La libération présente un comportement linéaire-élastique idéalement plastique défini par les résistances du pieu.
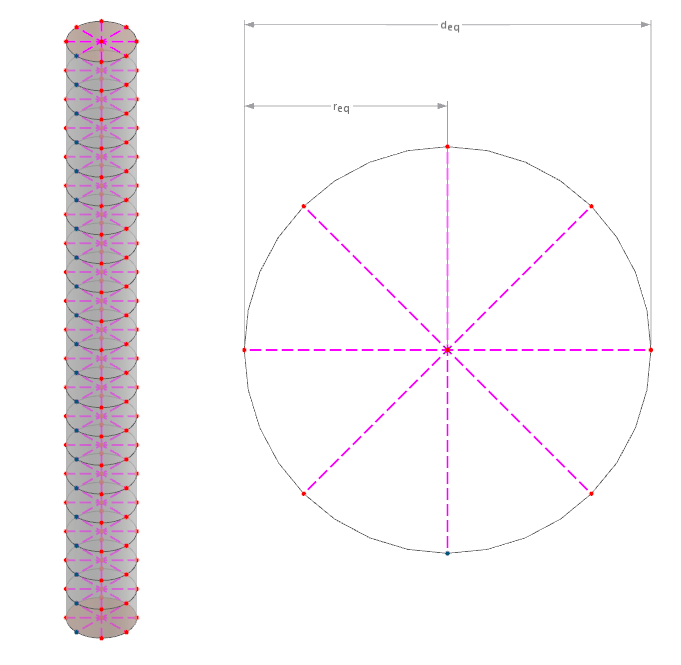
La barre est considérée comme un cylindre, éventuellement de section variable le long de sa longueur. Le diamètre résulte de l’aire de section transversale présumée circulaire. Les points finaux des liaisons rigides sont ensuite connectés, avec une répartition pondérée de leur distance, à la maille volumétrique du sol environnant pour un maillage indépendant. L’image suivante illustre cela de manière schématique :
Le diamètre équivalent peut ainsi être calculé comme le montre la formule suivante.
Résistances du pieu
Calcul des résistances
Le calcul de la résistance au cisaillement peut être effectué via la longueur de liaison et le diamètre équivalent à partir de la résistance totale au cisaillement. La formule suivante illustre cette méthode avec l’hypothèse d’une résistance au cisaillement et d’une section constantes.
|
Fr,s |
Résistance totale du fût du pieu (friction) |
|
deq |
Diamètre équivalent du pieu (surface circulaire) |
|
lb |
Longueur d’ancrage du pieu |
La détermination de la résistance axiale à la pointe du pieu à partir de la résistance globale peut également être effectuée via le diamètre équivalent du pieu, comme le montre la formule suivante.
|
Fr,b |
Résistance totale de la pointe du pieu |
|
deq |
Diamètre équivalent du pieu (surface circulaire) |
Calcul des rigidités
Le calcul de la rigidité peut être réalisé à partir d’essais de charge et/ou de valeurs empiriques. Franz Tschuchnigg propose également des formules empiriques déterminées dans sa thèse [1]. Elles sont présentées ci-après pour le frottement de surface et la rigidité axiale. Des facteurs d’ajustement recommandés pour leur saisie dans RFEM sont également inclus ici.
|
|
Module de cisaillement du sol (extrapolé du module de déformation; module de déformation pour un modèle de matériau non linéaire : simple (par ex. Mohr-Coulomb) chargement primaire Eprim ou d’ordre supérieur (par ex. Hardening-Soil) Eur~5 x E(50),prim) |
|
Γs |
Facteur d’ajustement pour le fut du pieu (empirique ; recommandé : 1) |
|
Δs |
Valeur Initiale frottement Global (empirique ; Valeur recommandée : 0) |
|
fs,RF |
Facteur d’ajustement RFEM (valeur recommandée : 0,1) |
|
G |
Module de cisaillement du sol en place (à partir du coefficient de Poisson de cisaillement et du module d’élasticité ; module d’élasticité pour modèle de matériau non linéaire : simple (par exemple Mohr-Coulomb) Eprim de chargement initial ou d’ordre supérieur (par exemple Hardening-Soil) Eur~5 x E(50),prim) |
|
Γb |
Facteur d’ajustement du sommet du pieu (empirique ; recommandé : 5 à 10) |
|
req |
Rayon équivalent du sommet du pieu |
|
fb,RF |
Facteur d’ajustement RFEM (valeur recommandée : 0,01) |
En insérant les valeurs recommandées, l’entrée du frottement de surface et de la rigidité axiale peut être réalisée à l’aide des formules suivantes.
|
|
Module de cisaillement du sol (à partir du ratio de contrainte de cisaillement et du module d'élasticité ; module d'élasticité pour le modèle de matériau non linéaire : simple (par exemple, Mohr-Coulomb) premier chargement Eprim ou d'ordre supérieur (par exemple, Soil Hardening ) Eure~5 x E(50),prim) |
|
req |
Rayon équivalent à la pointe du pieu |