I pali sono rappresentati in RFEM come travi. Questa trave è collegata al terreno circostante e può quindi trasmettere forze. La modellazione è descritta nel capitolo per i Tipi di asta Palo e Ancoraggio.
Il collegamento avviene tramite attrito sulla superficie laterale e pressione di punta.
Implementazione in RFEM
Il collegamento tra il palo e il volume di terra circostante avviene attualmente in RFEM tramite uno sblocco, che si può immaginare come una ruota a raggi a otto braccia. Queste ruote a raggi hanno il loro centro in ogni nodo FE del'asta. Lo sblocco presenta un comportamento lineare-elastico ideale-plastico definito dalla resistenza dei pali.
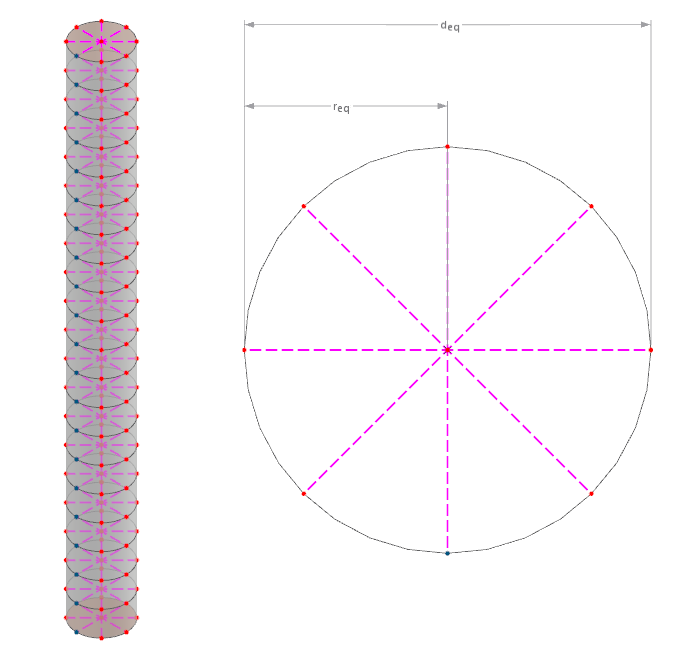
In questo caso, l'asta è assunta come un cilindro, eventualmente con sezione trasversale variabile lungo la sua lunghezza. Il diametro risulta dall'area della sezione trasversale assunta come un cerchio. I punti finali dei collegamenti rigidi sono quindi ponderati in base alla distanza ad essi relativi con la rete volumetrica del terreno circostante se la rete è indipendente. L'immagine seguente lo mostra schematicamente:
Il diametro equivalente può quindi essere calcolato come mostrato nella formula seguente.
Resistenza dei pali
Calcolo delle resistenze
Il calcolo della resistenza al taglio può essere calcolato dalla lunghezza di adesione e dal diametro equivalente partendo dalla resistenza totale al taglio. Nella formula seguente ciò è mostrato assumendo una resistenza costante al taglio e sezione trasversale.
|
Fr,s |
Attrito totale del fusto del palo |
|
deq |
Diametro equivalente della pila (area del cerchio) |
|
lb |
Lunghezza composita del palo |
La determinazione della resistenza assiale alla punta del palo dalla resistenza complessiva può anche avvenire attraverso il diametro equivalente del palo, come mostrato nella formula seguente.
|
Fr,b |
Resistenza totale della sommità del palo |
|
deq |
Diametro equivalente della pila (area circolare) |
Calcolo delle rigidezze
Il calcolo della rigidità può avvenire da prove di carico e/o valori empirici. Un'altra possibilità è offerta da Franz Tschuchnigg attraverso formule empiricamente determinate nella sua dissertazione [1]. Di seguito sono riportate per attrito superficiale e rigidità assiale. Inoltre, sono inclusi i fattori di adattamento consigliati per l'inserimento in RFEM.
|
G |
Modulo di taglio del terreno (dal rapporto di Poisson e modulo elastico; modulo elastico per modello materiale non lineare: semplice (ad esempio Mohr-Coulomb) carico primario Eprim o di ordine superiore (ad esempio Hardening-Soil) Eur~5 x E(50),prim) |
|
Γs |
Fattore di adeguamento per l'estensione del palo (empirico; consigliato: 1) |
|
Δs |
Valore iniziale dell'attrito tra guaina e terreno (empirico; valore raccomandato: 0) |
|
fs,RF |
Fattore di adattamento per RFEM (valore raccomandato: 0.1) |
|
G |
Modulo di taglio del terreno in situ (da modulo di Poisson e modulo elastico; modulo elastico per modello di materiale non lineare: caricamento iniziale semplice (ad es. Mohr-Coulomb) Eprim o di ordine superiore (ad es. Hardening-Soil) Eu,r~5 x E(50),prim)) |
|
Γb |
Fattore di regolazione per la punta del palo (empirico; consigliato: 5-10) |
|
req |
Raggio equivalente della punta del palo |
|
fb,RF |
Fattore di regolazione RFEM (valore raccomandato: 0,01) |
Sostituendo i valori raccomandati, l'inserimento di attrito superficiale e rigidità assiale può essere eseguito tramite le formule seguenti.
|
|
Modulo di taglio del terreno 凊 (derivato dal rapporto di Poisson e il modulo elastico; il modulo elastico per modelli di materiali non lineari: semplice (ad esempio, Mohr-Coulomb) al primo caricamento Eprim o di ordine superiore (ad esempio, suoli induriti) Eur~5 x E(50),prim) |
|
req |
Raggio equivalente della punta del palo |