Пальи отображаются в RFEM как балки. Эта балка соединена с окружающим грунтом и может передавать силы через это соединение. Моделирование описано в главе для Типы стержней Паля и Якорь. Соединение осуществляется через трение на боковой поверхности и контактное давление на конце.
Реализация в RFEM
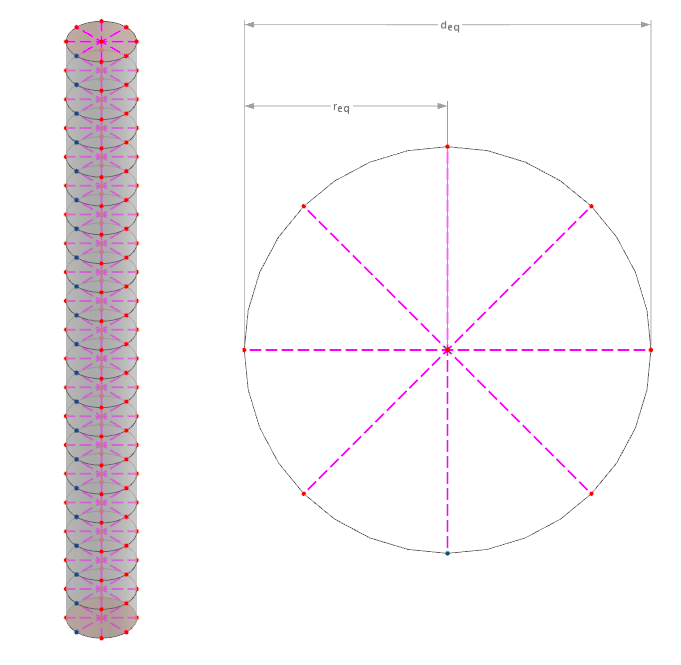
В настоящий момент в RFEM соединение между палью и окружающим ее объемом грунта осуществляется через освобождение, которое можно представить как колесо со спицами, имеющее восемь спиц. Эти спицевые колеса имеют центр в каждом узле конечноэлементной сетки стержня. Освобождение проявляет линейно-упругое идеал-пластическое поведение, которое определяется сопротивлениями пали. При этом стержень принимается как цилиндр, потенциально имеющий изменяющееся поперечное сечение вдоль его длины. Диаметр определяется из площади сечения, принятой как круговая площадь. Затем конечные точки жестких соединений соединяются с сеткой объема окружающего грунта взвешенно по их расстоянию в случае независимой сетки. Следующее изображение схематически показывает это:
Эквивалентный диаметр может быть рассчитан, как показано в следующей формуле.
Сопротивления Пали
Расчет Сопротивлений
Расчет сдвиговой прочности может быть выполнен по длине соединения и эквивалентному диаметру из общей сдвиговой прочности. В следующей формуле это показано для случая постоянной сдвиговой прочности и поперечного сечения.
|
Fr,s |
Полное сопротивление ствола сваи (рение) |
|
deq |
Эквивалентный диаметр сваи (круглая площадь) |
|
lb |
Длина сцепления сваи |
Определение осевой прочности в наконечнике пали из общего сопротивления также может быть выполнено через эквивалентный диаметр пали, как показывает следующая формула.
|
Fr,b |
Общая несущая способность конуса сваи |
|
deq |
Эквивалентный диаметр сваи (круглая поверхность) |
Расчет Жесткостей
Расчет жесткости может быть выполнен на основе пробных нагрузок и/или эмпирических данных. Еще одну возможность предоставляет Франц Чукнигг через эмпирически определенные формулы в своей диссертации [1]. Далее приведены эти формулы для трения на боковой поверхности и осевой жесткости. Также здесь включены рекомендуемые коэффициенты корректировки для ввода в RFEM.
|
|
Модуль сдвига грунта (из отношения модуля Юнга и коэффициента Пуассона; Модуль Юнга для нелинейной модели материалов: простой (например, модель Мора-Кулона) первый подход Eprim или более сложный (например, модель тангенса) Eur~5 x E(50),prim) |
|
Γs |
Коэффициент модификации ствола сваи (эмпирический; рекомендуется: 1) |
|
Δs |
Начальное сопротивление трения корпуса (эмпирическое значение; рекомендуемое значение: 0) |
|
fs,RН |
Fременный фактор RFEM (рекомендуемое значение: 0,1) |
|
G |
Модуль сдвига основания (из коэффициента Пуассона и модуля упругости; модуль упругости для нелинейной модели материала: простой (например, Мора-Кулона) первоначальная нагрузка Eprim или более высокого порядка (например, упрочнённого грунта) Eur~5 x E(50),prim) |
|
Γb |
Коэффициент адаптации для острия сваи (эмпирический; рекомендуется: 5-10) |
|
req |
Эквивалентный радиус наконечника сваи |
|
fb,RF |
Коэффициент адаптации RFEM (рекомендуемое значение: 0,01) |
Через подстановку рекомендуемых значений возможно выполнить ввод трения на боковой поверхности и осевой жесткости через следующие формулы.
|
|
Модуль сдвига грунта (по коэффициенту поперечного деформирования и модулю упругости); модуль упругости для нелинейной модели материала: простой (напр. Моhr-Coulomb) первоначальная нагрузка Eprim или высшего порядка (напр. Hardening-Soil) Eur~5 x E(50),prim) |
|
req |
Эквивалентный радиус конца сваи |