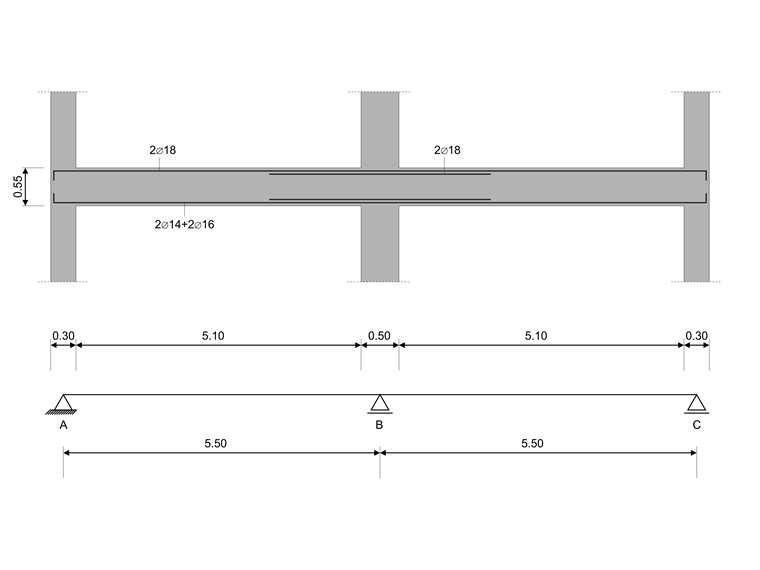
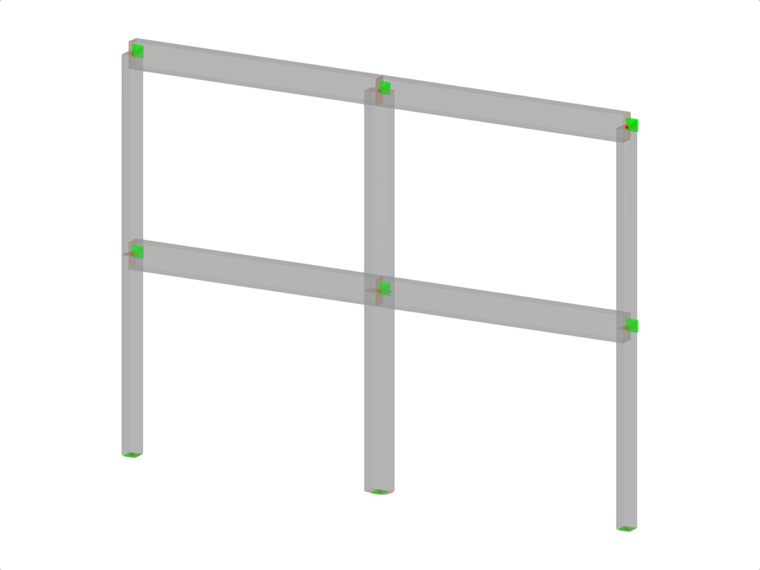
En este ejemplo de verificación, los valores de cálculo de la capacidad de los esfuerzos cortantes en vigas se calculan según EN 1998-1, 5.4.2.2 y 5.5.2.1, así como los valores de cálculo de la capacidad de los pilares en flexión según 5.2.3.3(2 ). El sistema consiste en una viga de hormigón armado de dos vanos con una longitud de vano de 5,50 m. La viga es parte de un sistema de pórtico. Los resultados obtenidos se comparan con los de [1].
| Material | Hormigón C20/25 | Módulo de elasticidad | E | 30000 | N/mm2 |
| Valor de cálculo de la resistencia a compresión del hormigón | fcd | 11,333 | N/mm2 | ||
| Acero de armadura B400S(C) | Módulo de elasticidad | Es | 200000,000 | N/mm2 | |
| Valor de cálculo del límite elástico | fyd | 347,826 | N/mm2 | ||
| Geometría | Estructura | Longitud de las vigas | lb | 5,500 | m |
| Longitud de los pilares | lc | 4,000 | m | ||
| Sección de vigas | Altitud | h | 550 | mm | |
| Ancho | b | 300 | mm | ||
| Recubrimiento de hormigón | cnom | 20 | mm | ||
| Sección de los pilares | Altitud | h | 500 | mm | |
| Ancho | b | 300 | mm | ||
| Recubrimiento de hormigón | cnom | 22 | mm | ||
| Cargas | Cargas permanentes | Carga permanente | CC1 | 10,875 | kN/m |
| Carga permanente | CC1 | 571,900 | kN | ||
| Carga permanente | CC1 | 158,650 | kN | ||
| Sobrecargas de uso | sobrecarga de uso | CC2 | 20,000 | kN/m | |
| Cargas dinámicas | Modal | CC3 | |||
| Espectro de respuesta | CC4 |
Configuración de RFEM
- la clase de ductilidad del modelo se establece en ductilidad alta (DCH)
Resultados
- Regla de capacidad para cortante -Valores de cálculo de capacidad de esfuerzos cortantes en vigas acc. según EN 1998-1, 5.4.2.2 y EN 1998-1, 5.5.2.1
<br/> La regla de cálculo de capacidad de comprobación para cortante se lleva a cabo para la barra 11 en la cara de los apoyos A (x=0,0 m) y B (x=5,1 m).
<br />Regla de capacidad para cortante- Valores de cálculo de capacidad de esfuerzos cortantes en vigas según según EN 1998-1, 5.4.2.2 y EN 1998-1, 5.5.2.1 Parámetro Descripción del trabajo Unidad rfem Solución de referencia Razón M+Rd,1,y Momento resistente (pandeo) positivo al inicio de la barra [kNm] 119,914 118,700 1,01 M-Rd,1,y Momento resistente negativo al inicio de la barra [kNm] -86,529 -85,800 1,01 M+Rd,2,y Momento resistente (pandeo) positivo en el extremo de la barra [kNm] 120,247 118,700 1,01 M-Rd,2,y Momento resistente negativo (carga vertical) en el extremo de la barra [kNm] -170,848 -168,800 1,01 lcl Vano libre de la viga [m] 5.100 5.100 1,00 VA,g+ψ2 q,máx. Esfuerzo cortante debido a cargas cuasipermanentes para una viga simplemente apoyada en la cara del apoyo A [kN] 53,550 53,550 1,00 V-A,Ed,máx.,z Esfuerzo cortante correspondiente al momento extremo negativo máximo en dirección z [kN] -14,878 -14.100 1,06*) V+A,Ed,máx.,z Esfuerzo cortante correspondiente al momento máximo positivo en el extremo en dirección z [kN] 102,213 101,670 1,01 ζ1,máx. Razón entre los esfuerzos cortantes de cálculo V-Ed,máx./V+Ed,máx. [-] -0,146 -0,139 1,05 VB,g+ψ2 q,máx. Esfuerzo cortante debido a cargas cuasipermanentes para una viga simplemente apoyada en la cara del apoyo B [kN] 53,550 53,550 1,00 V-B,Ed,mín.,z Esfuerzo cortante correspondiente al momento extremo negativo mínimo en dirección z [kN] -121,978 -121,200 1,01 V+B,Ed,mín.,z Esfuerzo cortante correspondiente al momento extremo positivo mínimo en dirección z [kN] -4,887 -5.430 0,90*) ζ2,mín. Razón entre los esfuerzos cortantes de cálculo V+Ed,mín/V-Ed,mín [-] -0,040 -0,045 0,90
*) La diferencia absoluta entre esos resultados es menor que 1 kN.
- Regla de capacidad para flexión - Cálculo de capacidad de pilares en flexión acc. según EN 1998-1, 5.2.3.3(2)
<br/> La regla de capacidad de comprobación de cálculo para flexión se lleva a cabo en la cara de los apoyos al inicio de la barra del pilar 5.
Regla de capacidad para flexión - Cálculo de la capacidad de pilares en flexión acc. según EN 1998-1, 5.2.3.3(2) Parámetro Descripción del trabajo Unidad rfem Solución de referencia Razón M+Rd,c,1,y,5 Momento resistente positivo del pilar 5 [kNm] -294.602 -281.000 1,05 M+Rd,c,1,y,2 Momento resistente positivo del pilar 2 [kNm] -300.046 -295.000 1,02 ΣM+Rd,c,1,y Suma de momentos resistentes de pilares en el nudo 1 (nudo inicial) del pilar 5 [kNm] -594.648 -576.000 1,03 M-Rd,b,1,y,11 Momento resistente negativo de la barra 11 (lado izquierdo) del nudo [kNm] -170,848 -168,800 1,01 M-Rd,b,1,y,12 Momento resistente negativo de la barra 12 (lado derecho) del nudo [kNm] -120,866 -118,700 1,02 ΣM-Rd,b,y Suma de momentos resistentes de vigas en el nudo B [kNm] -291.714 -287,500 1,01 η+y Razón de comprobación de cálculo de momentos de capacidad positiva [-] 0,638 0,649 0,98