Análisis de un pilar de hormigón
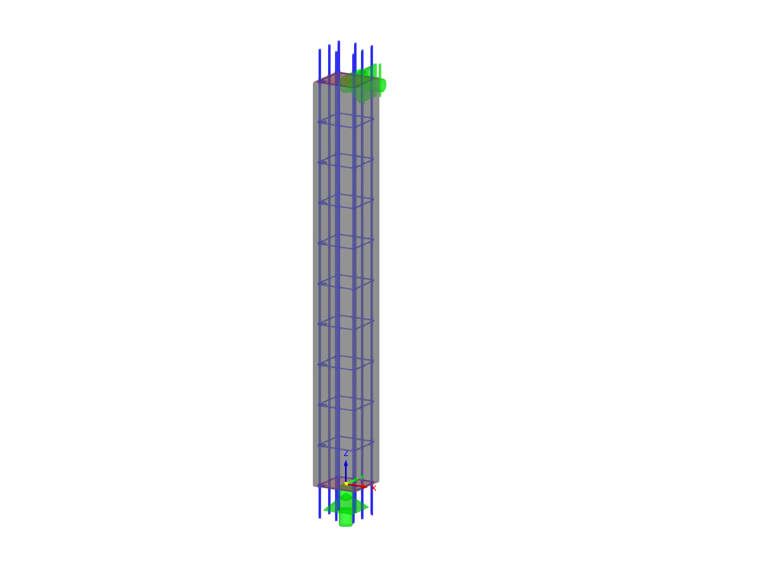
Un pilar de hormigón armado cuadrado con estribos está diseñado para soportar cargas muertas axiales y cargas vivas de 135 y 175 kips, respectivamente, utilizando el cálculo ELU y combinaciones de carga factorizadas LRFD según ACI 318-19 [1] como se presenta en la Imagen 01. El material de hormigón tiene una resistencia a compresión f'c de 4 ksi mientras que el acero de la armadura pasiva tiene un límite elástico fy de 60 ksi. Se supone inicialmente que el porcentaje de la armadura de acero es del 2%.
Cálculo de las dimensiones
Para empezar, se deben calcular las dimensiones de la sección. Se determina que el pilar cuadrado con estribos está controlado a compresión, ya que todas las cargas axiles están estrictamente en compresión. As per Table 21.2.2 [1], the strength reduction factor Φ is equal to 0.65. When determining the maximum axial strength, Table 22.4.2 [1] is referenced, which sets the alpha factor (α) equal to 0.80. Ahora, se puede calcular la carga de cálculo Pu.
Pu = 1,2 (135) + 1,6 (175) = 442 kips
En base a estos factores, Pu es igual a 442 kips. A continuación, se puede calcular la sección bruta Ag utilizando la ecuación 22.4.2.2.
| Φ | Coeficiente de reducción de la resistencia |
| α | Factor alfa |
| f'c | Resistencia a compresión |
| Ast | Porcentaje de armadura de acero |
442 kips = (0.65) (0.80) [0.85 (4 kips) (Ag – 0.02 Ag) + ((60 ksi) (0.02) Ag)]
Resolviendo para Ag, obtenemos un área de 188 in2. Se toma la raíz cuadrada de Ag y se redondea hacia arriba para establecer una sección de 14 x 14 para el pilar.
Armadura de acero necesaria
Now that Ag is established, the steel reinforcement area Ast can be calculated utilizing Eqn. 22.4.2.2 by substituting the known value of Ag = 196 in² and solving it.
442 kips = (0.65) (0.80) [0.85 (4 kips) (196 in² – Ast) + ((60 ksi) (Ast))]
Solving for Ast yields a value of 3.24 in². A partir de esto, se puede obtener el número de barras de la armadura necesarias para el cálculo. According to Section 10.7.3.1 [1], a square tie column is required to have at least four bars. Based on these criteria, and the minimum required area of 3.24 in², (8) No. 6 bars for the steel reinforcement are used from Appendix B [1]. Esto proporciona el área de la armadura siguiente:
Ast = 3.52 in²
Selección de estribos
Determining the minimum tie size requires Section 25.7.2.2 [1]. En la sección anterior, elegimos 6 barras longitudinales Núm. 6 que son más pequeñas que las barras Núm. 10. Según esta información y esta sección, seleccionamos el Núm. 3 para los estribos.
Separación de estribos
To determine the minimum tie spacing(s), we refer to Section 25.7.2.1 [1]. Los estribos que se compongan de barras corrugadas cerradas deben tener una separación que esté de acuerdo con (a) y (b) de esta sección.
(a) La separación libre debe ser al menos (4/3) dagg. Para este cálculo, asumiremos un diámetro agregado (dagg) de 1,00 in.
smín = (4/3) dagg = (4/3) (1,00 in) = 1,33 in (pulgadas)
(b) La distancia de centro a centro no debe exceder el mínimo de 16 db del diámetro de la barra longitudinal, 48 db de la barra del estribo o la dimensión mínima de la barra.
sMáx = Mín. (16 db, 48 db, 14 in)
16 db = 16 (0,75 in) = 12 in
48 db = 48 (0,375 in) = 18 in
El espacio libre mínimo de los tirantes calculado es igual a 1,33 in y el espacio máximo de los tirantes calculado es igual a 12 in. Para este diseño, regirá un máximo de 12 in para el espaciado de los tirantes.
Comprobación de los detalles
La comprobación de los detalles se puede realizar ahora para comprobar el porcentaje de la armadura. The required steel percentage must be between 1% and 8%, based on the ACI 318-19 [1] requirements, to be adequate.
| Ast | Área total de armadura longitudinal sin pretensar incluyendo barras o perfiles de acero y excluyendo la armadura de pretensado |
| Ag | Sección bruta |
Separación entre barras en dirección longitudinal
La separación máxima entre barras en dirección longitudinal se puede calcular basándose en la separación del recubrimiento libre y el diámetro de las barras tanto de los estribos como longitudinales.
4.00 inches are less than 6 inches, which are required as per 25.7.2.3 (a) [1].
The minimum longitudinal bar spacing can be calculated by referencing 25.2.3 [1], which states that the minimum longitudinal spacing for columns must be at least the greatest of (a) through (c).
(a) 1,5 in
(b) 1,5 db = 1,5 (0,75 in) = 1,125 in
(c) (4/3) db = (4/3) (1,00 in) = 1,33 in
Por lo tanto, la separación mínima de las barras longitudinales es de 1,50 in.
The development length (Ld) must also be calculated with reference to 25.4.9.2 [1]. Este será igual al mayor de (a) o (b) calculado a continuación.
| fy | Límite elástico especificado para la armadura sin pretensar |
| ψr | Coeficiente utilizado para modificar la longitud de desarrollo basada en la armadura de confinamiento |
| λ | Coeficiente de modificación para reflejar las propiedades mecánicas reducidas del hormigón ligero en relación con el hormigón de peso normal de la misma resistencia a compresión |
| f'c | Resistencia a compresión |
| db | Diámetro nominal de la barra, alambre o cordón de pretensado |
| fy | Límite elástico especificado para la armadura sin pretensar |
| ψr | Coeficiente utilizado para modificar la longitud de desarrollo basada en la armadura de confinamiento |
| db | Diámetro nominal de la barra, alambre o cordón de pretensado |
En este ejemplo, (a) es el valor mayor, por lo que Ldc = 14,23 in.
Referencing 25.4.10.1 [1], the development length is multiplied by the ratio of the required steel reinforcement over provided steel reinforcement.
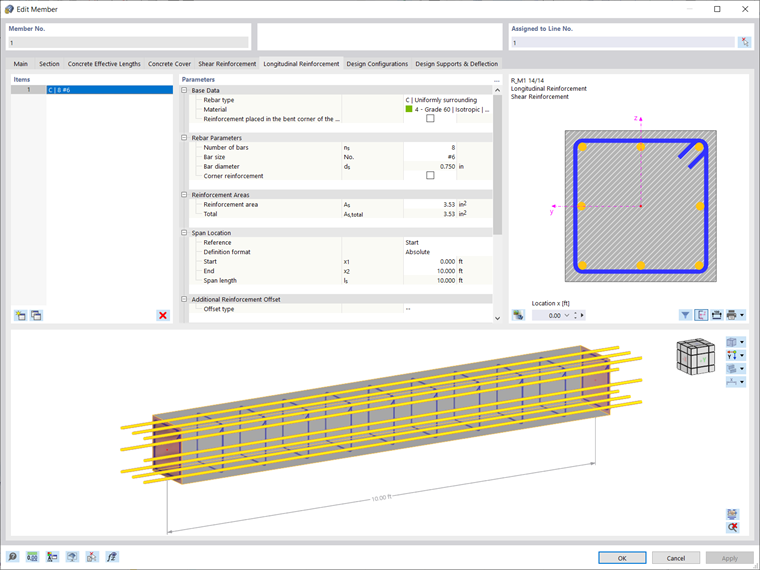
The reinforced square tie column is fully designed, and its cross-section can be viewed below in Image 02.
Comparación con RFEM
An alternative to designing a square tie column manually is utilizing the Concrete Design add-on in RFEM 6 and performing the design as per the ACI 318-19 [1] standard. El complemento determinará la armadura necesaria para resistir las cargas aplicadas en el pilar. Luego, se requiere que el usuario realice ajustes manualmente en la disposición de la armadura proporcionada para cumplir con la armadura necesaria que se muestra.
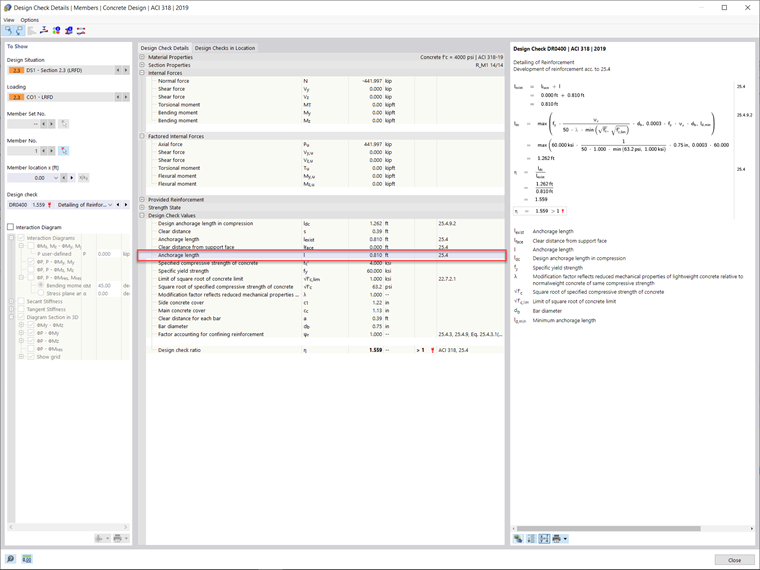
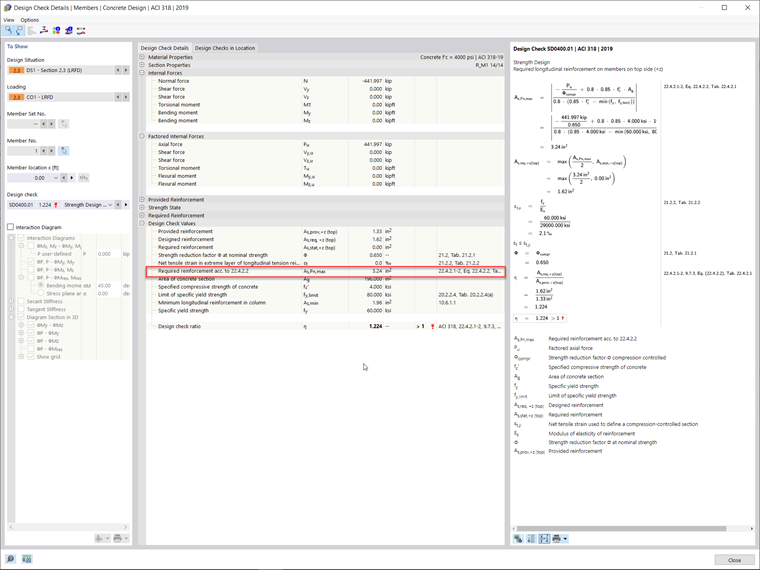
Based on the applied loads for this example, RFEM 6 has determined a required longitudinal bar reinforcement area of 3.24 in². La longitud de desarrollo calculada en el complemento Cálculo de hormigón es igual a 0,81 ft (pies). The discrepancy in comparison to the development length above, calculated with analytical equations, is due to the program's non-linear calculations, including the partial factor γ. El coeficiente γ es la relación entre los esfuerzos internos últimos y los actuantes tomados de RFEM. The development length in the Concrete Design add-on is found by multiplying the reciprocal value of gamma by the length determined from 25.4.9.2 [1]. This development length and reinforcement can be previewed in Image 03 and Image 04, respectively.
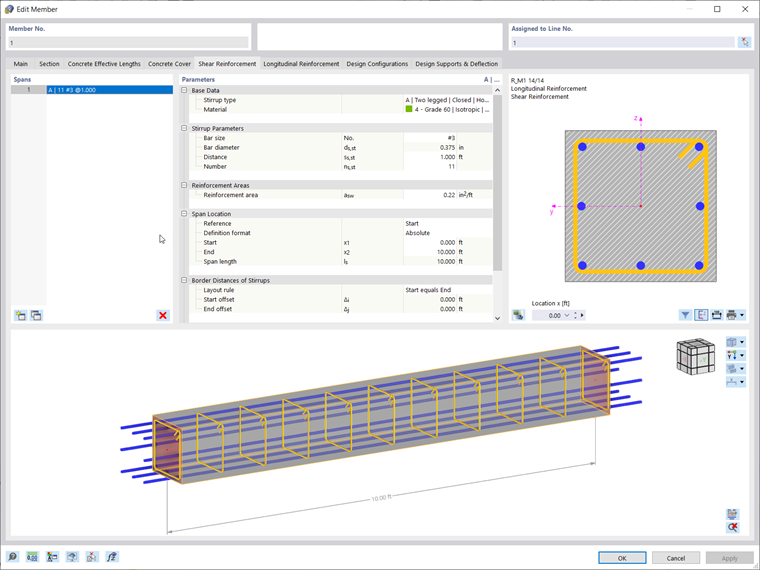
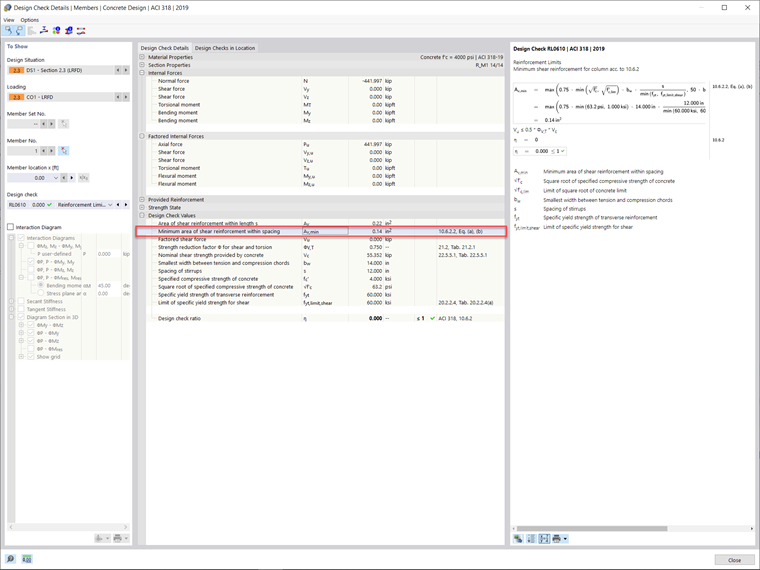
The minimum required shear reinforcement area (Av,min) for the member within the Concrete Design add-on was calculated to be 0.14 in² bars with a minimum spacing (smax) of 12 inches. The required shear reinforcement layout is shown below in Image 05.
