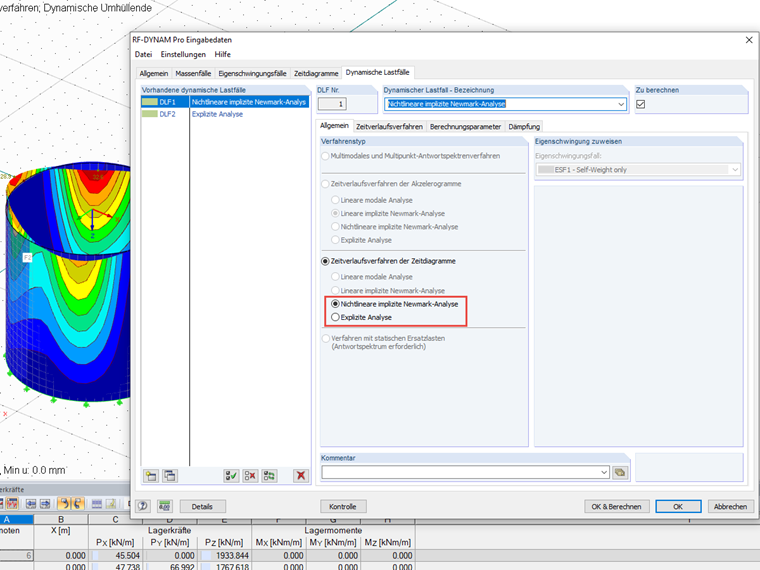
En el módulo adicional RF-DYNAM Pro - Nonlinear Time History Analysis, están disponibles dos métodos diferentes para el análisis dinámico no lineal: die explizite Zentrale Differenzenmethode und die implizite Newmark-Analyse der mittleren Beschleunigung.
Nichtlineare implizite Newmark-Analyse
Die nichtlineare Newmark-Analyse ist ein implizites Verfahren, welches unbekannte Werte zu der Zeit i+1 bezogen auf die Werte der Zeit i und i+1 löst. Diese Methode ist numerisch unbedingt stabil, unabhängig davon, welche Zeitschrittlänge gewählt wurde. Dies ist ein Grund dafür, dass diese Methode für dynamische Beanspruchungen, welche über einen längeren Zeitraum wirken, meistens zu bevorzugen ist.
Análisis explícito
Die explizite Analyse ist eindeutig, weil sie Werte unabhängig von den unbekannten Werten zu der Zeit i+1 löst. Dies ist jedoch ein Grund dafür, dass die explizite Analyse nur dann stabil ist, wenn der gewählte Zeitschritt kleiner ist als ein bestimmter, kritischer Zeitschritt. Die Berechnungszeit eines einzelnen Zeitschritts ist sehr kurz, jedoch können unzählige, sehr feine Zeitschritte notwendig sein, um überhaupt ein Ergebnis zu erhalten.
Der explizite Löser ist deshalb dann zu bevorzugen, wenn man ohnehin sehr feine Zeitschritte wählen muss, um ein brauchbares (konvergierendes) Ergebnis zu erhalten. Dies ist beispielsweise bei sehr kurzzeitig wirkenden und sprunghaft veränderlichen Beanspruchungen, wie Anprall- oder Explosionslasten, der Fall.
Conclusión
Zusammenfassend ist zu sagen, dass im nichtlinearen Bereich beide Verfahren „nur" numerisch bedingt stabil sind, wobei immer noch gilt, dass die implizite Newmark-Analyse in den meisten Fällen stabiler ist als die Zentrale Differenzenmethode.
Es ist jedoch zu beachten, dass auch bei der Newmark-Analyse auf einen ausreichend kleinen Zeitschritt geachtet werden muss, um exakte Ergebnisse zu erzielen. Welcher Zeitschritt in einer dynamischen Berechnung gewählt werden sollte, wird in FAQ 2655 ausführlich erläutert.
Nähere Informationen, insbesondere zu dem kritischen Zeitschritt in der expliziten Analyse, sind im Handbuch von RF-DYNAM Pro zu finden.