Réponse:
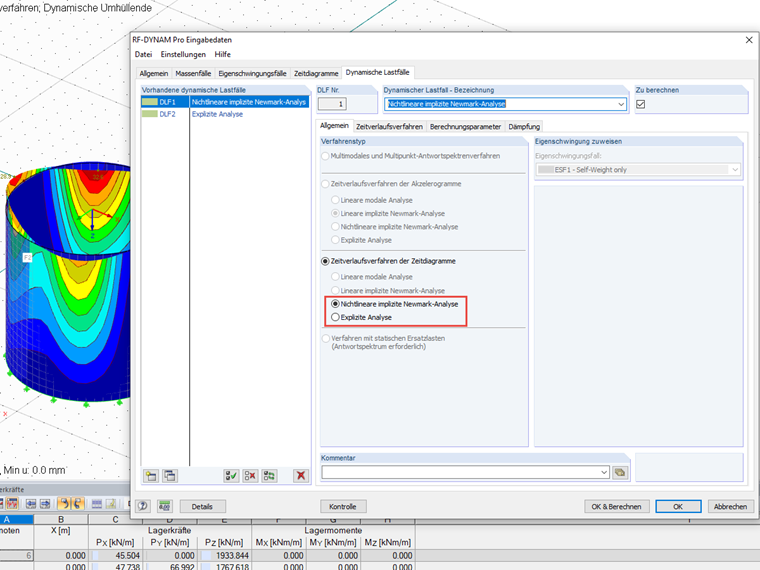
Dans le module additionnel RF-DYNAM Pro - Nonlinear Time History Analysis, deux méthodes différentes sont disponibles pour l’analyse dynamique non linéaire : la méthode explicite des différences centrales et l’analyse implicite de Newmark de l’accélération moyenne.
Nichtlineare implizite Newmark-Analyse
L’analyse non linéaire de Newmark est une méthode implicite qui résout les valeurs inconnues au temps i+1 par rapport aux valeurs au temps i et i+1. Cette méthode est numériquement stable, quel que soit le pas de temps sélectionné. C'est l’une des raisons pour lesquelles cette méthode est généralement préférée pour les charges dynamiques agissant sur une longue période.
Analyse explicite
L’analyse explicite est claire car elle résout les valeurs indépendamment des valeurs inconnues à l’instant i+1. Cependant, c'est la raison pour laquelle l’analyse explicite n’est stable que si le pas de temps sélectionné est inférieur à un certain pas de temps critique. Le temps de calcul d’un pas de temps est très court, mais de nombreux pas de temps très fins peuvent être nécessaires pour obtenir un résultat.
Par conséquent, le solveur explicite est préférable si vous devez sélectionner des pas de temps très fins afin d’obtenir un résultat utile (convergent). C'est le cas, par exemple, pour les charges à très court terme et brusquement variables, telles que les charges d’impact ou les charges d’explosion.
Conclusion
En résumé, les deux méthodes ne sont « numériquement » stables que dans le domaine non linéaire, tandis que l’analyse implicite de Newmark est toujours plus stable que la méthode des différences centrales dans la plupart des cas.
Cependant, il convient de noter que dans le cas d’une analyse Newmark, il est nécessaire de faire attention à un pas de temps suffisamment petit pour obtenir des résultats exacts. Le pas de temps à sélectionner pour une analyse dynamique est détaillé dans la FAQ 2655.
De plus amples informations, notamment sur le pas de temps critique dans l’analyse explicite, sont disponibles dans le manuel de RF-DYNAM Pro.
