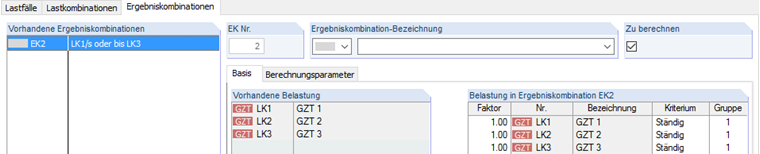
Base de la définition
Une combinaison de cas de charge à l'aide de combinaisons de résultats permet une addition simple et une comparaison des résultats (soit/ou). Par conséquent, la définition des combinaisons de résultats est plus complexe que la définition des combinaisons de charges et dépend en grande partie du «facteur», du «critère» et du «groupe».
«Facteur» multiplie les résultats des cas de charge. Un facteur partiel ou un facteur de combinaison est généralement défini ici. Les valeurs positives signifient addition, les valeurs négatives signifient soustraction.
Le «Critère» détermine si les résultats d'un cas de charge sont toujours appliqués dans la combinaison («Permanent») ou s'ils ont uniquement un effet occasionnel («Variable»). Ainsi, les résultats d'un cas de charge avec le critère «Variable» ne sont considérés dans la superposition que s'ils apportent une contribution défavorable au résultat. Ces deux valeurs sont enregistrées car il n'est pas clair si la valeur maximale positive ou négative maximale contribue au résultat défavorable.
«Groupe» vous permet de définir des actions alternatives pour les cas de charge. Par exemple, si deux cas de charge sont assignés au même groupe, les résultats du premier ou du second cas de charge seront pris en compte dans la combinaison.
Dans les deux exemples suivants, des combinaisons de résultats sont utilisées pour additionner les résultats (exemple 1) et pour trouver le maximum et le minimum de plusieurs situations de charge avec des actions alternatives (exemple 2).
Exemple 1 : Ajout des résultats
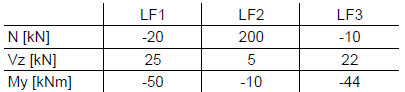
Trois cas de charge différents sont générés sur le même emplacement x dans le modèle. Seuls l'effort normal N, l'effort tranchant Vz et le moment fléchissant My sont considérés de manière simplifiée. Le cas de charge 1 inclut les charges permanentes, les deux autres cas de charge imposés.
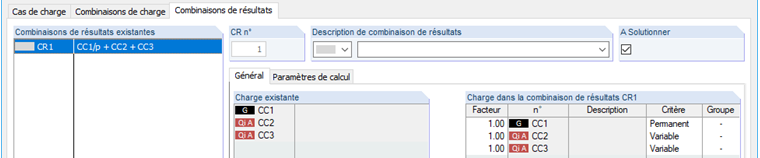
À l'aide de la combinaison de résultats, les trois cas de charge sont maintenant additionnés. Les cas de charge sont définis comme suit:
Le cas de charge 1 incluant les charges permanentes, le critère «Permanent» lui est assigné. Les cas de charge imposés peuvent agir mais pas nécessairement. Par conséquent, ce critère est défini sur «Variable». De même, les deux cas de charge imposés peuvent se produire simultanément. Ainsi, le groupe n'est pas défini. Pour simplifier le recalcul théorique, aucun facteur partiel n'est appliqué (facteur = 1,0).
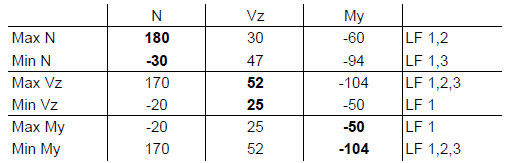
Vous obtenez ainsi une valeur maximale et une valeur minimale pour chaque effort interne. De même, les efforts internes correspondants sont affichés.
Expliquons les résultats plus en détail dans le calcul des N valeurs max. De la première ligne. Dans ce cas, la base de calcul est le cas de charge 1 car il a été défini comme une action «Permanente». Les forces normales des deux autres cas de charge ne sont utilisées que si elles augmentent la force normale. Le cas de charge 2 augmente la force normale maximale alors que le cas de charge 3 la réduit à nouveau. Par conséquent, seuls les cas de charge 1 et 2 s'appliquent à l'effort normal maximal:
Max. N = -20 + 200 = 180 kN
Les efforts internes correspondants doivent être calculés à l'aide de la même combinaison:
Rel. Vz = 25 + 5 = 30 kN
Rel. My = -50 + (-10) = -60 kNm
Les lignes suivantes sont calculées de la même manière et les valeurs maximales et minimales de chaque effort interne, y compris les valeurs associées, sont obtenues. Celles-ci peuvent désormais être utilisées pour des vérifications ultérieures.
Exemple 2 : Enveloppe de résultats des situations de charge avec actions alternatives
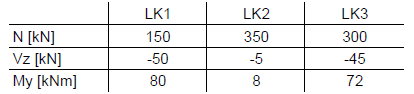
Les résultats de trois combinaisons de charges sont calculés dans le deuxième exemple. Celles-ci ne peuvent pas être combinées, bien sûr, mais il est possible de comparer les unes avec les autres. L'objectif est d'obtenir les forces maximales et minimales de la même manière que dans le premier exemple. Les valeurs suivantes sont disponibles:
La combinaison de résultats est définie comme suit:
Les résultats des combinaisons de charges incluent déjà presque tous les coefficients partiels de sécurité et coefficients de combinaison. Ainsi, le facteur reste 1,0. Pour effectuer cette analyse alternative, chaque combinaison de charges doit avoir le même numéro de groupe. De cette manière, le résultat de CO1, CO2 ou CO3 est enregistré. Il est également important d'assigner le critère «Permanent» à toutes les combinaisons. C'est-à-dire qu'un résultat de trois combinaisons doit toujours être utilisé. Si le critère «Permanent» est assigné à toutes les combinaisons, la force normale minimale ne sera pas de 150 kN, mais de 0 kN. Dans ce cas, l'effort normal est nul si aucune des trois combinaisons de charges n'agit. Les efforts internes maximaux et minimaux sont affichés dans le tableau suivant:
La première ligne sera à nouveau expliquée pour plus de précision. Nous recherchons la force normale maximale. Celles-ci se trouvent dans le CO2 à 350 kN. Pour obtenir Vz et My , il suffit d'adopter les efforts internes correspondants issus du CO2. Ainsi, la résultante Vz est de -5 kN et My de 8 kNm. Ces résultats peuvent être utilisés pour la vérification dans les modules additionnels.
Conclusion
Cet article décrit les principes de base de la définition des combinaisons de résultats et décrit les applications les plus courantes dans un exemple. Il est bien sûr possible de combiner ces procédures de définition. Cette opération est expliquée dans la partie 2 de cette série d'articles avec la comparaison des combinaisons de charges.