Kombinace výsledků 1 | Základy

Základní pravidla zadání

Kombinace výsledků umožňuje kromě prostého sčítání výsledků zatěžovacích stavů také jejich porovnávání (buď/anebo). Jejich zadání je tudíž o něco složitější než v případě kombinací zatížení a rozhodující je pro ně stanovení „součinitele“, „kritéria“ a „skupiny“.

01 - Kombinace výsledků

„Součinitelem“ se násobí výsledky zatěžovacích stavů. Obvykle se zde zadává dílčí součinitel spolehlivosti nebo kombinační součinitel. Kladné hodnoty znamenají přičítání, záporné pak odečítání.

„Kritérium“ stanoví, zda se mají výsledky zatěžovacího stavu uvažovat v kombinaci vždy („stálé“) nebo pouze v určitém případě („proměnné“). Výsledky zatěžovacího stavu se zadaným kritériem „proměnné“ vstupují do kombinace pouze v případě, že nepříznivě ovlivňují výsledek. Protože není jasné, zda k nejméně příznivému výsledku přispěje maximální kladná nebo maximální záporná hodnota, zaznamenávají se obě hodnoty.

„Skupina“ umožňuje nastavit alternativní působení určitých zatěžovacích stavů. Pokud například zařadíme dva zatěžovací stavy do stejné skupiny, zahrnou se do kombinace pouze výsledky prvního anebo druhého zatěžovacího stavu.

Níže si v prvním příkladu kombinace výsledků předvedeme sčítání výsledků a v druhém příkladu pak hledání maximálních a minimálních hodnot několika alternativně působících zatěžovacích situací.

Příklad 1: Sčítání výsledků

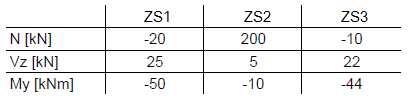
V našem příkladu jsou dány výsledky tří různých zatěžovacích stavů na stejném místě x v konstrukci. Pro zjednodušení budeme uvažovat pouze normálovou sílu N, posouvající sílu V_z a ohybový moment M_y. Zatěžovací stav 1 obsahuje stálá zatížení, ostatní dva zatěžovací stavy představují užitná zatížení.

02 - Vnitřní síly po zatěžovacích stavech

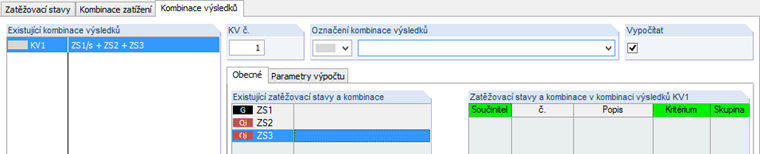
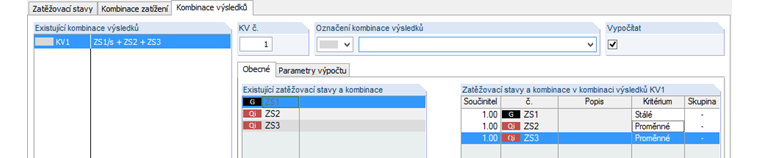
Pomocí kombinace výsledků nyní všechny tři zatěžovací stavy sečteme. Kombinaci zadáme následovně:

3 - Addition mittels Ergebniskombination

Zatěžovací stav 1 obsahuje stálá zatížení, proto vstupuje do kombinace s kritériem „stálé“. Užitná zatížení mohou, ale také nemusí působit. Proto u daných zatěžovacích stavů nastavíme kritérium „proměnné“. Užitná zatížení z těchto zatěžovacích stavů se mohou vyskytovat také současně. Proto nezadáme žádnou skupinu. Abychom si mohli výsledek snáze přepočítat, nezadáme žádné dílčí součinitele spolehlivosti (součinitel = 1,0).

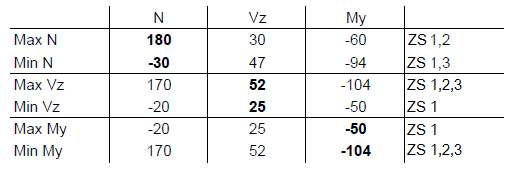
Výsledkem je pro každou vnitřní sílu její maximální a minimální hodnota. Zobrazí se vždy i příslušné vnitřní síly.

4 - Výsledná kombinace výsledků

Pro bližší vysvětlení si ukážeme výpočet hodnot z prvního řádku Max N. Základ pro výpočet tu představuje zatěžovací stav 1, protože jeho působení jsme zadali jako „stálé“. Normálové síly ostatních dvou zatěžovacích stavů se mají uvažovat pouze v případě, že přispívají ke zvýšení dané normálové síly. Zatěžovací stav 2 zvyšuje maximální normálovou sílu, zatímco zatěžovací stav 3 ji zase naopak snižuje. Pro maximální normálovou sílu se tak mají uvažovat pouze zatěžovací stavy 1 a 2:
Max. N = -20 + 200 = 180 kN

Příslušné vnitřní síly je třeba spočítat pomocí stejné kombinace:
Přísl. V_z = 25 + 5 = 30 kN
Přísl. M_y = -50 + (-10) = -60 kNm

Stejným způsobem se spočítají ostatní řádky a pro každou vnitřní sílu dostaneme její maximální a minimální hodnotu včetně příslušných hodnot ostatních vnitřních sil, které lze použít pro další posouzení.

Příklad 2: Obálka výsledků alternativních zatěžovacích situací

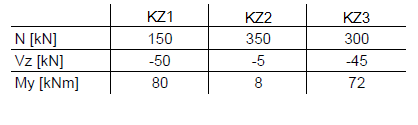
V druhém příkladu máme výsledky tří kombinací zatížení (KZ). Nebudeme je samozřejmě sčítat do kombinace, ale porovnáme je jako alternativní. Cílem je stanovit maximální a minimální vnitřní síly podobně jako v prvním příkladu. Máme následující hodnoty:

05 - Vnitřní síly po zatěžovacích stavech

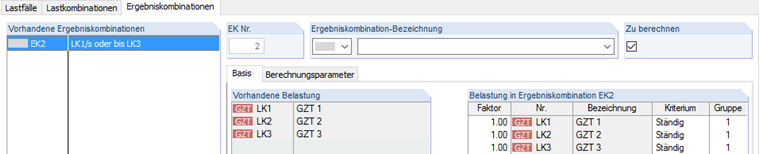
Kombinaci výsledků zadáme následovně:

06 - Kombinace výsledků jako obálka alternativně působících zatěžovacích situací

Ve výsledcích kombinací zatížení jsou již obvykle obsaženy všechny dílčí součinitele spolehlivosti a kombinační součinitele. Proto ponecháme hodnotu součinitele 1,0. Pokud se má provést analýza alternativně, je třeba každé kombinaci zatížení přiřadit stejné číslo skupiny. Bude se tak uvažovat buď výsledek z KZ1 nebo z KZ2 nebo z KZ3. Důležité je také přiřadit všem kombinacím zatížení kritérium „stálé“. To znamená, že se vždy musí zohlednit některý výsledek z daných tří kombinací. Pokud bychom všem kombinacím zatížení přiřadili kritérium „proměnné“, činila by minimální normálová síla nikoli 150 kN, nýbrž 0 kN. V takovém případě je normálová síla nulová, pokud nepůsobí žádná z daných tří kombinací zatížení. Maximální a minimální vnitřní síly uvádíme v následující tabulce:

07 - Výsledek kombinace výsledků

Pro vysvětlení se opět blíže podíváme na první řádek. V daném případě se hledá maximální normálová síla. Najdeme ji v KZ2, kdy dosahuje 350 kN. Pro V_z a M_y je nyní ještě třeba převzít příslušné vnitřní síly z KZ2. V_z tak má hodnotu -5 kN a M_y 8 kNm. Také tyto výsledky můžeme následně použít pro posouzení v přídavných modulech.

Shrnutí

V našem příspěvku jsme vysvětlili základní pravidla zadání kombinací výsledků a jejich nejběžnější použití jsme si předvedli na příkladech. Uživatel má samozřejmě možnost oba způsoby zadání sloučit, což si předvedeme v našem následujícím příspěvku. V něm také kombinace výsledků porovnáme s kombinacemi zatížení.

Literatura