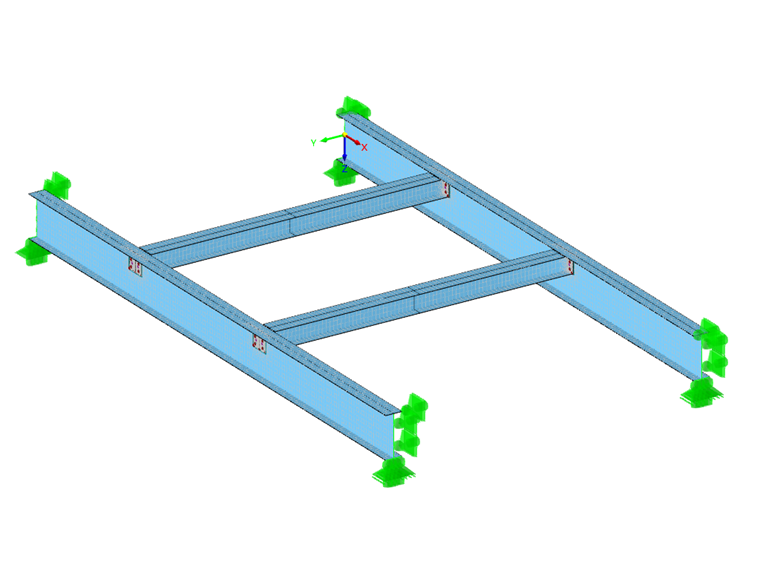
Sistema estructural
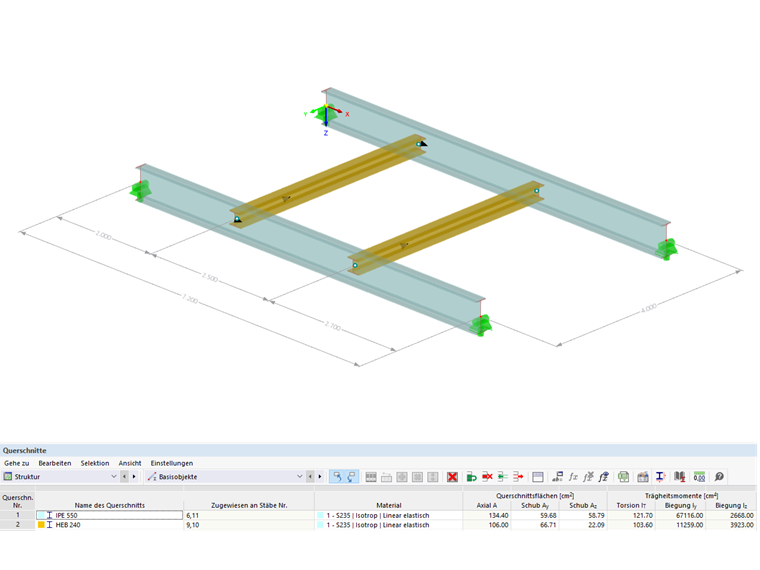
Secciones :
Vigas principales = IPE 550
Vigas secundarias = HE-B 240
Material :
Acero estructural S235 según DIN EN 1993-1-1, tabla 3.1
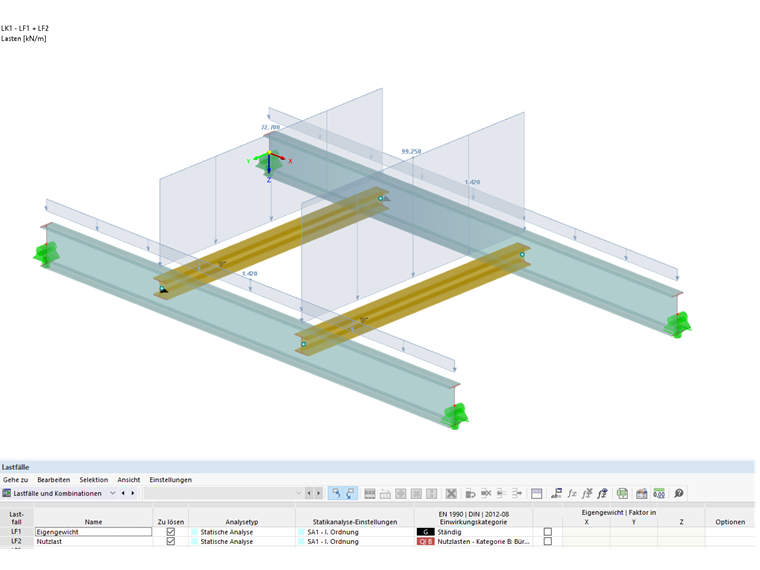
Cargas de cálculo
CC 1 Peso propio:
gd = 1,42 kN/m
CC 2 sobrecarga de uso:
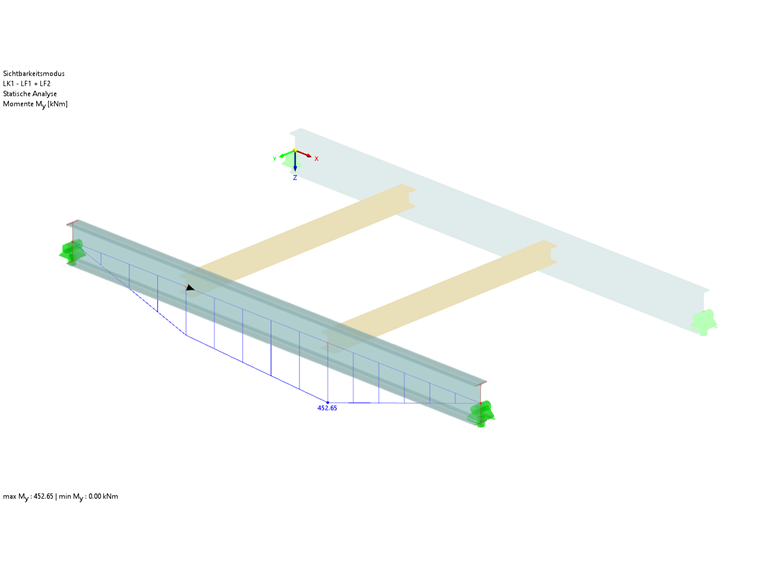
esfuerzos internos de cálculo
Análisis de estabilidad sin considerar las vigas secundarias según el apartado 6.3.2 de EN 1993-1-1
Bajo el supuesto de una coacción lateral y torsional disponible en el inicio y final de la barra, se determinó un momento crítico ideal para el pandeo lateralMcr de 365 kNm. Por lo tanto, el cálculo según la ecuación 6.55 da como resultado 1.65. Por lo tanto, el cálculo del estado límite último no se puede cumplir sin el efecto estabilizador de las vigas secundarias.
Análisis de estabilidad considerando vigas secundarias según EN 1993-1-1, anexo BB.2.2
Las reglas de DIN EN 1993-1-1, anexo BB.2.2 asumen una coacción al giro continua sobre la longitud de la viga. Por lo tanto, la coacción al giro discreta disponible en el modelo se "derrama" en una coacción al giro continua.
Determinación de la coacción al giro continua disponible:
Los valores se toman de [2] y se ajustan a la notación del anexo BB.2.2.
Cθ, R, k = 11,823 kNm (componente de la deformación por flexión de los travesaños)
Cθ, D, k = 359 kNm (componente de la deformación de la sección de la viga principal, teniendo en cuenta la unión en el alma)
Conversión a una coacción al giro continua Cθ basada en las vigas secundarias con la distancia media de las vigas secundarias:
Determinación de la coacción al giro necesaria:
donde:
Kυ = 0,35 para la utilización de la sección elástica
Kθ = 10 según DIN EN 1993-1-1/NA, tabla BB.1
Es posible una reducción de Cθ,mín por (MEd/Mel,Rd )²:
El cálculo:
Cθ,vorh = 134 kNm/m < Cθ,min = 200,9 kNm/m
No se puede realizar el cálculo en forma de verificación de una coacción suficiente para la deformación lateral de la viga principal según el anexo BB.2.2.
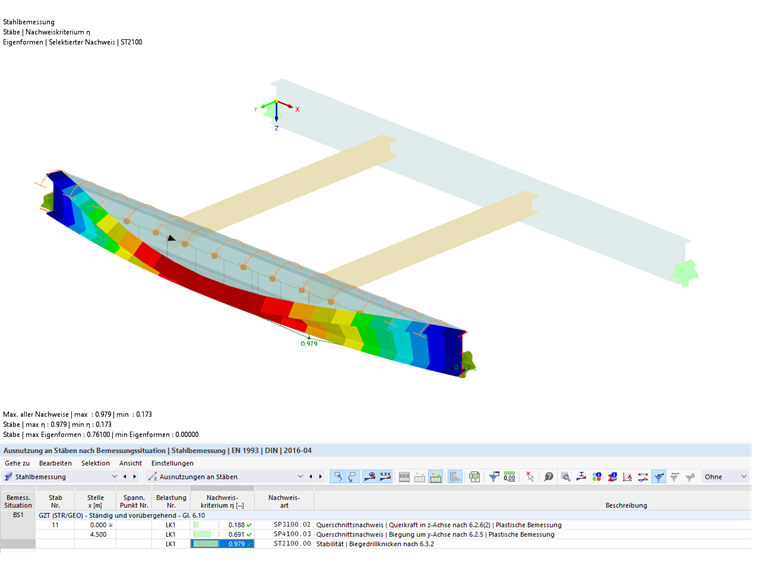
Análisis de estabilidad considerando vigas secundarias según EN 1993-1-1, apartado 6.3.2, con coacción al giro continua
Dado que no se pudo realizar el cálculo de una coacción lateral suficiente según el anexo BB.2.2, la coacción al giro existente se integra aún más en el cálculo del sistema estructural según el apartado 6.3.2 para comprobar si es suficiente.
Debido a la rigidez elástica a torsión continua aplicada de Cθ, prov = 134 kNm/m, el momento de pandeo lateral idealizado se incrementa a Mcr = 982 kNm. Resulta de la multiplicación con el momento flector de cálculo y el amplificador αcr, con el cual se alcanza la carga crítica elástica mínima de pandeo con deformaciones desde el plano del sistema estructural. El factor acr es 2,169 debido a la coacción al giro continua. Por lo tanto, la aplicación de una coacción al giro tiene un efecto favorable en el cálculo, por lo que el cálculo según la ecuación 6.55 es finalmente 0,979.
Análisis de estabilidad considerando vigas secundarias según EN 1993-1-1, apartado 6.3.2, con coacción al giro discreta
A continuación, se analizará la aplicación de una coacción al giro discreta.
Determinación de la coacción al giro discreta disponible:
Los valores se toman de [2] y se ajustan a la notación del anexo BB.2.2.
Cθ, R, k = 11,823 kNm (componente de la deformación por flexión de los travesaños)
Cθ, D, k = 359 kNm (componente de la deformación de la sección de la viga principal, teniendo en cuenta la unión en el alma)
Para el cálculo según 6.3.2, se determina un amplificador de αcr = 2.196 con la coacción al giro discreta. El resultado es un momentoMcr de 452,65 kNm ∙ 2,196 = 994,09 kNm.
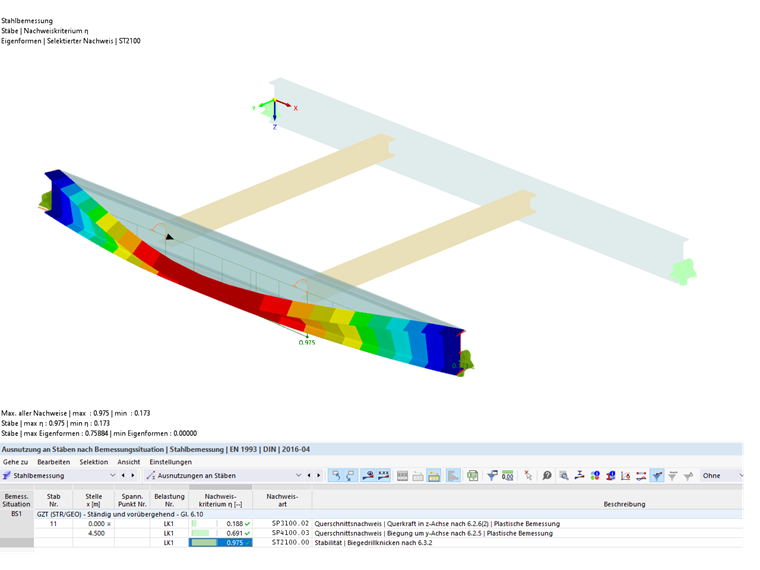
El cálculo según la ecuación 6.55 da como resultado 0,975 para el sistema estructural.
Análisis de estabilidad considerando vigas secundarias según el análisis de segundo orden con 7 GDL (torsión de alabeo)
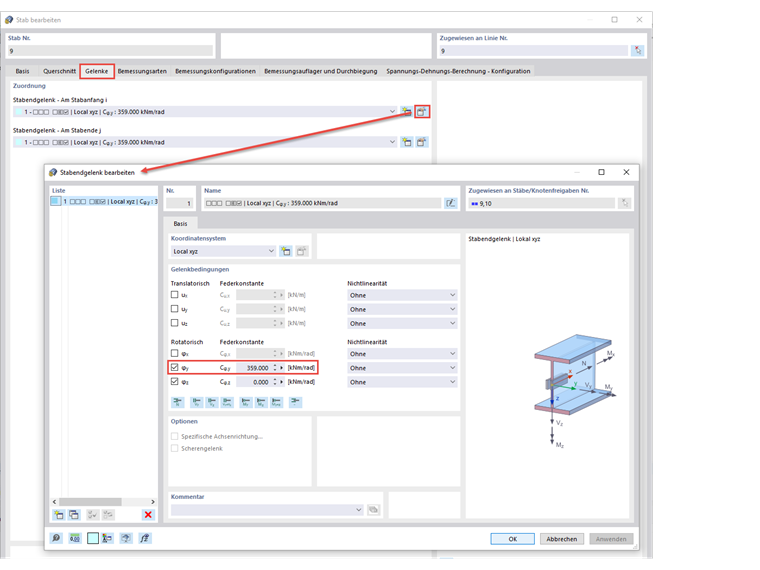
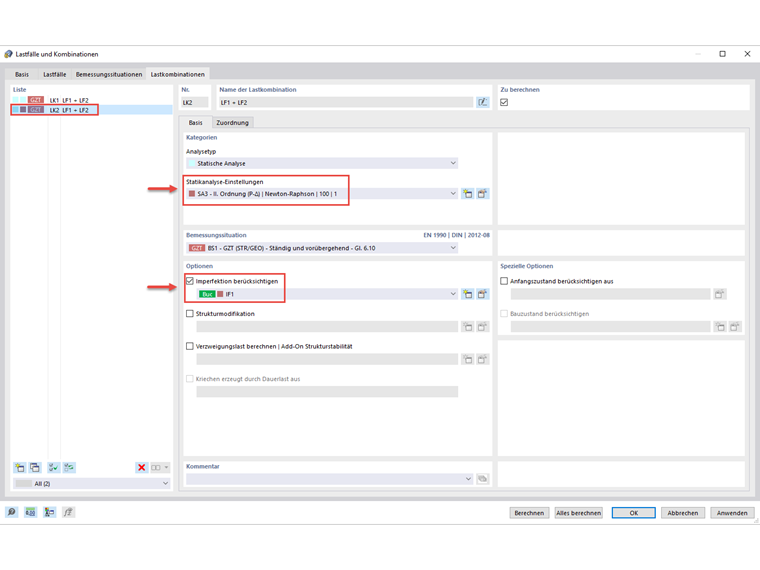
Para este cálculo, es necesario activar los complementos "Estabilidad de la estructura" y "Alabeo por torsión" en los Datos básicos. Además, es importante desactivar el análisis de estabilidad en las configuraciones de cálculo, ya que las comprobaciones de diseño se deben realizar en forma de comprobaciones de diseño de la sección según el análisis de segundo orden, teniendo en cuenta la imperfección y aplicando γm1. Posteriormente, se modifican las articulaciones de las barras de las vigas secundarias.
Al determinar la coacción al giro discreta existente, se omite el componente de la deformación por flexión de las vigas secundarias Cθ,R,k, porque la interacción de las vigas principal y secundaria ya está incluida en el modelo con 7 grados de libertad. Por lo tanto, solo es necesario considerar el muelle de la deformación de la sección de la viga principal conCθ,D,k = 359 kNm. Esta constante elástica se usa para modificar las articulaciones de las barras de las vigas secundarias. Además, se debe asegurar que todas las cargas actuantes se apliquen en el borde superior de la sección o en una posición excéntrica desfavorable.
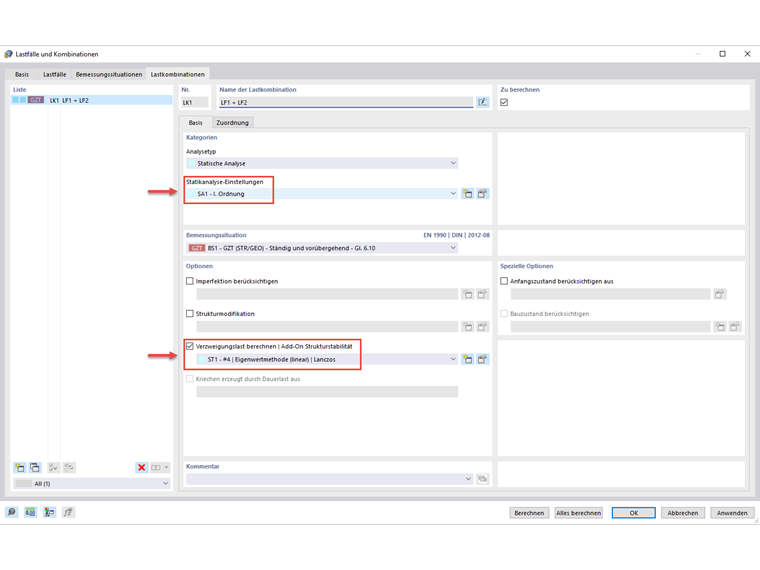
Dado que el cálculo se realiza según el análisis de segundo orden, también es necesario considerar las imperfecciones. Esto se hace determinando la forma de pandeo o pandeo lateral utilizando el complemento "Estabilidad estructural". Para esto, la combinación de carga aplicada (aquí: CO1) calcula la carga crítica según el análisis estático lineal y luego genera la imperfección sobre la base de la deformada del modo resultante.
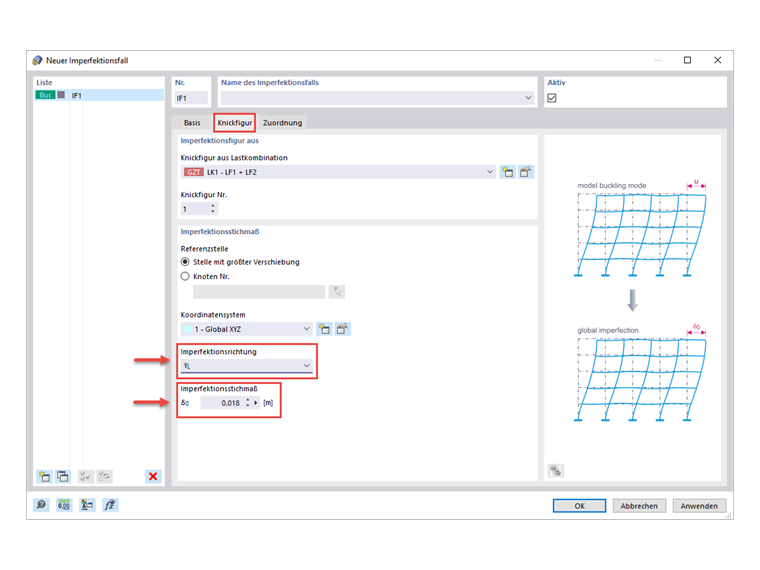
Para crear esta imperfección, primero es necesario crear un nuevo caso de imperfección, que se basa en la forma de pandeo debido a la combinación de carga. Entre otras cosas, se debe especificar una magnitud de imperfección, que resulta de la multiplicación de la relación de cálculo de la sección e0/L y la longitud L de la sección. La relación de la sección depende del tipo y las dimensiones de la sección. Dado que las vigas principales del modelo consisten en secciones laminadas en I con las dimensiones h/b > 2, se aplica la relación de secciones e0/L = 1/400. Con la longitud de la sección de L = 7,20 m, la dimensión de la imperfección resultante es finalmente de 0,018 m en la dirección y.
Ahora, es necesario asignar este caso de imperfección a la combinación de cargas. Para evitar una referencia circular, se crea una nueva combinación de carga copiando el CO en el que se basa la imperfección y calculándolo según el análisis de segundo orden.
Al realizar el cálculo de la estructura de acero, el cálculo de la sección ahora se realiza según el análisis de segundo orden, teniendo en cuenta la imperfección. Basándose en los esfuerzos internos determinados, finalmente se obtiene la razón de tensiones de 0,987 según la ecuación 6.1.
Verificación de la corrección del cálculo utilizando el modelo de análisis por elementos finitos
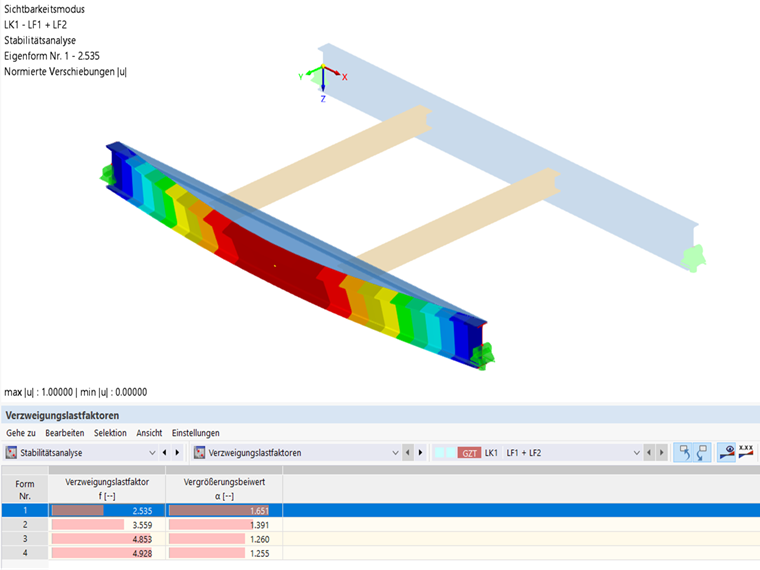
Durante el análisis de estabilidad de CO1 en el modelo con 7 grados de libertad, se utilizó un factor de carga crítica de 2,535, que se debe validar posteriormente utilizando un modelo por el MEF.
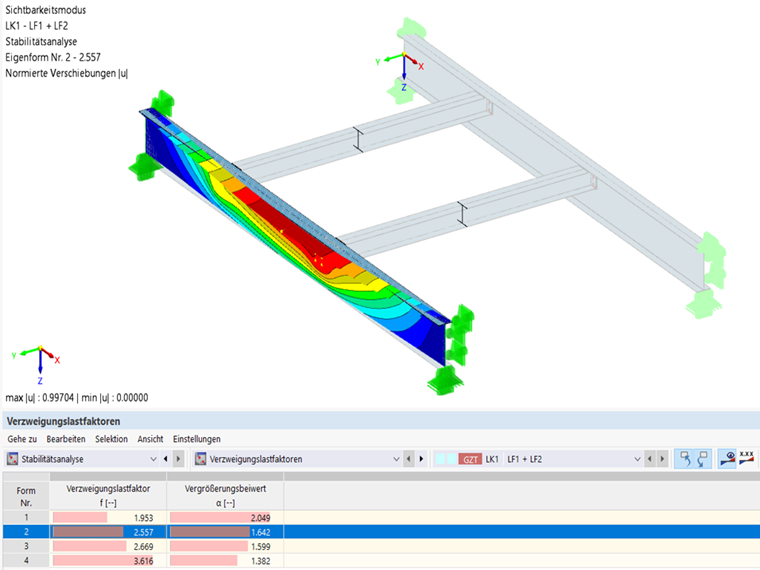
El modelo de análisis por elementos finitos se usa para comprobar si el sistema con 7 grados de libertad en combinación con la estabilidad se calculó correctamente. El modelo por el MEF representa el sistema como antes, por lo que las conexiones de las vigas secundarias también se modelaron como articuladas con chapas en los extremos y las cargas se aplicaron al ala superior de las vigas. Ahora se lleva a cabo un análisis de estabilidad en este sistema estructural. Como resultado, también obtenemos el pandeo torsional del ala superior con un factor de carga crítica de 2,557; es decir, casi la misma que la del sistema con 7 grados de libertad.