Układ konstrukcyjny
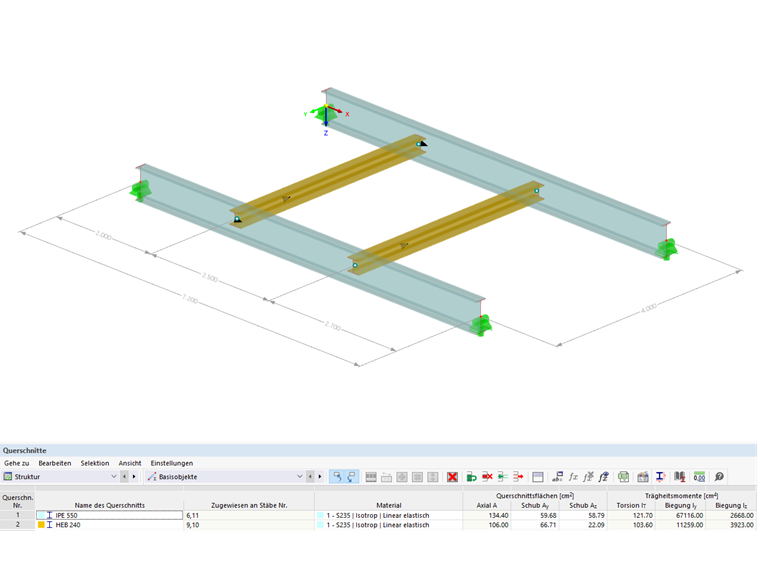
Przekroje :
Belki główne = IPE 550
Belki drugorzędne = HE-B 240
Materiał :
Stal konstrukcyjna S235 zgodnie z DIN EN 1993-1-1, Tabela 3.1
Obciążenia obliczeniowe
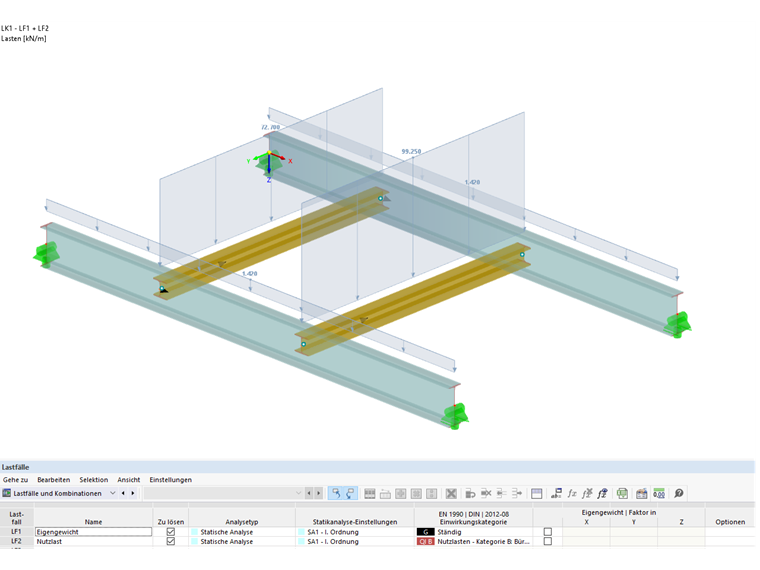
PO 1 Ciężar własny:
gd = 1,42 kN/m
PO 2 Obciążenie użytkowe:
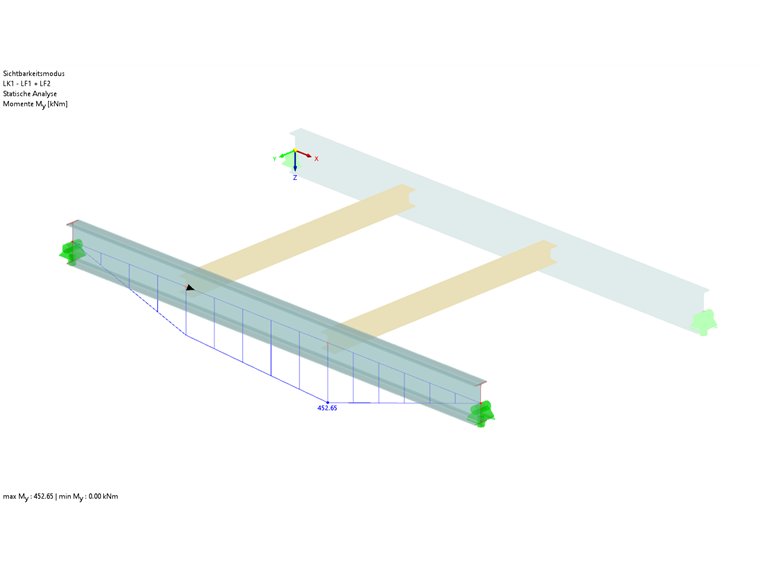
Obliczeniowe siły wewnętrzne
Analiza stateczności bez uwzględnienia belek drugorzędnych zgodnie z EN 1993-1-1 pkt. 6.3.2
Przy założeniu, że pręt jest podparty na początku i na końcu pręta, wyznaczono idealny moment krytyczny dla zwichrzenia Mcr wynoszący 365 kNm. Obliczenia stanu granicznego nośności według równania 6.55 zwracają proporcję wytężenia równą 1.65. Niezbędne jest zastosowanie stabilizacji za pomocą belek drugorzędnych aby spełnić warunki stanów granicznych.
Analiza stateczności z uwzględnieniem belek drugorzędnych zgodnie z EN 1993-1-1, Załącznik BB.2.2
Zasady zawarte w DIN EN 1993-1-1, załącznik BB.2.2 zakładają podporę na całej długości belki, która blokuje możliwość obrotu. Z tego względu dostępne w modelu dyskretne utwierdzenie obrotowe jest „rozmazane“ na ciągłe utwierdzenie obrotowe.
Określenie dostępnego ciągłego utwierdzenia obrotowego:
Wartości zaczerpnięto z [2] i dostosowano jedynie do zapisu załącznika BB.2.2.
Cθ,R,k = 11,823 kNm (część z odkształcenia na zginanie belek drugorzędnych)
Cθ,D,k = 359 kNm (uwzględnione połączenie ze środnikiem)
Przejście na ciągłe utwierdzenie obrotowe Cθ na podstawie belek poprzecznych i średniej odległości między belkami poprzecznymi:
Określenie wymaganego utwierdzenia obrotowego:
gdzie:
Kυ = 0,35 dla stopnia wykorzystania przekroju sprężystego
Kθ = 10 zgodnie z DIN EN 1993-1-1/NA, tabela BB.1
Możliwa jest redukcja Cθ,min o (MEd/Mel,Rd )²:
Wymiarowanie:
Cθ,prov = 134 kNm/m < Cθ,min = 200,9 kNm/m
Nie można przeprowadzić obliczeń w postaci sprawdzenia dostatecznego utwierdzenia bocznego odkształcenia głównej belki zgodnie z załącznikiem BB.2.2.
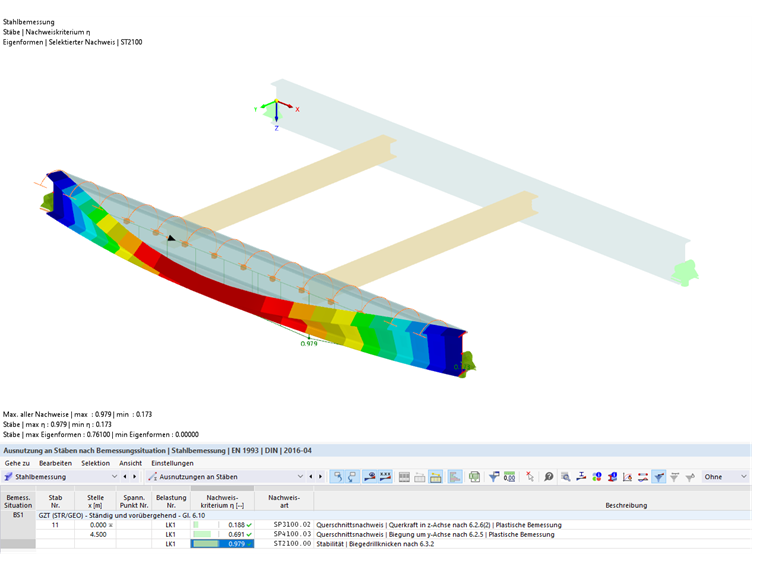
Analiza stateczności z uwzględnieniem belek poprzecznych zgodnie z EN 1993-1-1, rozdz. 6.3.2, z ciągłym utwierdzeniem obrotowym
Ponieważ nie można było zaprojektować wystarczającego stężenia bocznego zgodnie z załącznikiem BB.2.2, istniejące utwierdzenie jest dodatkowo uwzględniane w obliczeniach układu zgodnie z sekcją 6.3.2 w celu sprawdzenia, czy jest ono wystarczające.
Ze względu na zastosowaną sztywność ciągłą skrętną Cθ, prov = 134 kNm/m, sprężysty moment krytyczny wzrasta do Mcr = 982 kNm. Wynika to z pomnożenia przez obliczeniowy moment zginający i współczynnika rozszerzenia αcr , z którym osiągane jest najmniejsze sprężyste obciążenie krytyczne odkształceniami od płaszczyzny konstrukcyjnej. Współczynnik acr przy ciągłym utwierdzeniu obrotowym wynosi 2,169. Zastosowanie utwierdzenia obrotowego ma zatem korzystny wpływ na obliczenia, dzięki czemu obliczenie według równania 6.55 wynosi ostatecznie 0,979.
Analiza stateczności z uwzględnieniem belek poprzecznych zgodnie z EN 1993-1-1, rozdz. 6.3.2, z dyskretnym utwierdzeniem obrotowym
Poniżej przeanalizowane zostanie zastosowanie dyskretnego utwierdzenia obrotowego.
Określenie dostępnego dyskretnego utwierdzenia obrotowego:
Wartości zaczerpnięto z [2] i dostosowano jedynie do zapisu załącznika BB.2.2.
Cθ,R,k = 11,823 kNm (część z odkształcenia na zginanie belek drugorzędnych)
Cθ,D,k = 359 kNm (uwzględnione połączenie ze środnikiem)
W przypadku obliczeń zgodnie z 6.3.2, współczynnik powiększenia αcr = 2,196 określany jest z dyskretnym utwierdzeniem obrotowym. Wynikiem jest moment Mcr 452,65 kNm ∙ 2,196 = 994,09 kNm.
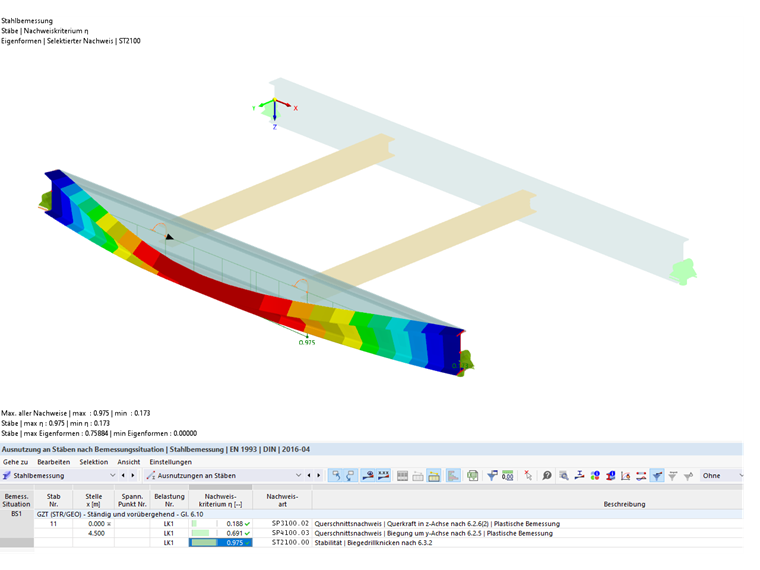
Wynikiem obliczeń według równania 6.55 dla układu jest zatem 0,975.
Analiza stateczności z uwzględnieniem belek poprzecznych według analizy drugiego rzędu z uwzględnieniem skręcania skrępowanego z 7 stopniem swobody.
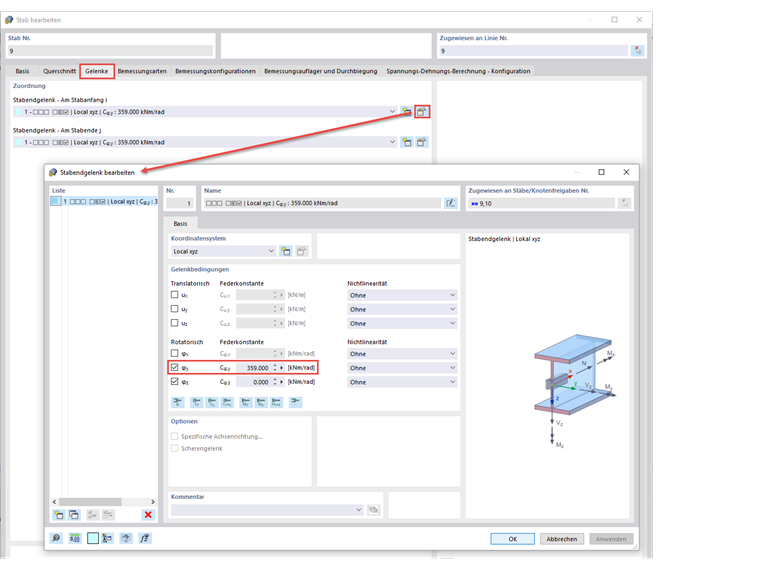
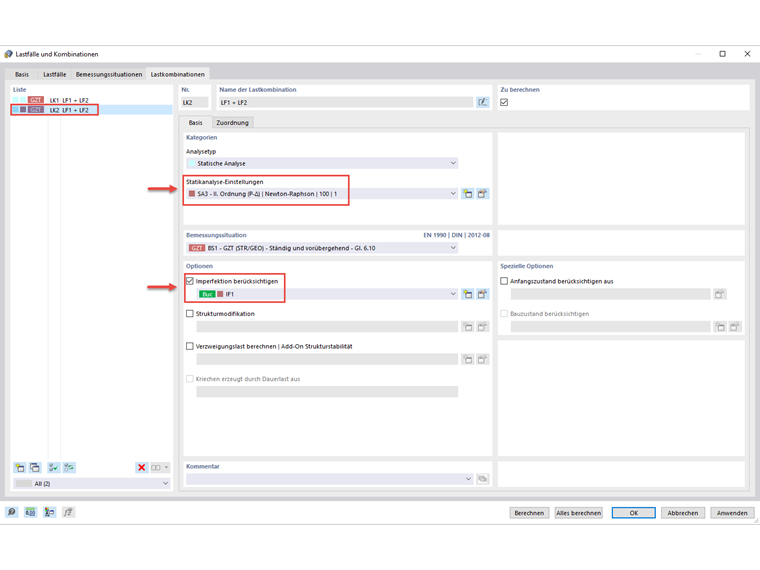
W tym celu w danych ogólnych należy aktywować rozszerzenia „Stateczność konstrukcji” i „Skręcanie skrępowane”. Ponadto, ważne jest, aby wyłączyć analizę stateczności w układach obliczeniowych, ponieważ obliczenia powinny być przeprowadzane w postaci obliczeń przekrojów zgodnie z analizą drugiego rzędu, z uwzględnieniem imperfekcji i zastosowania γm1. Następnie modyfikowane są przeguby na końcach prętów belek poprzecznych.
Przy określaniu istniejącego dyskretnego utwierdzenia obrotowego pomijana jest składowa odkształcenia belek poprzecznych C, R, k , ponieważ interakcja belek głównych i poprzecznych jest już uwzględniona w modelu z 7 stopniami swobody. Zatem konieczne jest uwzględnienie sprężystości wynikającej z odkształcenia przekroju belki głównej przy Cθ, D, k = 359 kNm. Ta stała sprężystości jest używana do modyfikowania przegubów na końcach prętów belek drugorzędnych. Ponadto należy upewnić się, że wszystkie działające obciążenia są przyłożone na górnej krawędzi przekroju lub w niekorzystnym, mimośrodowym położeniu.
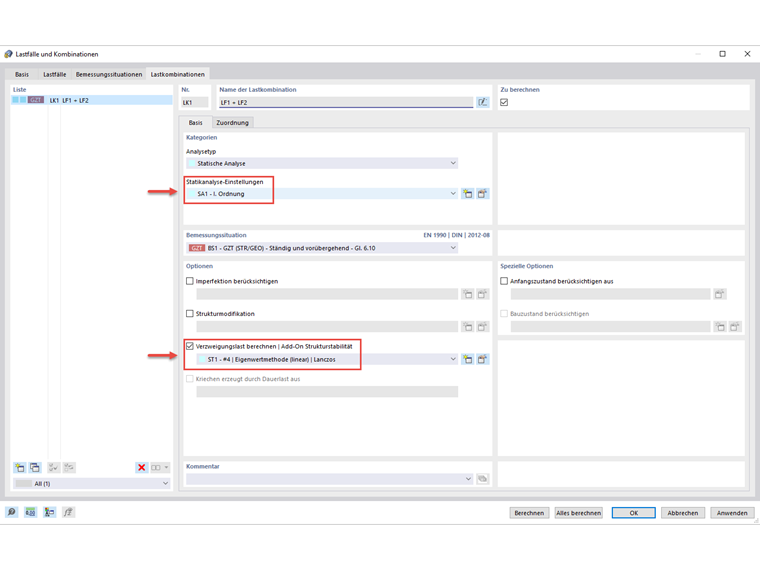
Ponieważ obliczenia są przeprowadzane zgodnie z analizą drugiego rzędu, imperfekcje również muszą zostać uwzględnione. Odbywa się to poprzez określenie postaci wyboczenia lub skrętnej przy użyciu rozszerzenia „Stateczność konstrukcji”. W tym celu należy zastosować kombinację obciążeń (tutaj: KO1) oblicza obciążenie krytyczne zgodnie z liniową analizą statyczną, a następnie generuje imperfekcję na podstawie wynikowego wektora własnego.
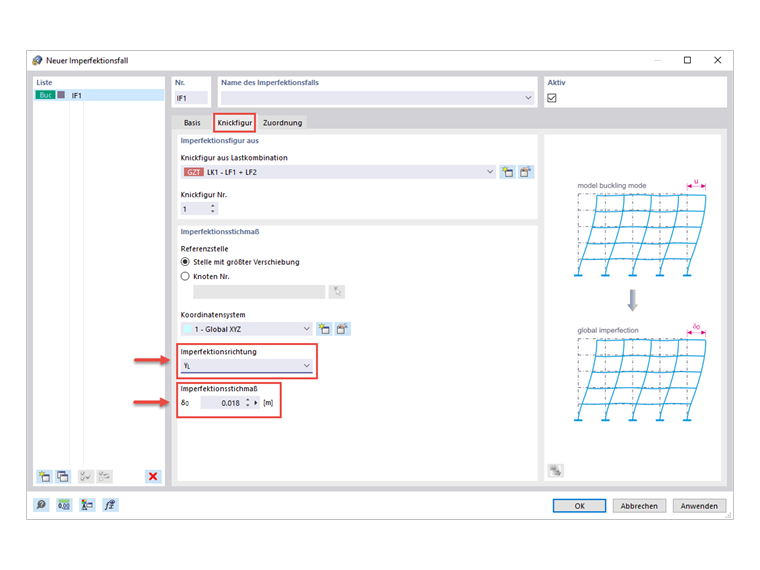
Aby utworzyć tę imperfekcję, należy najpierw utworzyć nowy przypadek imperfekcji, oparty na postaci wyboczeniowej od kombinacji obciążeń. W tym miejscu należy między innymi określić skok imperfekcji, który wynika z iloczynu wykorzystania przekroju e0/L i długości L przekroju. Stopień wykorzystania przekroju zależy od rodzaju przekroju i jego wymiarów. Ponieważ główne belki modelu składają się z walcowanych dwuteowników o wymiarach h/b > 2, przyjmuje się stosunek przekrojów e0/L = 1/400. Przy długości przekroju L = 7,20 m wymiar imperfekcji wynosi ostatecznie 0,018 m w kierunku y.
Ten przypadek imperfekcji należy teraz przypisać do kombinacji obciążeń. Aby uniknąć odniesienia cyklicznego, tworzona jest nowa kombinacja obciążeń poprzez skopiowanie PO, na którym oparta jest imperfekcja, i obliczenie jej zgodnie z analizą drugiego rzędu.
Podczas wymiarowania konstrukcji stalowej przeprowadzane jest teraz wymiarowanie przekroju według analizy drugiego rzędu, z uwzględnieniem imperfekcji. Na podstawie wyznaczonych sił wewnętrznych uzyskuje się ostatecznie stopień wykorzystania 0,987 według równania 6.1.
Sprawdzenie poprawności obliczeń z wykorzystaniem modelu MES
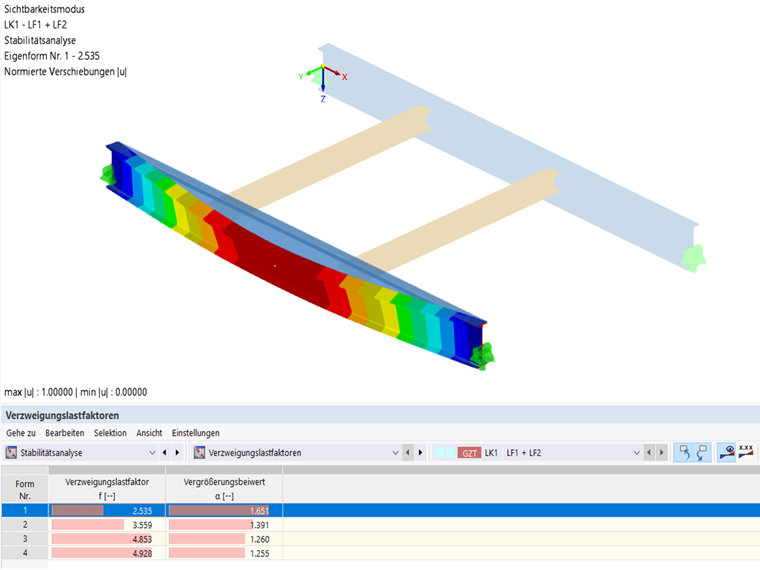
Podczas analizy stateczności KO 1 na modelu o 7 stopniach swobody zastosowano współczynnik obciążenia krytycznego 2.535, co zostanie sprawdzone poniżej przy użyciu modelu MES.
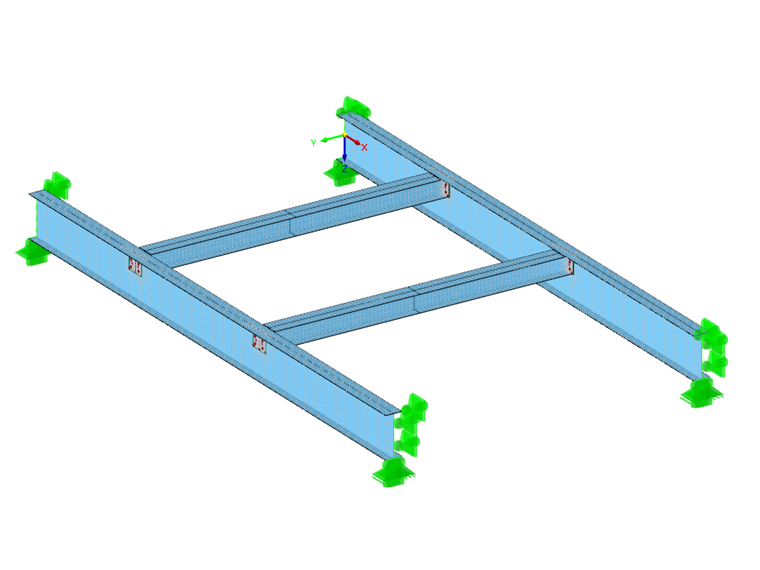
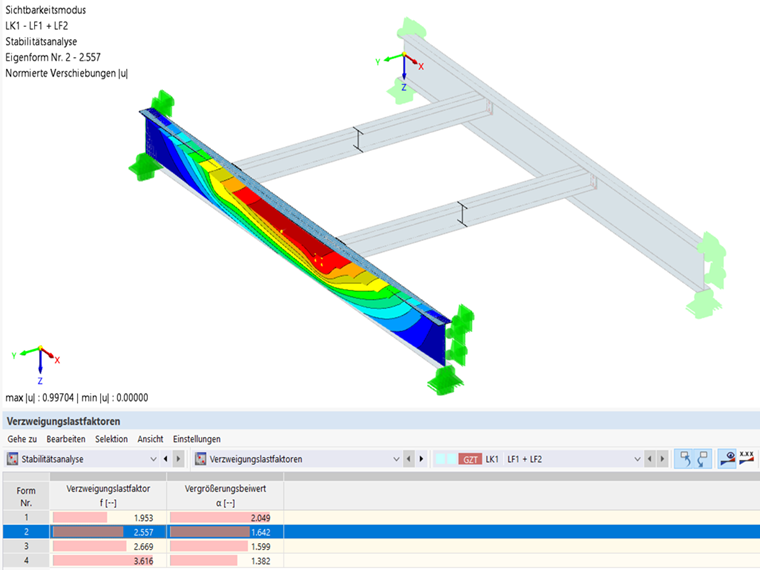
Model MES służy do sprawdzenia, czy układ został poprawnie obliczony z uwzględnieniem 7 stopni swobody w połączeniu ze statecznością. Model MES reprezentuje układ jak poprzednio; również w tym przypadku połączenia belek poprzecznych zostały zamodelowane jako połączenia przegubowe z blachami czołowymi, a obciążenia zostały przyłożone do górnej półki belki. Układ ten pokazuje teraz analizę stateczności. Wynikiem jest również wyboczenie skrętne górnego pasa ze współczynnikiem obciążenia krytycznego 2.557, czyli prawie identycznym jak dla układu o 7 stopniach swobody.