7510x

001433

Dipl.-Ing. (BA) Markus Baumgärtel

03.05.2017

Modèle de sol avec dépassement de fondation

Un article précédent vous présentait les différentes variantes de fondations de sol élastiques, ainsi que la méthode de calcul de modules de sols. Cet article-ci décrit une autre méthode pour les fondations de surface. Cette méthode considère les zones de sol adjacentes par un dépassement des fondations. Dans ce cas, les paramètres de fondation sont considérés selon les travaux de Pasternak et Barwaschow.

Équation selon Pasternak

\begin{array}{l} c_{1} = \frac{E_{0}}{H \cdot (1 - 2 \cdot μ ²)} \\ c_{2} = E_{0} \cdot \frac{H}{6 \cdot (1 μ)} \end{array}

Formule 1

où

E_{s} \cdot \frac{1 - μ - 2 \cdot μ ²}{1 - μ}

Formule 4

H = épaisseur de la fondation
μ = coefficient de Poisson

Équation selon Barwaschow

\begin{array}{l} c_{1} = \frac{E_{0}}{H \cdot (1 - μ ²)} \\ c_{2} = E_{0} \cdot \frac{H}{20 \cdot (1 - μ ²)} \end{array}

Formule 2

où

E_{0} = E_{s} \cdot \frac{1 - μ - 2 \cdot μ ²}{1 - μ}

Formule 5

H = épaisseur de la fondation

μ = coefficient de Poisson

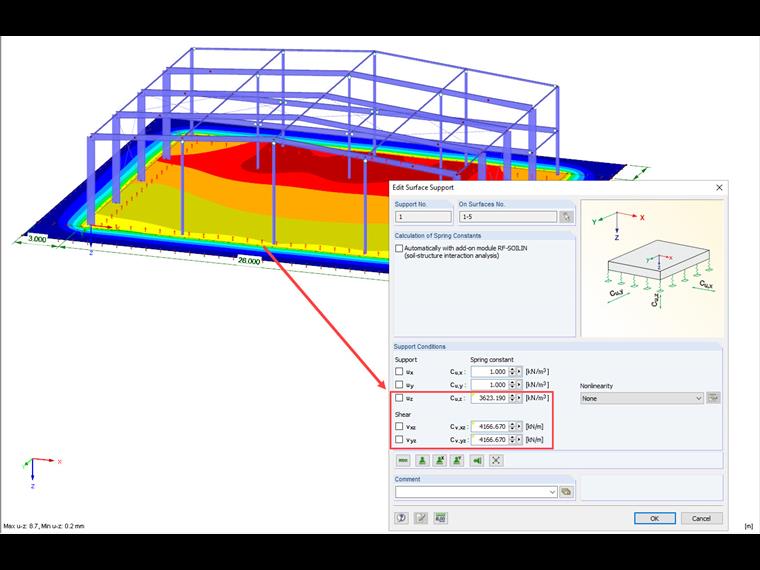
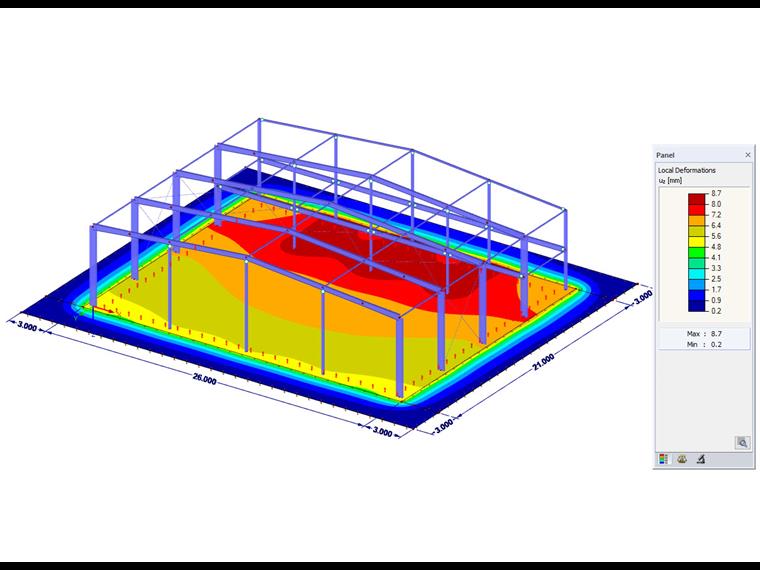
Les recouvrements de fondation appliqués avec cette méthode doivent idéalement atteindre jusqu'à ce que le tassement sur le bord du recouvrement de fondation soit proche de zéro. De plus, l'aire supplémentaire ne doit pas avoir de rigidité déterminante supplémentaire, c'est pourquoi l'épaisseur de recouvrement de fondation doit être maintenue très faible.

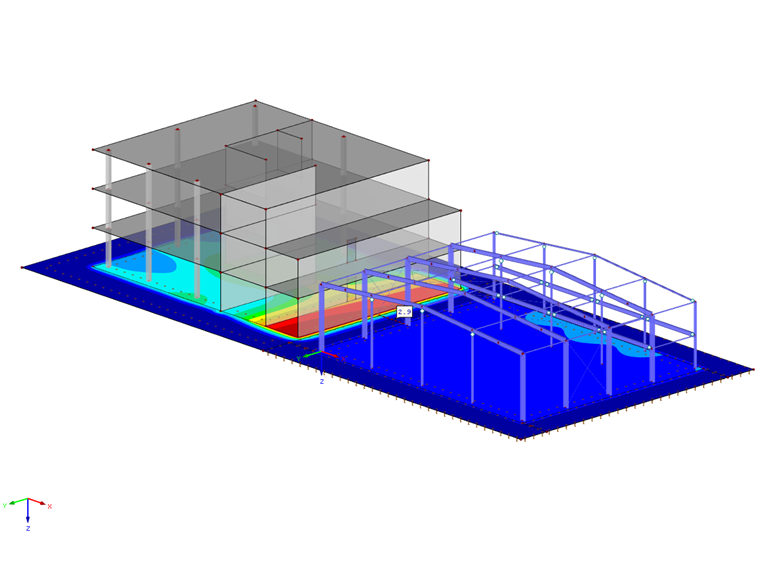
Outre le temps de calcul court, cette variante présente l'avantage de tenir compte de la résistance au cisaillement. De plus, cette méthode vous permet d'afficher graphiquement le comportement du tassement à l'extérieur du bord de la fondation. De cette manière, il est également possible de représenter l'interaction entre plusieurs bâtiments distincts qui s'influencent mutuellement via le bassin de subsidence.

Exemple

E₀ = 10 000 kN/m²
μ = 0,2
H = 3 m

\begin{array}{l} c_{1, z} = \frac{E_{0}}{H \cdot (1 - 2 \cdot μ ²)} = \frac{10.000}{3 \cdot (1 - 2 \cdot 0, 2 ²)} = 3 623, 19 kN / m ² \\ c_{2, v} = E_{0} \cdot \frac{H}{6 \cdot (1 μ)} = 10.000 \cdot \frac{3}{6 \cdot (1 0, 2)} = 4 166, 67 kN / m ² \end{array}

Formule 3

Image 01 - Conditions d'appui pour les fondations de surface

Image 02 - Déformations locales de la dalle de plancher et du col de fondation

Image 03 - Interaction de deux bâtiments séparés

Références

[1] Barth, C.; Rustler, W. : Finite Elemente in der Baustatik-Praxis, 2. édition. Berlin : Beuth, 2013 [2] Kolar, V. ; Nemec, je .: Modelling of Soil-Structure Interaction. Amsterdam : Elsevier Science Publishers, 1989

Base de connaissance

Ko 001433 | Modèle de sol avec dépassement de fondation

Auteur

M. Baumgärtel fournit un support technique aux clients de Dlubal Software.

Liens

Téléchargements

Fichier du modèle RFEM 1

604 KB

Fichier du modèle RFEM 2

47,86 MB

;