Уравнение по Пастернаку
где
H = толщина фундамента
μ = коэффициент Пуассона
Уравнение по Барвашову
где
H = толщина фундамента
μ = коэффициент Пуассона
Нахлесты фундамента, применяемые при этом методе, в идеале должны достигать момента, когда осадка на краю перекрытия фундамента будет близка к нулю. Кроме того, дополнительная площадь не должна иметь никакой дополнительной определяющей жесткости, поэтому толщину перекрытия фундамента следует поддерживать очень низкой.
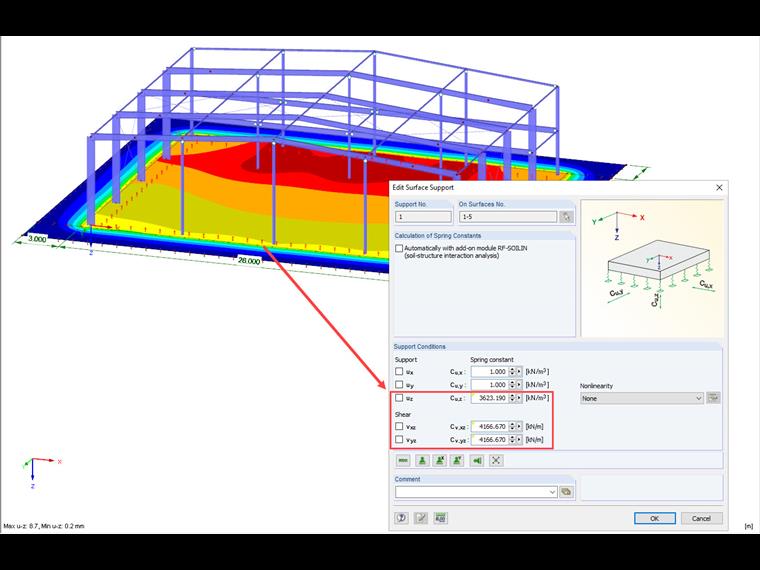
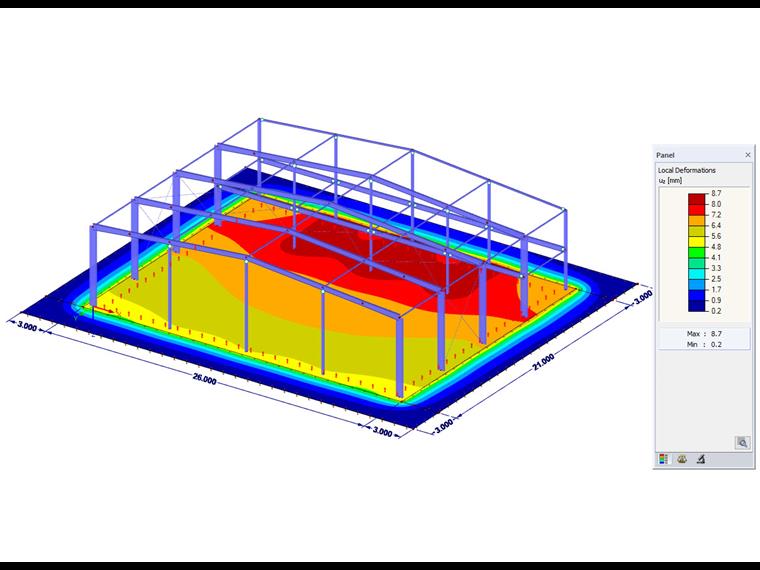
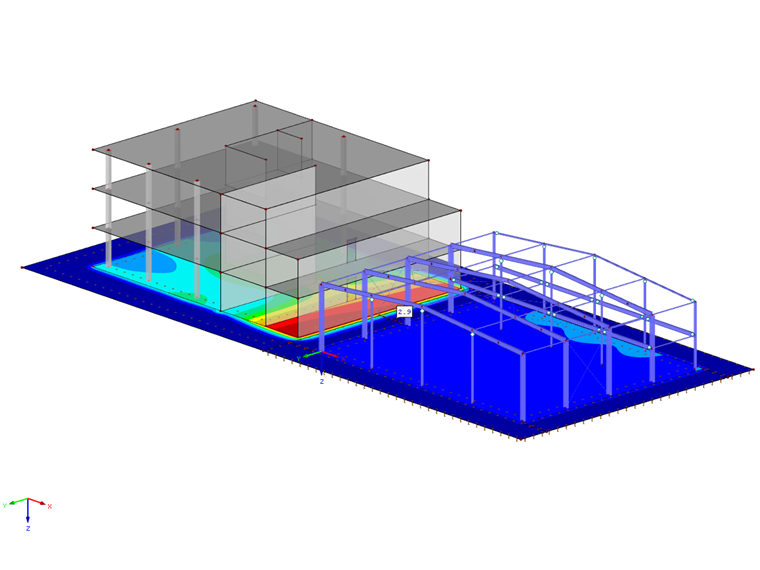
Помимо короткого времени расчета, преимуществом этого варианта является учет сопротивления сдвигу. Кроме того, этот метод позволяет графически отобразить характер осадки за пределами края фундамента. Таким образом, можно также представить взаимодействие нескольких отдельных зданий, которые влияют друг на друга через бассейн осадки.
Пример
E0 = 10 000 кН/м2
μ = 0,2
H = 3 м
Ссылки
[1] Barth, C .; Рустлер, В .: Finite Elemente in der Baustatik-Praxis, 2-й издание. Берлин: Beuth, 2013 [2] Kolar, V .; Nemec, I .: Моделирование взаимодействия грунт-конструкция. Амстердам: Издательство Elsevier Science, 1989 г.
.png?mw=350&hash=08a561dc3d1b94edf5b16c9962561142b7b844d3)
