7363x

001433

Dipl.-Ing. (BA) Markus Baumgärtel

3.5.2017

Model spolupůsobícího podloží

V našem dřívějším příspěvku jsme se zabývali různými možnostmi posouzení podloží ploch vedle klasické metody pružinových konstant. V následujícím příspěvku představíme další metodu posouzení uložení ploch. Tato metoda zohledňuje i přilehlou oblast podloží mimo vlastní základ zadáním přesahu, jakéhosi „límce“. Parametry podloží přitom přebíráme z obsáhlejších prací Pasternaka a Barvačova.

Rovnice podle Pasternaka

\begin{array}{l} c_{1} = \frac{E_{0}}{H \cdot (1 - 2 \cdot μ ²)} \\ c_{2} = E_{0} \cdot \frac{H}{6 \cdot (1 μ)} \end{array}

Vzorec 1

kde

{m a t h r m E}_{} m a t h r m s \cdot f r a c d i s p l a y s t y l e 1 - m a t h r m m u - 2 \cdot m a t h r m m u ² 1 - m a t h r m m u

Vzorec 4

H = tloušťka podloží
μ = Poissonův součinitel

Rovnice podle Barvačova

\begin{array}{l} c_{1} = \frac{E_{0}}{H \cdot (1 - μ ²)} \\ c_{2} = E_{0} \cdot \frac{H}{20 \cdot (1 - μ ²)} \end{array}

Vzorec 2

kde

E_{0} = E_{s} \cdot \frac{1 - μ - 2 \cdot μ ²}{1 - μ}

Vzorec 5

H = tloušťka podloží

μ = Poissonův součinitel

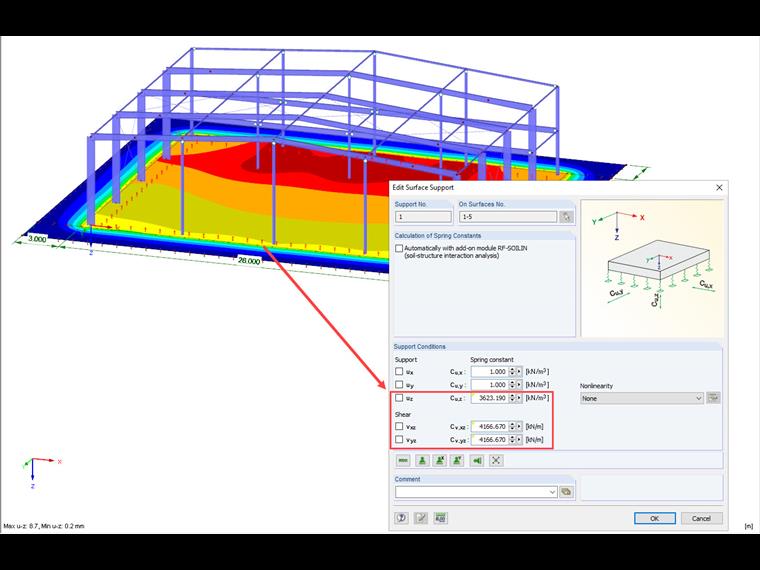
„Límec“ spolupůsobícího podloží by se při tomto postupu měl ideálně uvažovat do takové vzdálenosti, aby se sedání na okraji „límce“ blížilo nule. Tato přídavná oblast by dále neměla mít žádnou rozhodující přídavnou tuhost, a proto by se měla uvažovat u tohoto „límce“ velmi malá tloušťka.

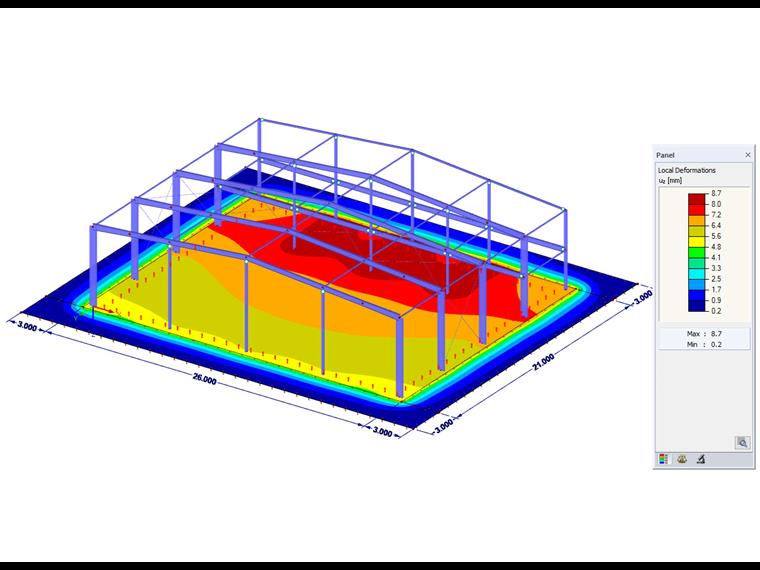
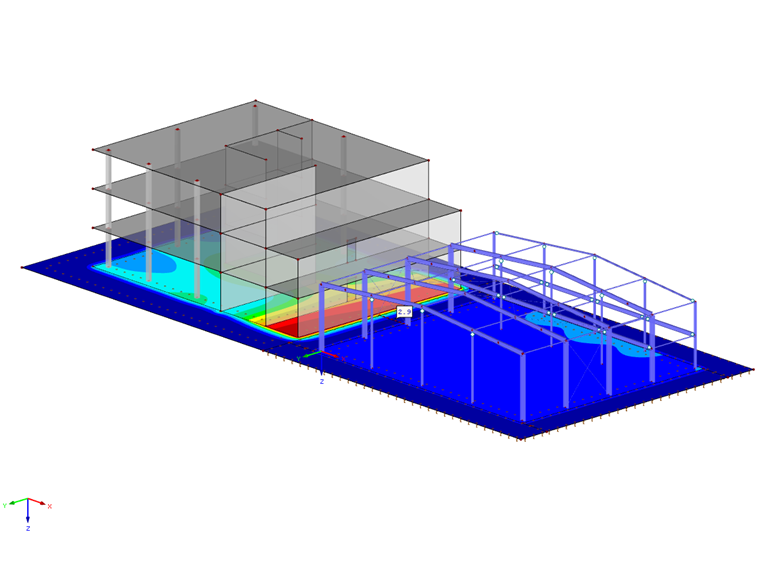
Výhodou dané metody je kromě krátké doby trvání výpočtu také zohlednění únosnosti ve smyku. Navíc tato metoda umožňuje znázornit graficky průběh sedání vně hrany základu. Lze tak vysledovat také interakci několika nezávislých konstrukcí, které se vzájemně ovlivňují přes poklesovou kotlinu.

Příklad použití

E₀ = 10 000 kN/m²
μ = 0,2
H = 3 m

\begin{array}{l} c_{1, z} = \frac{E_{0}}{H \cdot (1 - 2 \cdot μ ²)} = \frac{10.000}{3 \cdot (1 - 2 \cdot 0, 2 ²)} = 3 623, 19 kN / m ² \\ c_{2, v} = E_{0} \cdot \frac{H}{6 \cdot (1 μ)} = 10.000 \cdot \frac{3}{6 \cdot (1 0, 2)} = 4 166, 67 kN / m ² \end{array}

Vzorec 3

Obrázek 01 - Podmínky podpory plošného podloží

Obrázek 02 - Lokální deformace stropní desky a základového límce

Obrázek 03 - Interakce dvou samostatných budov

Reference

[1] Barth, C .; Rustler, W .: Finite Elemente in der Baustatik-Praxis, 2. vydání. Berlín: Beuth, 2013 [2] Kolář, V .; Němec, I.: Modelling of Soil-Structure Interaction. Amsterdam: Elsevier Science Publishers, 1989

Databáze znalostí

KB 001433 | Model spolupůsobícího podloží

Autor

Ing. Baumgärtel zajišťuje technickou podporu zákazníkům společnosti Dlubal Software.

Odkazy

Stahování

Model 1 v programu RFEM

604 KB

Model 2 v programu RFEM

47,86 MB

;