8297x

001493

21.11.2017

Vérification des soudures d’angle aux âmes des poutres support de chemins de roulement selon EN 1993-6

Pour conclure sur le sujet de la vérification des soudures sur les chemins de roulement, après les articles techniques sur le cordon de soudure du rail à l’état limite ultime et à l’état limite de fatigue, voici un article technique sur les soudures d'angle de l'âme. L’état limite ultime et l’état limite de fatigue sont considérés.

État limite ultime

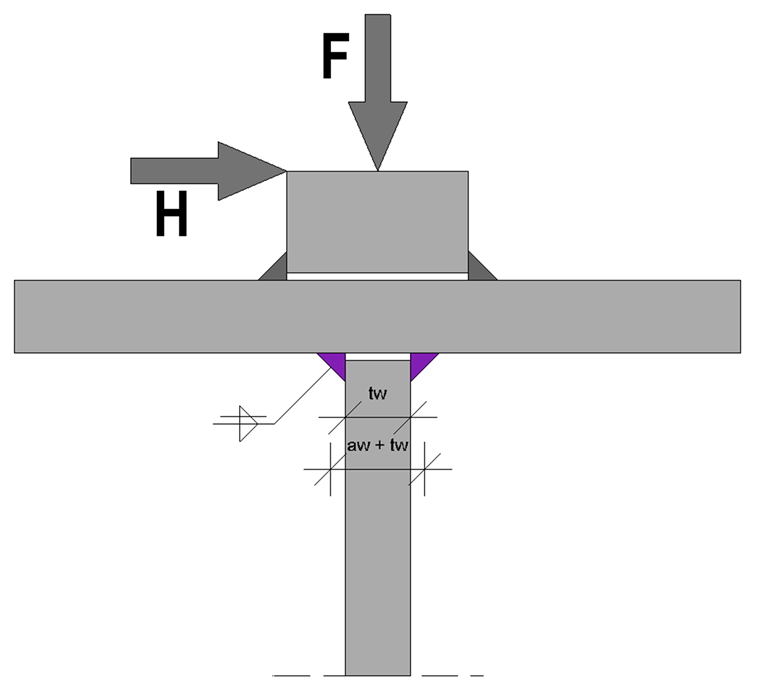
Les charges appliquées entraînent des charges de galets horizontales et verticales qui doivent être considérées dans le calcul. L’application d’une charge de galet excentrée des charges de galet verticales n’est pas considérée dans le calcul à l’état limite ultime et aucun moment de torsion supplémentaire n’apparaît donc.

Soudures d’âme comme doubles soudures d’angle

Voici un ensemble de formules pour le calcul des contraintes.

Contraintes dues à la charge de galet

\begin{array}{l} \max σ_{⊥} = \frac{F_{z, Ed} H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} \max τ_{⊥} = \frac{F_{z, Ed} H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} \\ τ_{⊥} = \frac{F_{z, Ed} - H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} σ_{⊥} = \frac{F_{z, Ed} - H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} \\ τ_{∥} = \frac{V_{Ed} \cdot S_{y}}{l_{y} \cdot 2 \cdot a_{w}} τ_{∥} = \frac{V_{Ed} \cdot S_{y}}{l_{y} \cdot 2 \cdot a_{w}} \\ σ_{v, w, Ed} = \sqrt{σ_{⊥} ² 3 \cdot τ_{⊥} ² 3 \cdot τ_{∥} ²} σ_{v, w, Ed} = \sqrt{σ_{⊥} ² 3 \cdot τ_{⊥} ² 3 \cdot τ_{∥} ²} \end{array}

Formule 1

Vérification de la soudure

\begin{array}{l} σ_{v, w, Rd} = \frac{f_{u}}{β_{w} \cdot γ_{M 2}} \frac{σ_{v, w, Ed}}{σ_{v, w, Rd}} \leq 1, 00 \\ σ_{⊥, w, Rd} = \frac{0, 9 \cdot f_{u}}{γ_{M 2}} \frac{σ_{⊥, w, Ed}}{σ_{⊥, w, Rd}} \leq 1, 00 \end{array}

Formule 2

État limite de fatigue

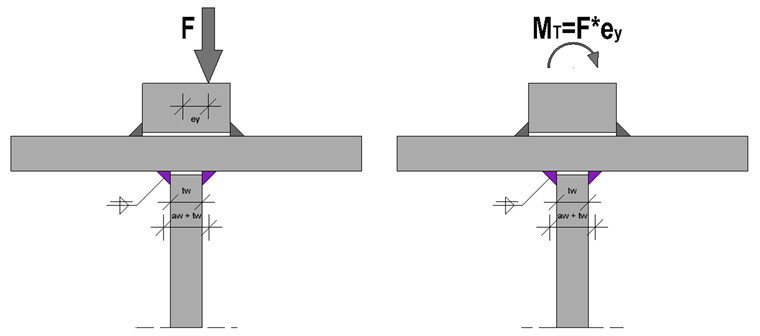
Contrairement à l’ELU, les contraintes résultant des charges horizontales sont négligées, ainsi, seules les charges verticales des roues sont prises en compte. Cependant, en fonction de la classe d’endommagement existante et de l’Annexe Nationale utilisée, une charge excentrée de galets de 1/4 de la largeur du champignon du rail doit être considérée. Il en résulte un moment de torsion supplémentaire qui doit d’abord être transféré par les soudures de rail, puis par la semelle supérieure, l’âme et enfin par les soudures d’âme.

Application de charges de galet excentrées à l’état limite de fatigue

Les soudures de rail doivent transférer ce moment de torsion presque entièrement. D’autre part, l’effet de la rigidité en torsion de la semelle supérieure doit être considéré pour les soudures sur l’âme car cela a une influence cruciale sur la flexion de l’âme et donc sur la contrainte dans la soudure.

Lors de la détermination de la constante de torsion de la semelle supérieure, [2] ne considère que la semelle supérieure tant que le rail n’est pas fixé de manière rigide. Ce n’est que dans ce cas que le moment de torsion est déterminé à partir du rail et de la semelle. Une autre approche est décrite dans [5], où les composants individuels de rigidité en torsion du rail et de la semelle sont additionnés de sorte qu’il est possible d’obtenir une rigidité plus élevée de la semelle supérieure. Cependant, cette approche n’est pas fournie dans [2].

Deux composantes de contrainte doivent être combinées pour le calcul des soudures d’angle de l’âme. Il y a les contraintes dues à la charge de galet centrée et les contraintes dues au moment de torsion. Le moment de torsion total M_T est partiellement absorbé par la semelle supérieure, ainsi, l’âme du composant M_âme due à la flexion de l’âme reste pour la vérification de la soudure.

Enfin, il convient de noter que cette procédure de calcul et cette description ne s’appliquent qu’aux doubles soudures d'angle entre la semelle supérieure et l’âme. Si les soudures de la semelle inférieure et de l’âme doivent également être calculées comme des soudures d’angle, les effets des charges de galets sont négligeables en raison de la longueur existante des charges de galets appliquées. Dans ce cas, les composantes des contraintes de flexion ou de cisaillement ainsi que les épaisseurs minimales sont déterminantes.

Vous trouverez ci-dessous un ensemble de formules pour le calcul des contraintes et de vérification.

Contraintes dues à la charge de galet centrée

σ_{z, Ed, cen, WELD} = \frac{F_{z, Ed}}{2 \cdot a_{w} \cdot l_{eff}}

Formule 3

Contraintes dues à la charge de galet excentrée

\begin{array}{l} M_{T} = F_{z, Ed} \cdot \frac{b_{Rail}}{4} \\ β = \frac{π \cdot h_{w}}{a} \\ I_{T, chord} = \frac{b_{cs} \cdot t_{f} ³}{3} \\ λ = \sqrt{\frac{2, 98 \cdot t_{w} ³}{a \cdot I_{T}} \cdot \frac{\sin h ² (β)}{\sin h (2 \cdot β) - 2 \cdot β}} \\ σ_{z, Ed, ecc} = \frac{6}{t_{w} ²} \cdot M_{T} \cdot \frac{λ}{2} \cdot \tan h (\frac{λ \cdot a}{2}) \\ M_{web} = σ_{z, Ed, ecc} \cdot \frac{t_{w} ² \cdot l_{eff}}{6} \\ σ_{z, Ed, ecc, WELD} = \frac{M_{web}}{(t_{w} a_{w}) \cdot a_{w} \cdot l_{eff}} \end{array}

Formule 4

Contrainte résultante dans la soudure

σ_{z, Ed} = σ_{z, Ed, cen, WELD} σ_{z, Ed, ecc, WELD}

Formule 5

Vérifications

\begin{array}{l} \frac{γ_{Ff} \cdot ∆ σ_{E, 2}}{\frac{∆ σ_{c}}{γ_{Mf}}} < 1, 00 \\ \frac{γ_{Ff} \cdot ∆ τ_{E, 2}}{\frac{∆ τ_{c}}{γ_{Mf}}} < 1, 00 \end{array}

Formule 6

Conclusion

Les trois articles techniques consacrés aux différentes soudures des poutres de pont roulant détaillent ce sujet. Lors de la mise en œuvre pratique dans des cas individuels, il convient en particulier de décider si la rigidité en torsion de la semelle supérieure en tant qu’addition des composants individuels du rail et de la semelle ou de la semelle seule doit être appliquée.

Liens

Logiciels pour le calcul statique et l'analyse de grues et ponts roulants

Références

Seeßelberg, C. Kranbahnen: Bemessung und konstruktive Gestaltung nach Eurocode, 5. édition. Berlin : Bauwerk, 2016
Eurocode 3 : calcul des structures en acier - Partie 6 : Kranbahnen; EN 1993-6:2007 + AC:2009
Comité Européen de normalisation (CEN). (2010) Eurocode 1 : Einwirkungen auf Tragwerke - Teil 3: Einwirkungen infolge von Kranen und Maschinen; DIN EN 1991-3:2010-12
Eurocode 3 : calcul des structures en acier - Partie 1‑9: Ermüdung; EN 1993-1-9:2005 + AC:2009
Petersen, C.: Stahlbau, 4e édition. Wiesbaden : Springer Vieweg, 2013

Chemin de roulement Soudures d’angle de l’âme Cordon de soudure

;