7428x

001493

2017-11-21

Design of Web Fillet Welds of Crane Girders According to EN 1993-6

At the end of the topic on the design of welds on runway beams - after the technical articles about the rail weld seam in the ultimate limit state and the limit state of fatigue - a technical article about web fillet welds now follows. Both the ultimate limit state and the fatigue limit state are considered.

Ultimate limit state

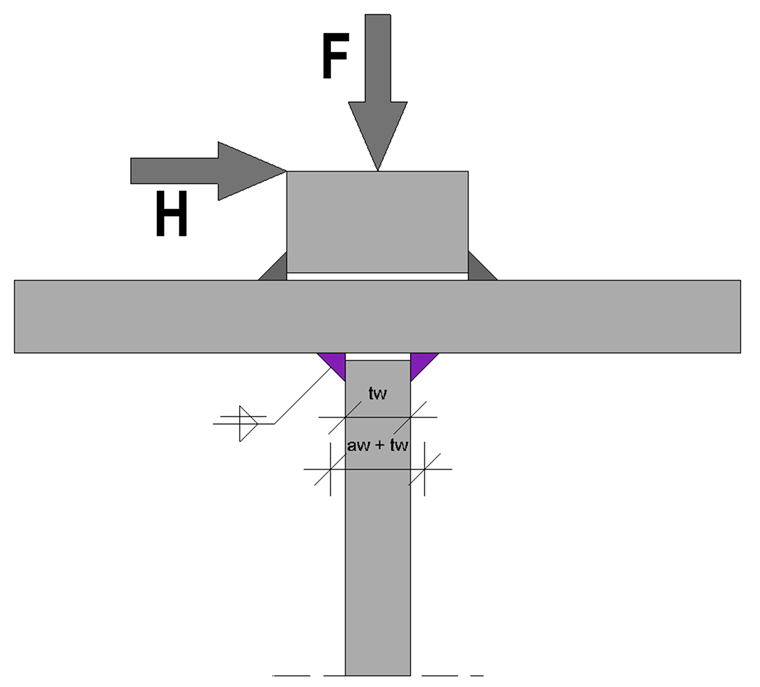
The applied loads cause both horizontal and vertical wheel loads that must be considered in the design. An eccentric wheel load application of the vertical wheel loads is not considered in the ultimate limit state design, and therefore no additional torsional moment occurs.

Web Welds as Double Fillet Welds

In the following text is a set of formulas for the stress and design calculation.

Stresses Due to Wheel Load

\begin{array}{l} \max σ_{⊥} = \frac{F_{z, Ed} H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} \max τ_{⊥} = \frac{F_{z, Ed} H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} \\ τ_{⊥} = \frac{F_{z, Ed} - H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} σ_{⊥} = \frac{F_{z, Ed} - H_{Ed}}{2 \cdot \sqrt{2} \cdot a_{w} \cdot l_{eff}} \\ τ_{∥} = \frac{V_{Ed} \cdot S_{y}}{l_{y} \cdot 2 \cdot a_{w}} τ_{∥} = \frac{V_{Ed} \cdot S_{y}}{l_{y} \cdot 2 \cdot a_{w}} \\ σ_{v, w, Ed} = \sqrt{σ_{⊥} ² 3 \cdot τ_{⊥} ² 3 \cdot τ_{∥} ²} σ_{v, w, Ed} = \sqrt{σ_{⊥} ² 3 \cdot τ_{⊥} ² 3 \cdot τ_{∥} ²} \end{array}

Formula 1

Weld Design

\begin{array}{l} σ_{v, w, Rd} = \frac{f_{u}}{β_{w} \cdot γ_{M 2}} \frac{σ_{v, w, Ed}}{σ_{v, w, Rd}} \leq 1.00 \\ σ_{⊥, w, Rd} = \frac{0.9 \cdot f_{u}}{γ_{M 2}} \frac{σ_{⊥, w, Ed}}{σ_{⊥, w, Rd}} \leq 1.00 \end{array}

Formula 2

Fatigue limit state

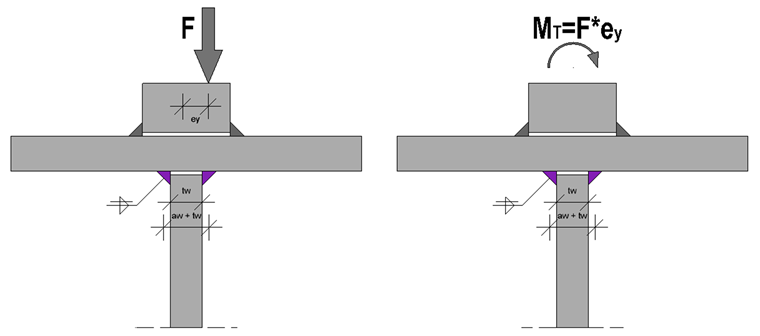
In contrast to the ULS, the stresses resulting from horizontal loads are neglected; thus, only the vertical wheel loads are taken into account. However, depending on the existing damage class and the National Annex used, the eccentric wheel load of 1/4 of the rail head width must be considered. Thus, an additional torsional moment occurs, which must be transferred by the rail welds first, and then by the top flange, the web and finally by the web welds.

Eccentric Wheel Load Application in GZE

The rail welds must transfer this torsional moment almost entirely. On the other hand, the effect of the torsional stiffness of the top flange should be considered for the welds on the web as this has a crucial influence on the web bending and thus on the stress in the weld.

When determining the torsional constant of the top flange, [2] only assumes the top flange as long as the rail is not rigidly fixed. Only in that case is the torsional moment determined from the rail and the flange. Another approach is described in [5], where the individual torsional stiffness components of the rail and the flange are added together so it is possible to achieve higher stiffness of the top flange. However, this approach is not provided in [2].

It is necessary to combine two stress components for the design of the web fillet welds. There are the stresses due to the centric wheel load and the stresses due to the torsional moment. The full torsional moment M_T is partially absorbed by the top flange; thus, the component M_web due to the web bending remains for the weld design.

Finally, it should be noted that this calculation procedure and description only applies to the double fillet welds between the top flange and the web. If the welds on the bottom flange and the web should also be designed as fillet welds, the wheel load effects are negligibly small due to the existing length of the applied wheel loads. In this case, the stress components due to bending or shear stress as well as the minimum thicknesses are governing.

In the following text is a set of formulas for the stress and design calculation.

Stresses Due to Centric Wheel Load

σ_{z, Ed, cen, weld} = \frac{F_{z, Ed}}{2 \cdot a_{w} \cdot l_{eff}}

Formula 3

Stresses Due to Eccentric Wheel Load

\begin{array}{l} M_{T} = F_{z, Ed} \cdot \frac{b_{rail}}{4} \\ β = \frac{π \cdot h_{w}}{a} \\ I_{T, chord} = \frac{b_{cs} \cdot t_{f} ³}{3} \\ λ = \sqrt{\frac{2.98 \cdot t_{w} ³}{a \cdot I_{T}} \cdot \frac{\sin h ² (β)}{\sin h (2 \cdot β) - 2 \cdot β}} \\ σ_{z, Ed, ecc} = \frac{6}{t_{w} ²} \cdot M_{T} \cdot \frac{λ}{2} \cdot \tan h (\frac{λ \cdot a}{2}) \\ M_{web} = σ_{z, Ed, ecc} \cdot \frac{t_{w} ² \cdot l_{eff}}{6} \\ σ_{z, Ed, ecc, weld} = \frac{M_{web}}{(t_{w} a_{w}) \cdot a_{w} \cdot l_{eff}} \end{array}

Formula 4

Resulting Stress in Weld

σ_{z, Ed} = σ_{z, Ed, cen, weld} σ_{z, Ed, ecc, weld}

Formula 5

Designs

\begin{array}{l} \frac{γ_{Ff} \cdot ∆ σ_{E, 2}}{\frac{∆ σ_{c}}{γ_{Mf}}} < 1.00 \\ \frac{γ_{Ff} \cdot ∆ τ_{E, 2}}{\frac{∆ τ_{c}}{γ_{Mf}}} < 1.00 \end{array}

Formula 6

Summary

The three technical articles about various welds of crane girders explain this topic in detail. In the practical implementation in individual cases, it should be decided in particular whether to apply the torsional stiffness of the top flange as an addition of the individual components of the rail and the flange, or the flange only.

Links

Structural Analysis and Design Software for Cranes and Craneways

References

Seeßelberg, C. Kranbahnen: Bemessung und konstruktive Gestaltung nach Eurocode, 5th ed.). Berlin, Bauwerk, 2016
EC 3. (2009). Eurocode 3: Design of Steel Structures - Part 6: Crane Supporting Structures; EN 1993-6:2007 + AC:2009
Eurocode 1: Einwirkungen auf Tragwerke - Teil 3: Einwirkungen infolge von Kranen und Maschinen; DIN EN 1991-3:2010-12
EC 3. (2009). Eurocode 3: Design of Steel Structures - Part 1‑9: Fatigue; EN 1993‑1‑9:2005 + AC:2009
Petersen, C.: Stahlbau, 4. Auflage. Wiesbaden: Springer Vieweg, 2013

;