Mezní stav únosnosti
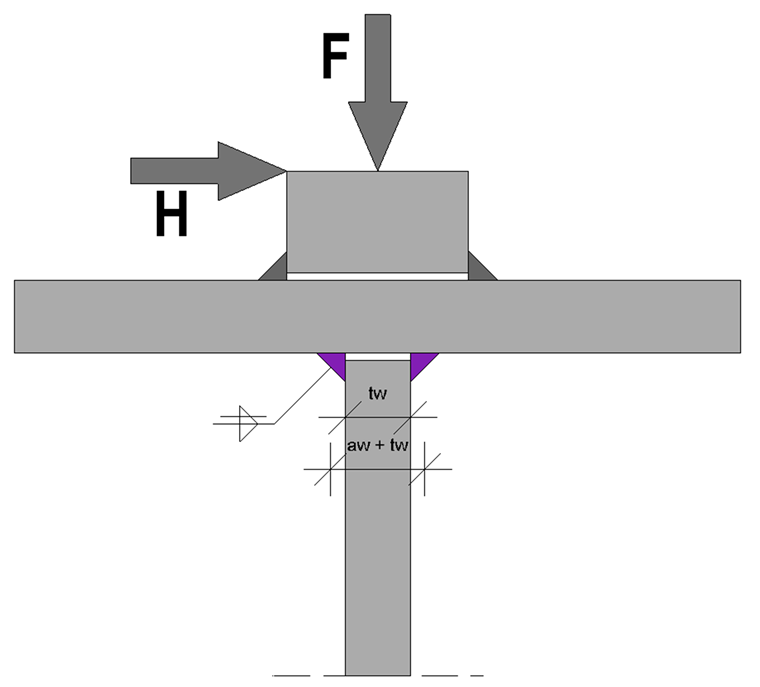
Působící zatížení vyvolávají vodorovná i svislá kolová zatížení, která je třeba zohlednit při posouzení. Excentrické kolové zatížení se při posouzení mezního stavu únosnosti neuvažuje, a nevzniká tak žádný další krouticí moment.
V následujícím textu představíme sadu vzorců pro výpočet napětí a posouzení.
Napětí od kolového zatížení
Posouzení svaru
Mezní stav únavy
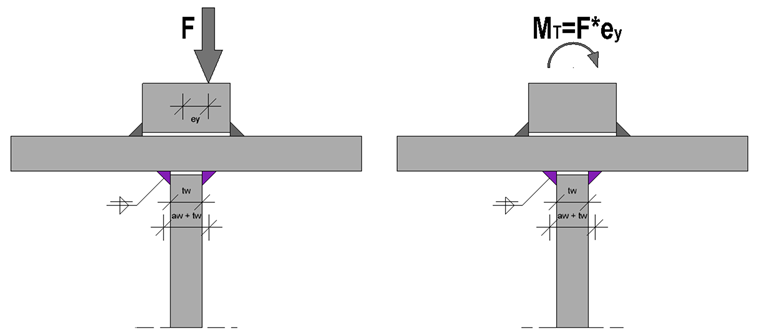
Na rozdíl od MSÚ jsou napětí od vodorovných zatížení zanedbána; Přitom se zohledňují pouze svislá kolová zatížení. V závislosti na použité třídě poškození a použité Národní příloze je ovšem třeba zohlednit excentrické kolové zatížení odpovídající 1/4 šířky hlavy kolejnice. Vzniká tak přídavný krouticí moment, který musí přenášet nejdříve svary kolejnic a následně horní pásnice, stojina a nakonec svary stojiny.
Kolejové svary musí tento krouticí moment přenášet téměř celý. Na druhé straně je třeba u svarů na stojině zohlednit vliv torzní tuhosti horní pásnice, protože to má zásadní vliv na ohyb stojiny a tím i na napětí ve svaru.
Při stanovení torzní konstanty horní pásnice se uvažuje pouze horní pásnice [2] , pokud kolejnice není pevně uložena. Pouze v takovém případě se stanoví krouticí moment od kolejnice a pásnice. Další postup je popsán v [5] , kde se sčítají jednotlivé složky torzní tuhosti kolejnice a pásnice, aby bylo možné dosáhnout vyšší tuhosti horní pásnice. Tento přístup ovšem není v [2] stanoven.
Pro posouzení koutových svarů stojiny je třeba kombinovat dvě složky napětí. K dispozici jsou přitom napětí od centrického kolového zatížení a napětí od krouticího momentu. Plný krouticí moment MT je částečně přenášen horní pásnicí; komponenta Mstojina v důsledku ohybu stojiny tak zůstává pro posouzení svaru.
Nakonec je třeba poznamenat, že tento postup výpočtu a popis se vztahuje pouze na dvojité koutové svary mezi horní pásnicí a stojinou. Pokud mají být svary na dolní pásnici a stojině také provedeny jako koutové svary, jsou účinky kolového zatížení vzhledem k existující délce působícího kolového zatížení zanedbatelně malé. V tomto případě jsou rozhodující složky napětí od ohybu nebo smykového napětí a také minimální tloušťky.
V následujícím textu představíme sadu vzorců pro výpočet napětí a posouzení.
Napětí od středového kolového zatížení
Napětí od excentrického kolového zatížení
Výsledné napětí ve svaru
Posouzení
Závěr
Tři odborné články o různých svarech nosníků jeřábů toto téma podrobně vysvětlují. Při praktickém použití v jednotlivých případech by se mělo zejména rozhodnout, zda se má uvažovat torzní tuhost horní pásnice jako součin jednotlivých komponent kolejnice a pásnice, nebo pouze pásnice.
Dlubal_KohlA_]_LI.jpg?mw=350&hash=21d94ec9a723c608496e9e95a21bb1309ab5067a)
.png?mw=350&hash=2b12ead9717e0abbf1c0c14bba66b0a2adcaed73)
DIN EN 1993-6/NA:2010-12 (Německo) 
NBN EN 1993-6/ANB:2011-03 (Belgie) 
SFS EN 1993-6/NA:2010-03 (Finsko) 
NF EN 1993-6/NA:2011-12 (Francie) 
UNI EN 1993-6/NA:2011-02 (Itálie) 
LST EN 1993-6/NA:2010-12 (Litva) 
NEN EN 1993-6/NB:2012-05 (Nizozemsko) 
NS EN 1993-6/NA:2010-01 (Norsko) 
SS EN 1993-6/NA:2011-04 (Švédsko) 
ČSN EN 1993-6/NA:2010-03 (Česká republika) 
BS EN 1993-6/NA:2009-11 (Velká Británie) 
CYS EN 1993-6/NA:2009-03 (Kypr) 
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
