Grenzzustand der Tragfähigkeit
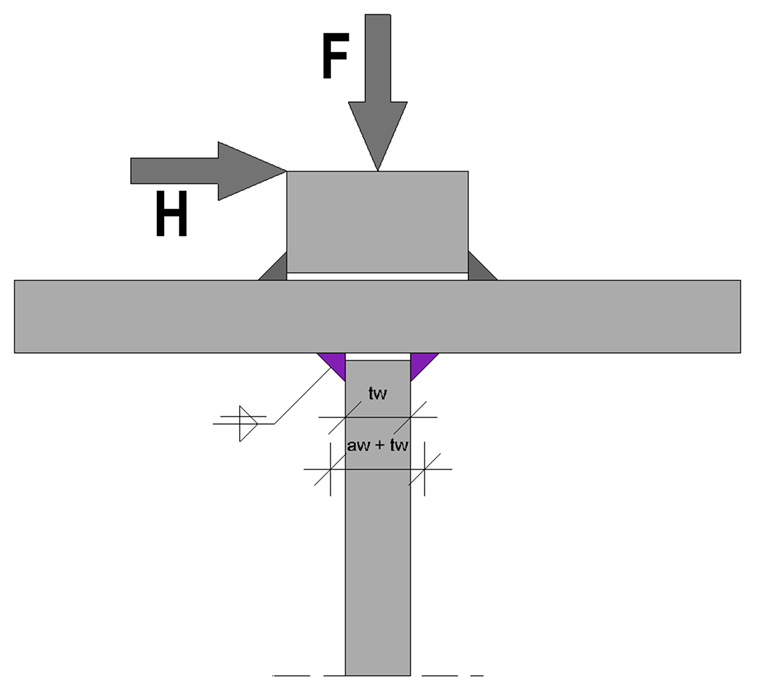
Aufgrund der anzusetzenden Belastungen ergeben sich sowohl horizontale als auch vertikale Radlasten, die in der Bemessung berücksichtigt werden müssen. Ein exzentrischer Radlastangriff der vertikalen Radlasten findet im Grenzzustand der Tagfähigkeit keine Berücksichtigung und daher ergibt sich auch kein zusätzliches Torsionsmoment.
Nachfolgend findet sich eine Zusammenstellung der Formeln zur Berechnung der Spannungen und des Nachweises.
Spannungen aus Radlastbeanspruchung
Schweißnahtnachweise
Grenzzustand der Ermüdung
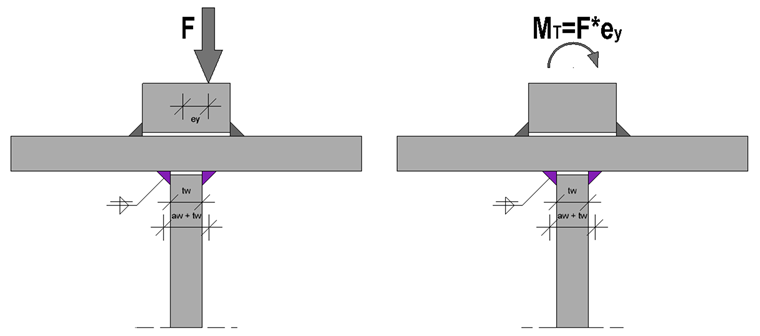
Im Gegensatz zum GZT werden die Beanspruchungen aus horizontaler Belastung vernachlässigt und somit nur die vertikalen Radlasten berücksichtigt. In Abhängigkeit der vorhandenen Schadensklasse und des verwendeten nationalen Anhanges ist jedoch der exzentrische Radlastangriff von 1/4 der Schienenkopfbreite zu berücksichtigen. Dadurch ergibt sich ein zusätzliches Torsionsmoment, welches zuerst durch Schweißnähte der Schiene und weiterhin über den Obergurt, Steg und abschließend durch die Stegnähte abgetragen werden muss.
Die Schienenschweißnähte müssen dieses Torsionsmoment nahezu komplett übertragen. Für die Schweißnähte am Steg hingegen sollte der Einfluss der Torsionssteifigkeit des Obergurtes berücksichtigt werden, da dieser die Stegbiegung, und damit verbunden die Spannung in der Schweißnaht, maßgeblich beeinflusst.
Für die Ermittlung des Torsionsträgheitmomentes des Obergurtes wird in [2] generell nur vom oberen Flansch ausgegangen, sofern die Schiene nicht schubstarr verbunden ist. Nur dann wird das Torsionsmoment aus Schiene und Flansch ermittelt. Ein weiterer Ansatz wird in [5] dargestellt, wo die einzelnen Anteile der Torsionssteifigkeiten von Schiene und Flansch addiert werden und somit eine höhere Steifigkeit des Obergurtes erzielt werden kann. Dieser Ansatz findet jedoch in [2] keine Berücksichtigung.
Für die Bemessung der Steghalsnähte müssen nun also zwei Spannungskomponenten zusammengeführt werden. Es ergeben sich Spannungen aus zentrischer Radlast und Spannungen aus Torsionsmoment. Das volle Torsionsmoment MT wird dabei teilweise durch den Obergurt aufgenommen und somit bleibt hier der Anteil MSteg aus der Stegbiegung übrig für die Bemessung der Schweißnähte.
Abschließend ist anzumerken, dass dieser Berechnungsablauf und die Erläuterungen nur für die Doppelkehlnähte zwischen oberem Flansch und Steg gelten. Sollten auch die Schweißnähte am unterem Flansch und Steg als Kehlnähte ausgebildet werden, sind die Einflüsse aus Radlast durch die vorhandene Radlasteinleitungslänge vernachlässigbar klein. Hier sind die Spannungskomponenten aus Biege - beziehungsweise Schubspannung sowie die Mindestdicken maßgebend.
Nachfolgend findet sich eine Zusammenstellung der Formeln zur Berechnung der Spannungen und des Nachweises.
Spannungen aus zentrischer Radlast
Spannungen aus exzentrischer Radlast
Resultierende Spannung in der Schweißnaht
Nachweise
Zusammenfassung
Durch diese drei Fachbeiträge zum Thema Schweißnähte an den unterschiedlichen Stellen von Kranbahnträgern ist dieses Thema ausführlich behandelt. Besonders der Ansatz der Torsionssteifigkeit des Obergurtes als Addition der einzelnen Anteile aus Schiene und Flansch oder nur des Flansches sollte in der praktischen Umsetzung im Einzelfall entschieden werden.
Dlubal_KohlA_]_LI.jpg?mw=350&hash=21d94ec9a723c608496e9e95a21bb1309ab5067a)
.png?mw=350&hash=2b12ead9717e0abbf1c0c14bba66b0a2adcaed73)
DIN EN 1993-6/NA:2010-12 (Deutschland) 
NBN EN 1993-6/ANB:2011-03 (Belgien) 
SFS EN 1993-6/NA:2010-03 (Finnland) 
NF EN 1993-6/NA:2011-12 (Frankreich) 
UNI EN 1993-6/NA:2011-02 (Italien) 
LST EN 1993-6/NA:2010-12 (Litauen) 
NEN EN 1993-6/NB:2012-05 (Niederlande) 
NS EN 1993-6/NA:2010-01 (Norwegen) 
SS EN 1993-6/NA:2011-04 (Schweden) 
CSN EN 1993-6/NA:2010-03 (Tschechische Republik) 
BS EN 1993-6/NA:2009-11 (Vereinigtes Königreich) 
CYS EN 1993-6/NA:2009-03 (Zypern) 
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
