Hypothèses pour le calcul manuel
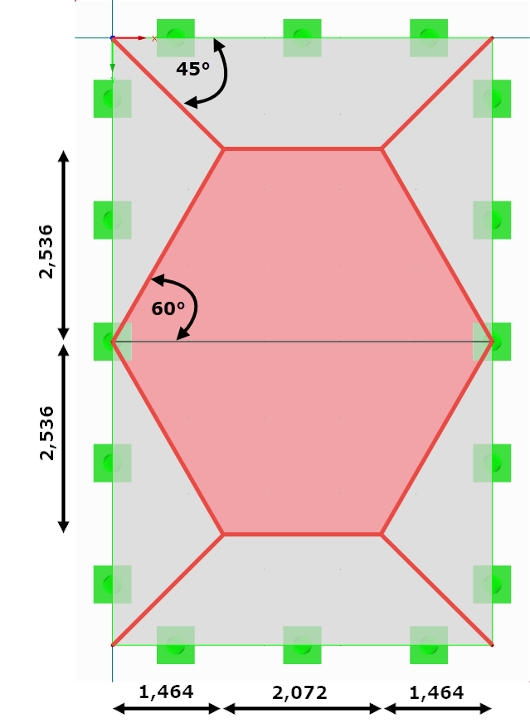
Pour les modèles calculés manuellement, les charges de barre triangulaires ou trapézoïdales des retombées de poutre sont déterminées à l’aide des zones d’application de charge et des tableaux. Une distinction est simplement faite sur l’assemblage de la plaque et de la ligne (de contour) correspondante. Si cette plaque est continue, elle est considérée comme un maintien sur la ligne, mais si cette plaque se termine sur cette ligne, il s’agit alors d’un assemblage articulé. Au point d’intersection de deux lignes perpendiculaires possédant les mêmes propriétés d’assemblage (articulé ou rigide), l’inclinaison de la distribution de charge est de 45°. Si les lignes sont perpendiculaires entre elles et ont des propriétés d’assemblage différentes, la ligne de division est inclinée à 60°. La ligne avec le maintien reçoit une plus grande charge en raison de sa rigidité supérieure. Les appuis partiellement restreints peuvent être considérés avec un angle compris entre 45° et 60°. Si la ligne parallèle opposée est suffisamment éloignée de la ligne considérée, on obtient une charge triangulaire. Si la distance à la ligne opposée est relativement faible, la charge est alors trapézoïdale.
Cette approche est indépendante de la rigidité de la barre, ce qui signifie que la charge supposée reste la même quelle que soit la taille de la retombée de poutre. De plus, la connexion de cisaillement entre la plaque et la retombée de poutre ainsi que le transfert de charge dû à la plaque sont négligés. L’effet favorable de l’excentrement n’est pas pris en compte non plus.
Exemple de calcul d’une retombée de poutre
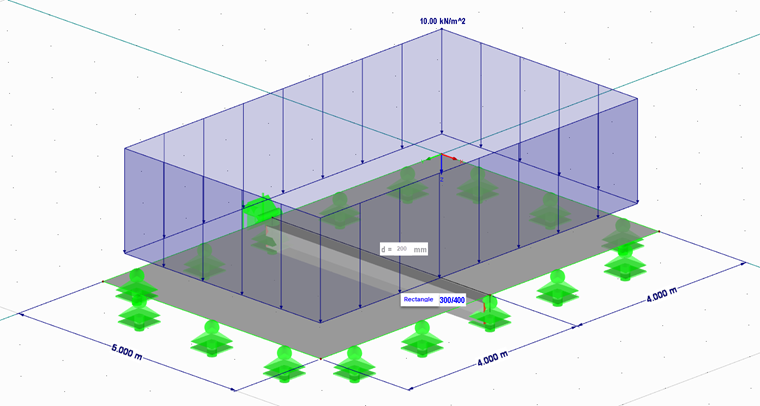
Une dalle de 20 cm d’épaisseur avec appuis articulés et des dimensions de 5 m par 8 m doit être consolidée au centre par une retombée de poutre avec une section de 30 cm · 40 cm. Seul un exemple de charge totale de 10 kN/m² sans considérer le poids propre doit s’exercer.
Calcul manuel selon l’ouvrage « Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen » de K.J. Schneider
Étant donné que la dalle s’étend sur la retombée de poutre, la charge de la barre est supposée entrée avec un angle de 60°.
Ordonnée de charge maximale d’une charge trapézoïdale :
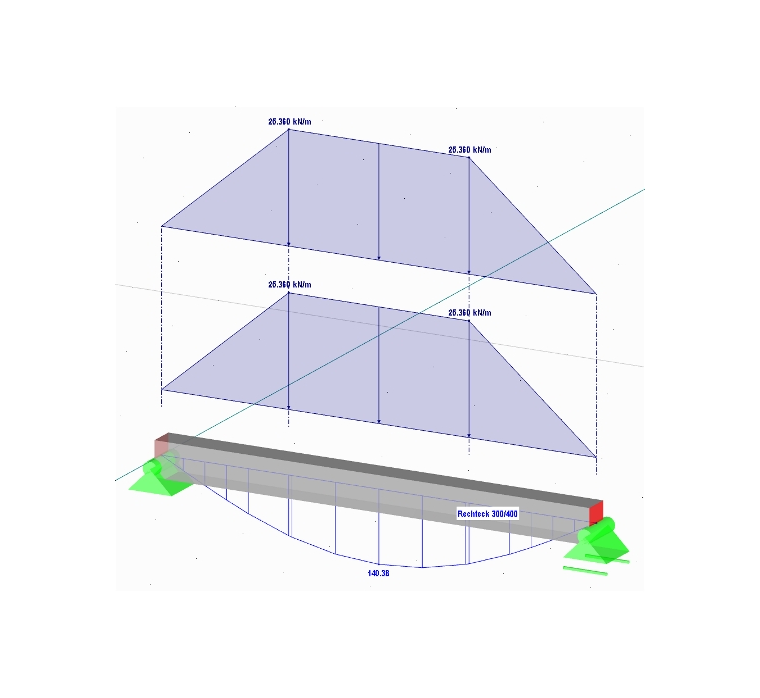
0,634 · 10 kN/m² · 4,00 m = 25,36 kN/m
Les deux travées présentent les mêmes conditions aux limites, la charge doit donc être doublée. La charge est d’abord de 0 kN/m en début de barre, puis augmente jusqu’à l’ordonnée maximale de charge sur une longueur de 0,366 × 4,00 m = 1,464 m. Si la retombée de poutre est sollicitée de cette manière, il en résulte un moment maximal en travée de My = 140,38 kNm.
Calcul dans RFEM
Pendant la modélisation, la retombée de poutre a été réglée de manière excentrée. Le bord supérieur de la barre est relié au bord inférieur de la surface. Tous les appuis linéiques transfèrent uniquement des efforts verticaux. Afin que le système ne devienne pas cinématique, un appui nodal avec un renfort dans les directions X et Y ainsi qu'avec un maintien en rotation autour de Z a été défini dans un nœud. La charge a été supposée comme charge surfacique de 10 kN/m².
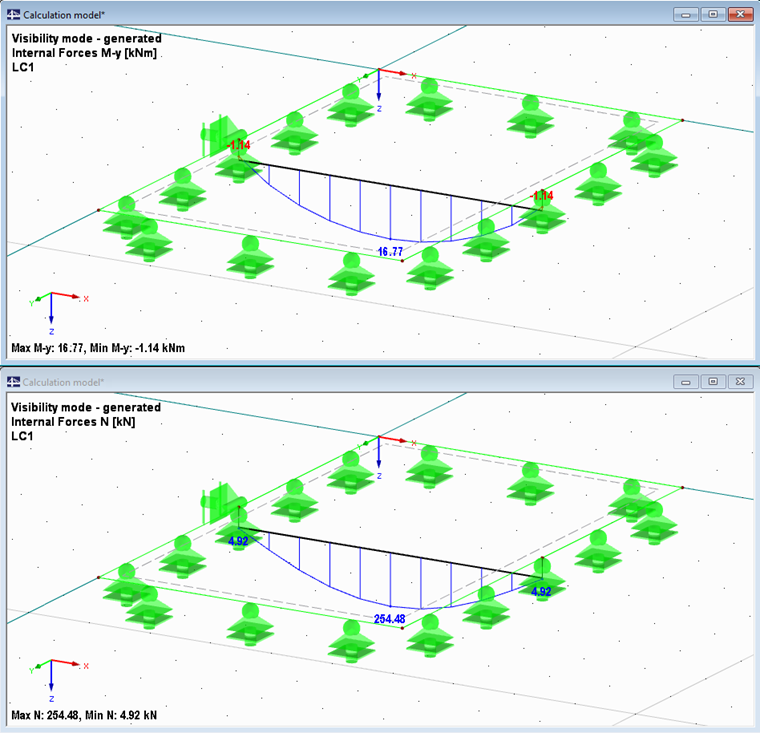
On obtient le résultat My = 16,77 kNm.
Il est cependant à noter qu’outre le moment de flexion, on obtient une distribution de l’effort normal où max N = 254,48 kN affine par rapport à la distribution des moments. Cela est dû au fait que la sollicitation n’est en effet pas seulement transférée par flexion, mais également par deux types d’effort (compression dans la plaque, traction dans la barre). Elle atteint sa valeur maximale au milieu de la travée et diminue vers le bord en effectuant une parabole.
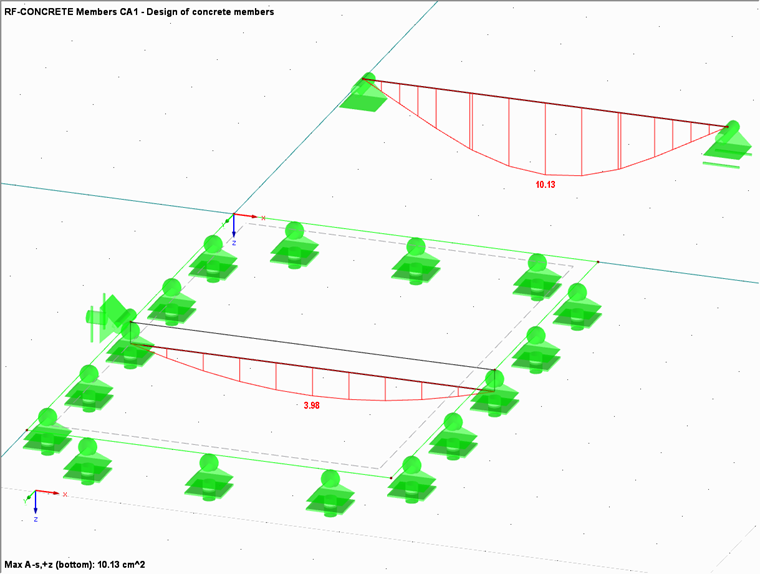
Si une vérification du béton armé est effectuée pour les deux barres, la barre simple nécessite une armature de travée inférieure de 10,13 cm², tandis que 3,98 cm² suffisent pour la « véritable » retombée de poutre.
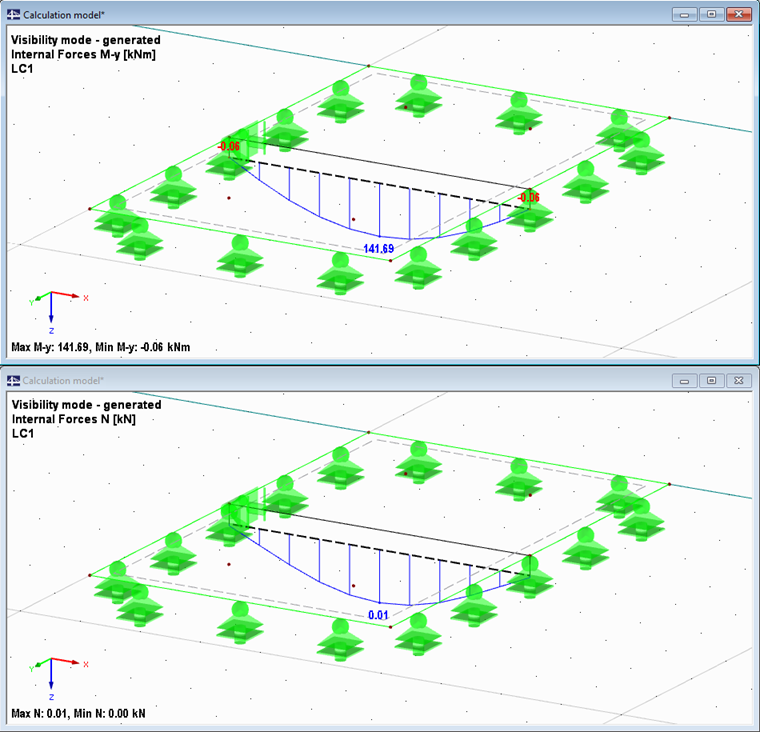
Pour vérifier le calcul manuel, le système mixte est copié et une barre rigide est utilisée à la place des dimensions réelles de la section. Dans ce système, on obtient un moment fléchissant maximal de 141,69 kNm, ce qui est similaire à celui du calcul manuel (140,38). L’effort normal de 0,01 kN peut être négligé.
Conclusion
Le calcul manuel fournit des résultats cohérents par rapport à ceux du calcul aux éléments finis pour les retombée de poutre très rigides ou pour la détermination des efforts des appuis verticalement non déplaçables. Des logiciels d’analyse aux éléments finis doivent cependant être utilisés pour obtenir des résultats plus précis et plus économiques. Outre la surestimation des efforts internes de barre décrite ci-dessus, il en va de même pour les efforts internes de la plaque. Dans le cas d’une poutre très faible, il est possible qu’un moment positif résulte de la déformation plus importante au lieu de l’armature supposée dans le logiciels d’analyse aux éléments finis. Au lieu de l’armature d’appui appliquée (du côté supérieur de la plaque), une armature de travée (du côté inférieur de la plaque) doit être positionnée en considérant les rigidités réalistes.