Symboles :
h : Hauteur de la section
L : travée de poutre
E : Module d'élasticité
G : module de cisaillement
κ : Facteur de correction du cisaillement
A : aire de la section
w : Déformation
Le module de cisaillement faible ou le rapport G/E faible constitue un facteur décisif. Cette valeur est de 1/16 pour le bois résineux en raison de l'anisotropie selon [1]. On obtient une valeur bien plus importante pour les matériaux isotropes. Le rapport G/E s'élève par exemple à 1/2,6 pour l'acier.
Théorie des poutres
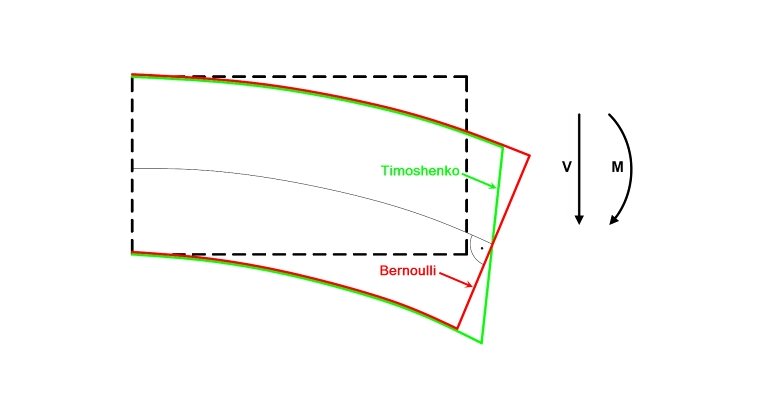
Alors que selon la théorie des poutres de Bernoulli, la section d'une barre reste perpendiculaire à l'axe de la poutre lorsqu'elle est déformée, le cisaillement est considéré dans la théorie des poutres de Timoshenko (poutre flexible). Par conséquent, la section d'une barre n'est plus perpendiculaire à l'axe de la barre lorsqu'elle est déformée (voir la Figure 01). Si l'on suppose que la section reste plane, on obtient une répartition uniforme des contraintes de cisaillement le long de la hauteur de la poutre. Un facteur de correction du cisaillement est cependant considéré pour la détermination des surfaces de cisaillement car la répartition est parabolique, ce qui correspond à un rapport de 5/6 pour une section rectangulaire. La rigidité au cisaillement d'une barre rectangulaire est exprimée par la formule suivante :
Normes
La norme n'indique pas selon quel critère les déformations de barre dues au cisaillement doivent être considérées et les ingénieurs doivent le décider eux-mêmes.
Exemple
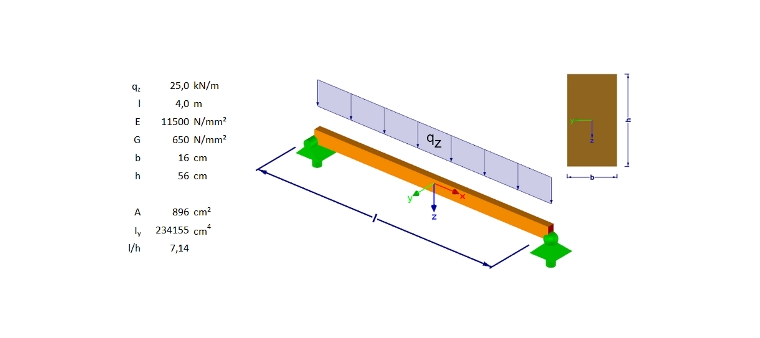
L'exemple simple décrit ici montre l'influence des déformations dues au cisaillement. On considère une poutre articulée à travée simple qui doit servir de retombée de poutre (détails sur la Figure 02).
L'objectif est d'abord de déterminer uniquement la déformation d'après la courbure du moment. La déformation caractéristique du système représenté ici est :
Le rapport de la déformation due au cisaillement peut être calculée par exemple avec le working setl ou simplifiée selon les recherches figurant dans [2] ou [3]. Pour une poutre articulée à travée simple, on obtient ainsi :
La déformation totale équivant donc à :
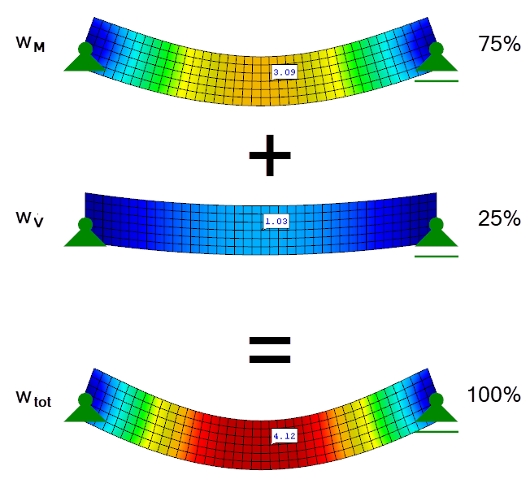
Dans cet exemple, le rapport de la déformation due au cisaillement s'élève déjà à 25 % de la déformation totale. Les différents rapports de la déformation due au cisaillement sont visibles sur la Figure 03.
Élancement
L'élancement de barre est un facteur déterminant pour la déformation due au cisaillement. Alors que les déformations sont négligeables pour les barres élancées avec un rapport L/h élevé, elles ont une influence significative sur les barres plus épaisses présentant un rapport L/h faible.
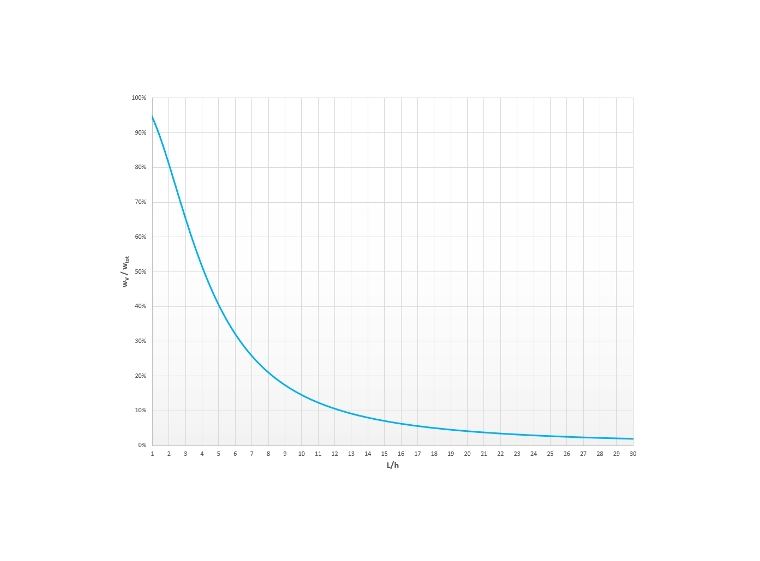
Le diagramme de la Figure 04 montre l'influence de la déformation due au cisaillement sur la déformation totale. Pour les poutres articulées à travée simple de section rectangulaire, la déformation due au cisaillement prédomine jusqu'à un rapport L/h de 4. Ce n'est qu'une fois ce rapport dépassé que le rapport de la courbure du moment prévaut. À partir d'un rapport L/h égal à 12, l'influence de la déformation due au cisaillement ne concerne plus que de 10 % de la déformation totale.
Systèmes statiques indéterminés
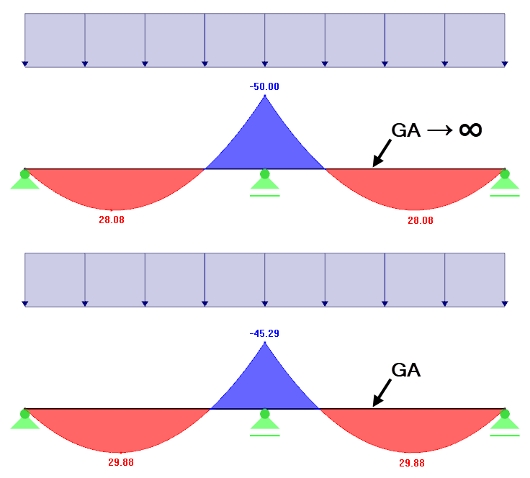
Les déformations dues au cisaillement ont une influence plus importante dans les systèmes statiques indéterminés que dans les systèmes statiques déterminés. Dans ce cas, les déformations dues à l'effort tranchant ont une influence sur le moment fléchissant et donc également sur les déformations dues à la flexion. Cette redistribution peut par exemple avoir un effet positif sur les moments d'appui (voir la Figure 05).
Déformations dues au cisaillement dans RFEM et RSTAB
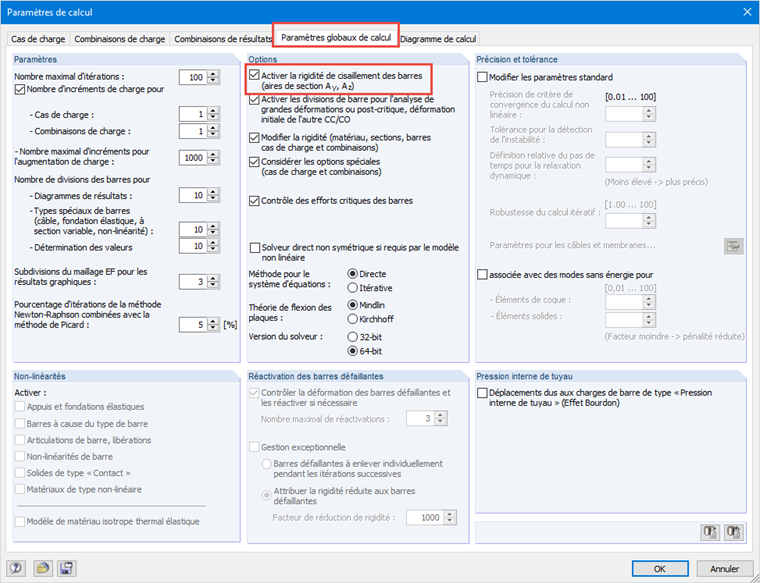
Les déformations de barre dues au cisaillement sont automatiquement considérées dans RFEM et RSTAB. Toutefois, elles peuvent également être négligées lors des calculs de contrôle à l'aide de la fonction indiquée sur la Figure 06. Si cette case est cochée, les déformations dues au cisaillement sont prises en compte. Sinon, seuls les rapports de déformation du moment fléchissant sont considérés.
Résumé
Dans de nombreux cas, les déformations dues au cisaillement peuvent être négligées car elles ont un impact limité sur la déformation totale. Cela ne doit toutefois pas être le cas pour des barres épaisses. Alors que les déformations due au cisaillement sont toujours considérées par défaut dans RFEM et RSTAB, des outils doivent être utilisés pour effectuer les calculs manuels (voir [2] ou [3]).
Base de connaissance