Présentation
Lors du calcul de barres en béton armé selon l'ACI 318-19 [1], le diagramme d'interaction des moments est un outil essentiel. Ces diagrammes représentent la relation entre le moment fléchissant et l'effort normal en un point donné le long d'une barre en béton armé. Des informations précieuses sont affichées visuellement, telles que la résistance et le comportement du béton dans différentes conditions de charge.
Explication
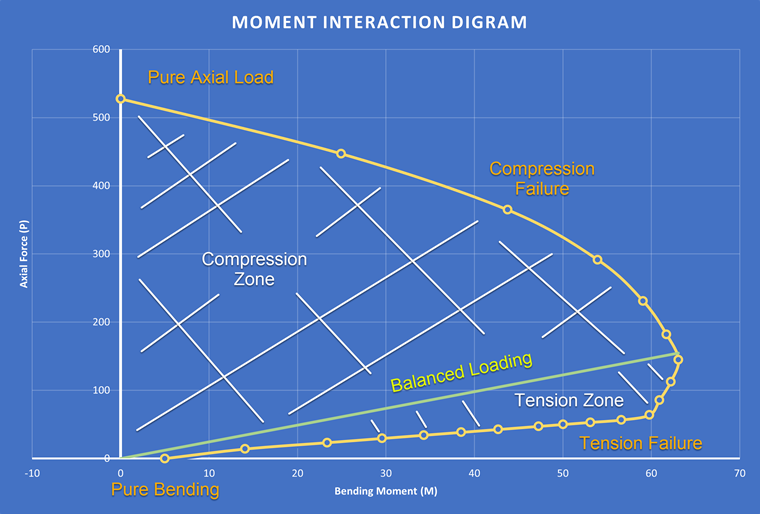
Le diagramme d'interaction des moments est utilisé pour déterminer le moment et l'effort normal maximum auxquels une barre peut résister, ce qui est utile pour calculer la résistance ultime. La génération d'un diagramme d'interaction des moments nécessite le calcul de l'effort normal et du moment maximaux. Ces points sont ensuite tracés sur un graphe xy. L'axe des y représente l'effort normal et l'axe des x le moment fléchissant. L'interaction entre ces deux forces est représentée par une ligne/courbe qui représente la résistance maximale de la section renforcée. Tout point de la courbe représente une combinaison unique de moment fléchissant et d'effort normal à laquelle la section renforcée peut résister. Cette courbe est ensuite divisée en régions en fonction des points de rupture. Par exemple, la zone supérieure représente une rupture en flexion pure et la zone inférieure représente une rupture axiale pure. Cela est montré dans la Figure 01.
Intégration dans RFEM 6
Grâce au module complémentaire Vérification du béton, RFEM 6 permet d'analyser et de calculer des structures en béton armé. Le module complémentaire permet de créer automatiquement un diagramme d'interaction des moments pour n'importe quel poteau ou poutre. Le moment et l'effort normal maximum auxquels une barre peut résister sont calculés dans l'analyse statique qui est automatiquement considérée dans le module complémentaire Vérification du béton. Ensuite, une fois l'option cochée, un diagramme d'interaction des moments est généré sur la base de propriétés telles que la taille de la section et la disposition des armatures.
Vérification analytique
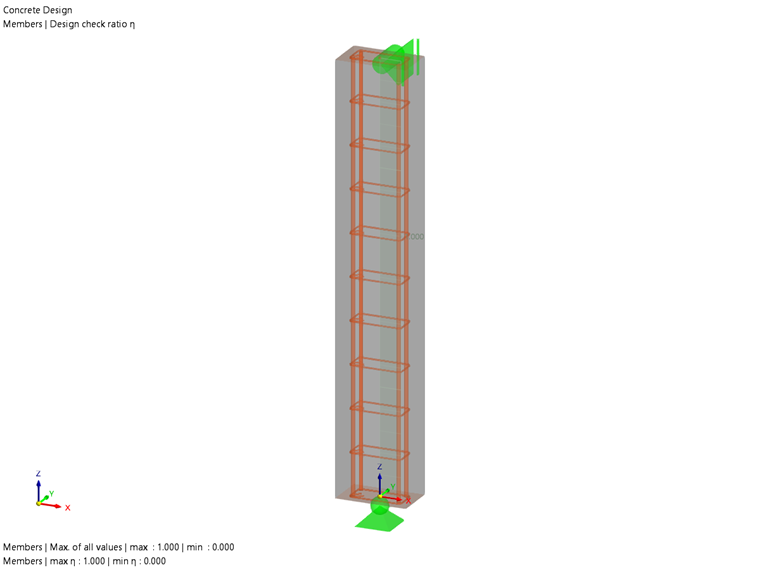
Un poteau rectangulaire en béton armé de 12" x 20" est modélisé et montré dans la Figure 02.
Le poteau en béton de 3 m a une résistance à la compression (f'c) égale à 4 000 psi. Quatre barres d'armatures de diamètre 9, de nuance 60 sont placées dans les coins pour l'armature longitudinale. Les barres de diamètre 4 sont sélectionnées pour l'armature d'effort tranchant. L'enrobage de béton est de 2,5 pouces.
Pour cette section, un diagramme d'interaction linéaire à 4 points sera calculé analytiquement et vérifié avec RFEM 6.
Les profondeurs de l'armatures de traction et de compression sont calculées comme suit :
d = 20" - 2,5" = 17,5"
d' = 2,5"
Le point A est le premier. On suppose que la barre subit une compression pure et que la section a atteint la déformation limite (εcu) de 0,003. Les résistances en compression de l'acier et du béton sont additionnées ci-dessous. Le point de compression pure, basé sur le diagramme contrainte-déformation, est calculé ci-dessous :
L'effort normal (PN,A) est égal à 1042,4 kips.
Comme seule la compression pure est présente, le moment (MN,A) est égal à 0 kip-in.
Le point B est le suivant. Il s'agit du point « d'équilibre » où nous supposons que l'acier fléchi. Ceci doit être vérifié. Les « triangles similaires » sont utilisés pour calculer l'axe neutre ou la longueur de la partie en compression (c). Pour référence, c pour le point A était égal à 20 pouces car toute la section était en compression.
c est égal à 10,36 pouces. Maintenant que c est connu, la déformation de l'acier en compression (ε's) est calculée et comparée à la déformation élastique de l'acier de nuance 60.
(ε's) est égal à 2,27x10-3, ce qui est supérieur à 2,07x10-3. L'hypothèse était donc correcte. La résistance axiale en ce point, basée sur le diagramme des contraintes, est calculée :
PN,B est égal à 359 kips.
Le moment MN,B est calculé et additionné autour de l'axe neutre :
MN,B est égal à 3940,23 kip-in.
Le point C est maintenant calculé là où l'effort normal PN,C est égal à 0. La section est supposée doublement renforcée, mais l'acier comprimé est négligé. L'effort normal est égal à 0 kips et le moment est calculé comme suit :
MN,C est égal à 1923,53 kip-in.
Le point D est le dernier où MN,D est égal à 0 kips et seul l'effort normal pur se produit.
PN,D est égal à 240 kips.
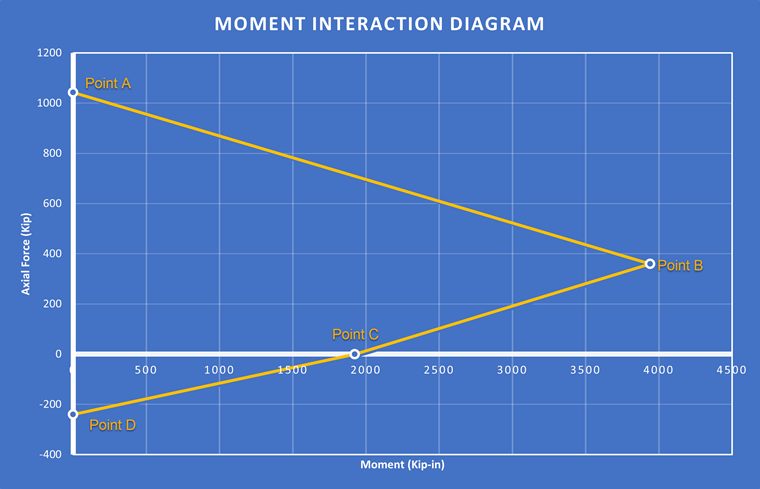
Ces points sont tracés, créant ainsi un diagramme d'interaction des moments linéaires. Ceci est montré dans l'image 02 ci-dessous :
Vérification dans RFEM 6
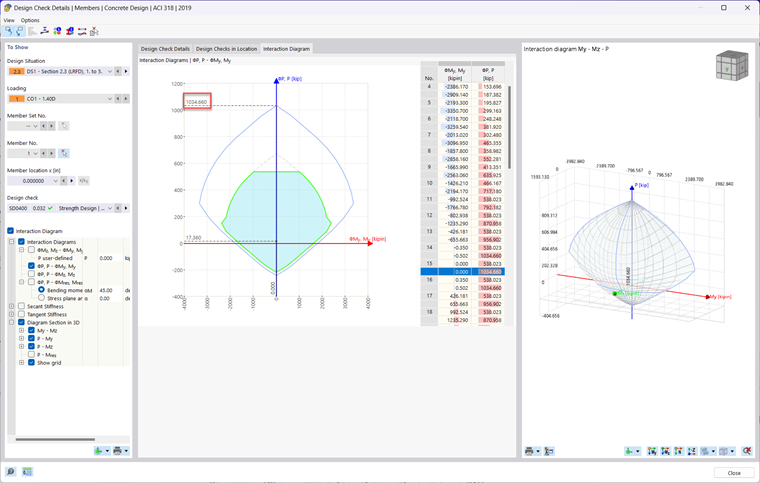
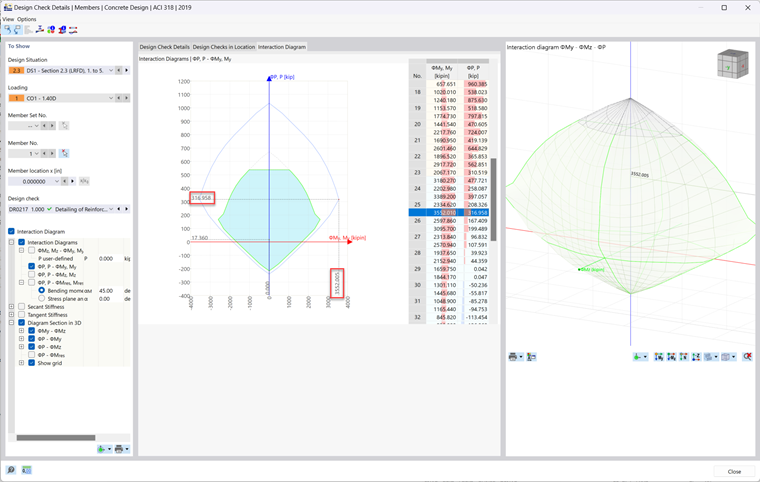
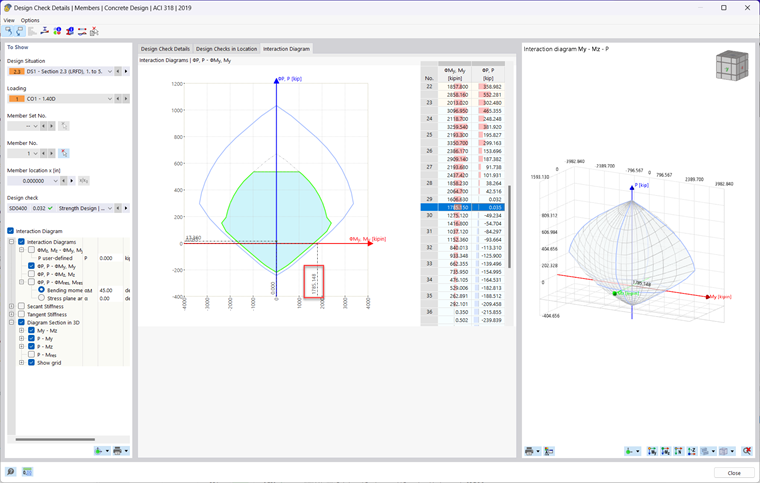
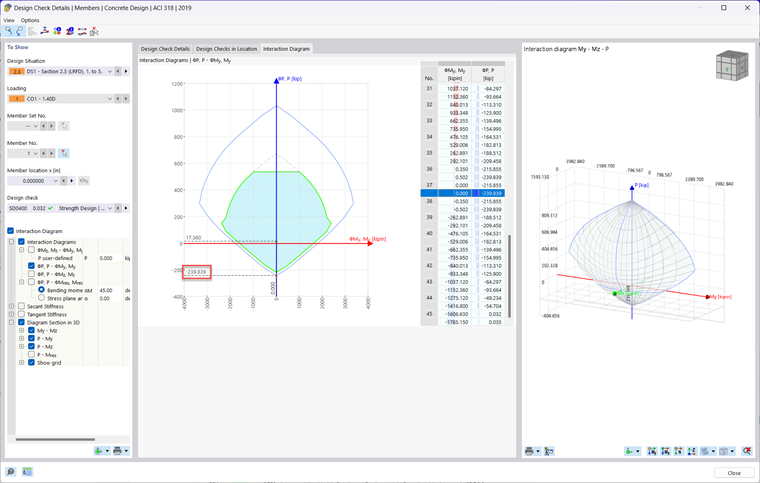
Pour afficher le diagramme d'interaction des moments généré par le module complémentaire Vérification du béton dans RFEM 6, exécutez simplement les résultats de la vérification dans le tableau. Cliquez ensuite sur le bouton Détails de vérification dans le tableau ou double-cliquez sur une vérification. Cochez ensuite la case Diagramme d'interaction. Un nouvel onglet apparaît alors dans la partie supérieure où vous pouvez afficher les diagrammes d'interaction des moments 2D et 3D de la barre en cours de calcul.
La barre a été extraite de l'exemple analytiquement vérifié ci-dessus et modélisée dans RFEM 6. La section, les matériaux et la disposition des barres d'armature ont été reproduits. Le calcul est effectué à l'aide du module complémentaire Vérification du béton selon la norme ACI 318-19 [1]. Le rendu de barre est montré dans la Figure 03 et les résultats sont comparés et vérifiés ci-dessous. Les points A à D sont affichés dans les images 4 à 8 avec un rapport de vérification comparant le résultat analytique au résultat de RFEM 6.
Remarque : RFEM 6 suppose un diagramme de contraintes parabolique alors que l'exemple analytique suppose un diagramme de contraintes rectangulaire. La différence entre le diagramme des moments analytique et le diagramme des moments de RFEM 6 réside dans les hypothèses émises concernant le comportement des matériaux et la distribution des moments résultante. Le diagramme de contrainte analytique suppose un comportement linéaire du béton, tandis que le diagramme de contrainte de RFEM 6 considère une distribution des contraintes non linéaire dans le béton. Le diagramme des contraintes de RFEM 6 fournit une représentation plus précise du comportement de la section. La comparaison de l'exemple analytique avec les résultats de RFEM 6, que l'on peut voir ci-dessous, entraîne donc des écarts de résultats.
Rapport du point A :
PN,A = 1,007
MN,A = 1,000
Rapport du point B :
PN,B = 1,133
MN,B = 1,109
Rapport du point C :
PN,C = 1,000
MN,C = 1,043
Rapport du point D :
PN,D = 1,001
MN,D = 1,000
Conclusion
Le diagramme d'interaction des moments est un outil essentiel pour les ingénieurs qui calculent le béton armé. Ces diagrammes fournissent des détails importants sur la résistance, la stabilité et le comportement du béton dans diverses conditions de charge. RFEM 6 est un outil précieux qui peut être utilisé pour générer des diagrammes d'interaction des moments et les afficher en temps réel.