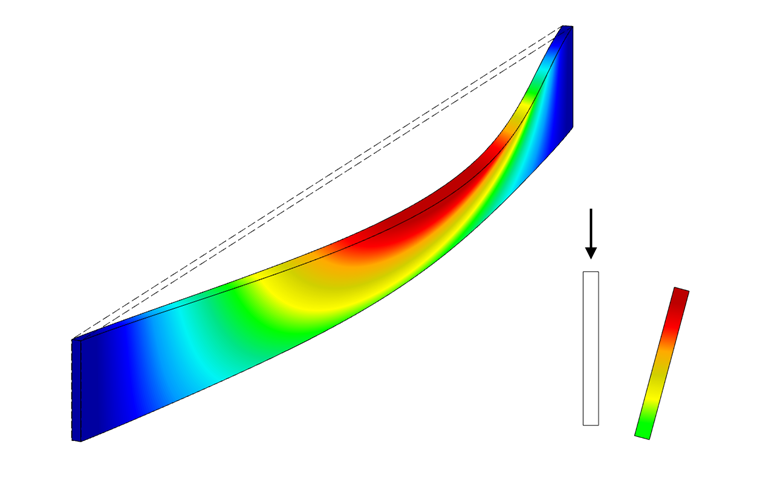
La viga tiene un desplazamiento lateral con rotación simultánea (ver Figura 01). Esto se llama pandeo lateral o vuelco lateral. Similar al pandeo por flexión, donde una barra se dobla repentinamente cuando se alcanza la carga de Euler, el cordón comprimido se desplaza a partir de una carga de pandeo lateral crítica durante el vuelco lateral. Esto da como resultado un momento crítico de flexión Mcrit, que da como resultado una tensión crítica para el vuelco lateral σcrit.
Símbolos utilizados:
| L | Longitud de la viga |
| E | Módulo de elasticidad |
| Módulo de cortante | |
| Iz | momento de inercia respecto al eje débil |
| IT | Módulo de torsión |
| Iω | Resistencia al alabeo |
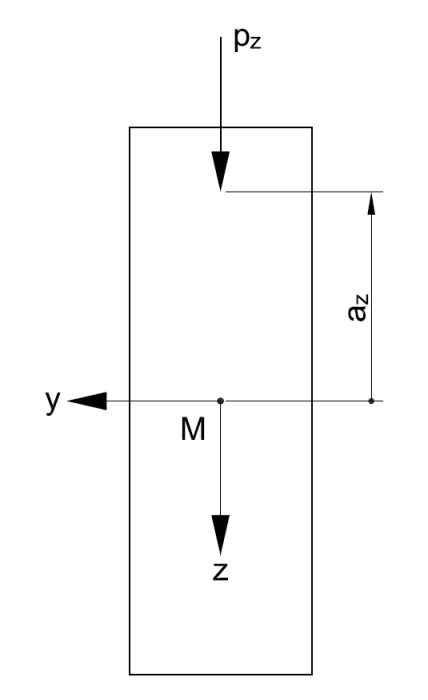
| az | distancia de aplicación de carga desde el centro de cortante |
| e | distancia del apoyo elástico en la barra desde el centro de corte |
| K | muella a torsión elástico en apoyo en Nmm |
| Kθ | coacción al giro elástica en N |
| Ky | apoyo elástico en barra en N/mm² |
Determinación analítica de Mcrit
Para determinar el momento flector donde una viga se vuelve inestable, el calculista puede usar las soluciones analíticas de la bibliografía, pero estas son limitadas en su aplicación. En [1], se deriva la siguiente ecuación para una viga de vano simple con coacciones laterales y torsionales y articulada en ambos lados, con un momento flector y una aplicación de carga constantes en el centro de cortante.
En el caso de secciones no deformables (por ejemplo, una sección rectangular estrecha en una construcción de madera), la rigidez de alabeo se puede establecer en cero y, por lo tanto, se omite la parte en el paréntesis.
Dado que hay muchos más casos en el análisis estructural que los mencionados anteriormente, se han introducido factores de corrección para tener en cuenta, por ejemplo, las distribuciones de momentos desviados, las situaciones de apoyo y una aplicación de carga diferente. Para esto, la longitud de la viga se modifica con los factores y da como resultado una longitud eficaz lef. Esto se describe en [2], entre otros, de la siguiente manera.
az es la distancia de la aplicación de carga desde el centro de cortante.
Si la carga actúa en el lado inferior de la viga, se debe considerar az con signos negativos. Los coeficientes a1 y a2 se muestran en la figura 03.
Los sistemas distintos deben entenderse de la manera siguiente:
- Viga de un vano con coacciones laterales y de torsión y articuladas en ambos lados
- Viga coaccionada
- Voladizo con coacción lateral y torsional en el extremo libre
- Viga fija en ambos lados
- Viga de un vano con coacción en un lado
- Viga de dos vanos
- Viga continua con coacción lateral y torsional - vano interior
- Viga continua con coacción lateral y torsional - vano exterior
Las normas proponen el cálculo del vuelco lateral según el método de la barra equivalente. Se debe calcular el momento crítico con los valores de un cuantil del 5% de las rigideces. Por lo tanto, resulta lo siguiente para estructuras de madera:
La tensión crítica de flexión resulta en:
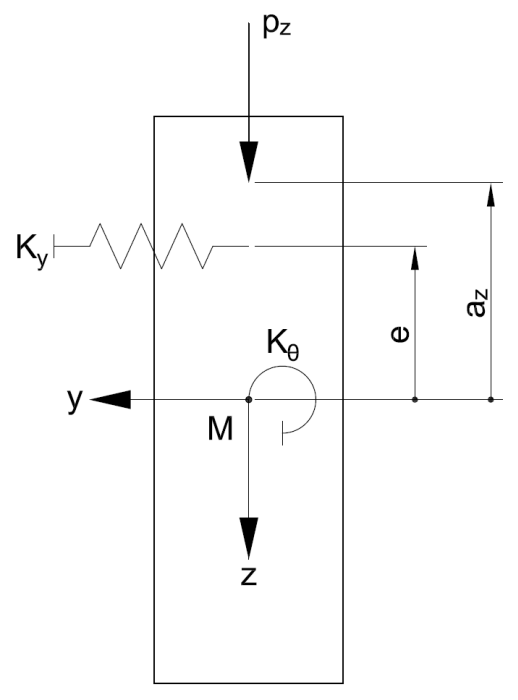
Si desea considerar un muelle a torsión elástico (por ejemplo, resultante de la flexibilidad de la coacción lateral y torsional) en el apoyo, una coacción al giro elástica (por ejemplo, de una chapa trapezoidal) o un apoyo elástico en la barra elástica (por ejemplo , de los arriostramientos), puede ampliar la ecuación anterior de la siguiente manera: [2].
Donde
Si el muelle a torsiónKG en el apoyo se considera infinitamente rígido, el resultado α = 1. La coacción al giro elástica KΘ generalmente no se considera en la construcción de madera, ya que no hay estudios. Por lo tanto, el parámetroKΘ se incluye en la ecuación con el valor 0. El apoyo elástico de la barra elástica Ky, resultante de un arriostramiento o un panel de cortante, tiene un efecto favorable en el comportamiento de pandeo lateral de una viga. Sin embargo, tenga en cuenta que la ecuación anterior tiene una aplicación limitada. Estrictamente hablando, solo es válido si hay una flecha en un gran arco sinusoidal. Si el apoyo de la barra es demasiado rígido, esto ya no se da porque la deformada del modo tiene varios arcos a lo largo de la viga. Actualmente no hay una definición de cuándo la fórmula ampliada con α y β deja de ser válida.
En el próximo artículo se describirá cómo resolver estos problemas de valores propios de una manera hábil.