Der Träger erfährt eine seitliche Verschiebung bei gleichzeitiger Verdrehung (siehe Bild 01). Hierbei spricht man von Biegedrillknicken beziehungsweise vom Kippen. Analog zum Biegeknicken, bei dem ein Stab beim Erreichen der Eulerschen Knicklast schlagartig ausknickt, weicht der Druckgurt beim Biegedrillknicken ab einer kritischen Kippbelastung aus. Daraus resultiert ein kritisches Biegemoment Mcrit, welches eine kritische Kippbiegespannung σcrit zur Folge hat.
Verwendete Symbole:
| L | Trägerlänge |
| E | Elastizitätsmodul |
| G | Schubmodul |
| Iz | Trägheitsmoment um die schwache Achse |
| IT | Torsionsträgheitsmoment |
| Iω | Wölbwiderstand |
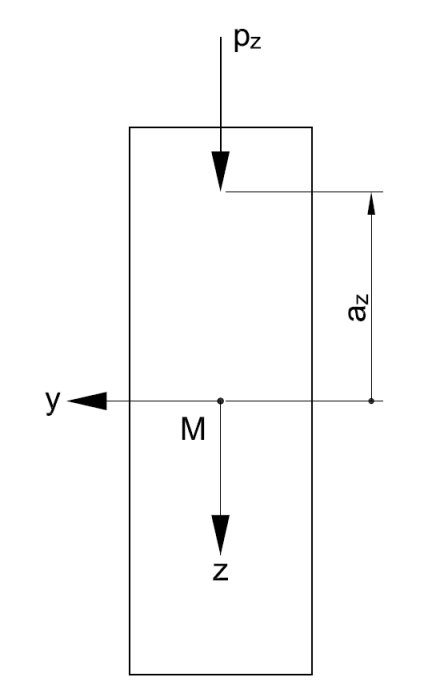
| az | Abstand des Lastangriffs vom Schubmittelpunkt |
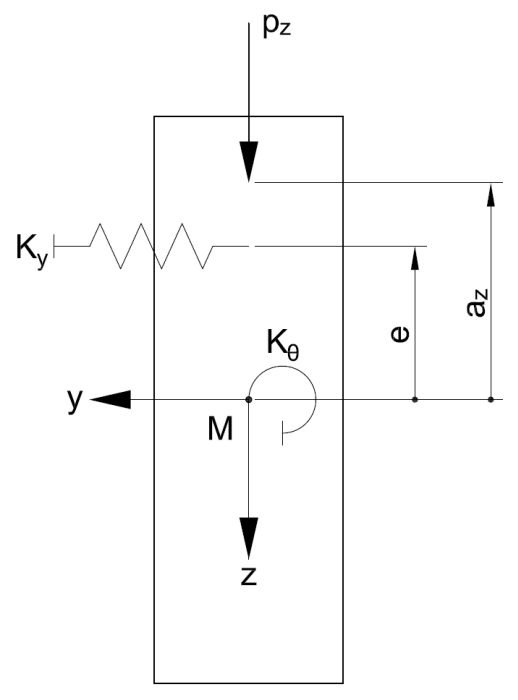
| e | Abstand der Stabbettung vom Schubmittelpunkt |
| KG | Elastische Drehfeder am Auflager in Nmm |
| KΘ | Elastische Drehbettung in N |
| Ky | Elastische Stabbettung in N/mm² |
Analytische Ermittlung von Mcrit
Um das Biegemoment zu bestimmen, unter dem ein Träger instabil wird, stehen dem Ingenieur in der Literatur analytische Lösungen zur Verfügung, die jedoch in der Anwendung eingeschränkt sind. In [1] wird für einen beidseitig gelenkig gabelgelagerten Einfeldträger mit einem konstanten Biegemoment und Lastangriff im Schubmittelpunkt folgende Gleichung hergeleitet.
Bei wölbfreien Querschnitten (zum Beispiel schmaler Rechteckquerschnitt im Holzbau) kann die Wölbsteifigkeit zu null gesetzt werden und somit entfällt der Teil in der Klammer.
Da es in der Baustatik wesentlich mehr Fälle gibt als den oben genannten, wurden Korrekturfaktoren eingeführt, um beispielsweise abweichende Momentenverläufe, Auflagersituationen und einen abweichenden Lastangriff zu berücksichtigen. Hierfür wird die Länge des Trägers mit den Faktoren modifiziert und es resultiert eine effektive Länge lef. Diese wird unter anderem in [2] wie folgt beschrieben.
Dabei ist az der Abstand des Lastangriffs vom Schubmittelpunkt.
Wirkt die Last an der Unterseite des Trägers, so ist az mit negativen Vorzeichen zu berücksichtigen. Die Beiwerte a1 und a2 sind Bild 03 zu entnehmen.
Die verschiedenen Systeme sind wie folgt zu verstehen:
- Beidseitig gelenkig gabelgelagerter Einfeldträger
- Eingespannter Träger
- Kragarm mit Gabellagerung am freien Ende
- Beidseitig eingespannter Träger
- Einfeldträger mit einseitiger Einspannung
- Zweifeldträger
- Gabelgelagerter Durchlaufträger - Innenfeld
- Gabelgelagerter Durchlaufträger - Außenfeld
In den Normen wird der Kippnachweis nach dem Ersatzstabverfahren vorgeschlagen. Dabei ist das kritische Moment mit den 5%-Quantilwerten der Steifigkeiten zu berechnen. Somit ergibt sich für den Holzbau:
Die kritische Biegespannung resultiert zu:
Soll eine elastische Drehfeder (zum Beispiel resultierend aus der Nachgiebigkeit der Gabellagerung) am Auflager, eine elastische Drehbettung (beispielsweise aus Trapezblechen) oder eine elastische Stabbettung (zum Beispiel aus Verbänden) berücksichtigt werden, so kann vorherige Gleichung wie folgt erweitert werden [2].
Dabei ist
Wird die Drehfeder KG am Auflager als unendlich steif berücksichtigt, so ergibt sich α = 1. Die elastische Drehbettung KΘ wird im Holzbau in der Regel nicht berücksichtigt, da hier keine Untersuchungen vorliegen. Der Parameter KΘ fließt somit mit dem Wert 0 in die Gleichung ein. Die elastische Stabbettung Ky, resultierend aus einem Verband beziehungsweise einem Schubfeld, wirkt sich günstig auf das Kippverhalten eines Trägers aus. Es ist jedoch zu berücksichtigen, dass die vorherige Gleichung in ihrer Anwendung eingeschränkt ist. Diese hat streng genommen nur Gültigkeit, wenn eine Auslenkung in einem großen Sinusbogen vorliegt. Ist die Stabbettung zu steif, ist dies nicht mehr gegeben, da die Eigenform entlang des Trägers mehrere Bögen aufweist. Eine Abgrenzung, ab wann die erweiterte Formel mit α und β ihre Gültigkeit verliert, existiert derzeit nicht.
Wie derartige Eigenwertprobleme geschickt gelöst werden können, wird im nächsten Beitrag an verschiedenen Beispielen erläutert.