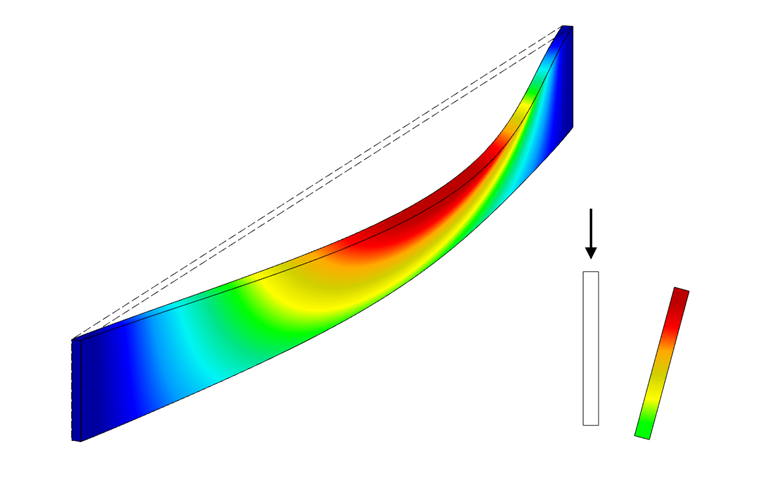
Une poutre présente un déplacement latéral avec rotation (voir la Figure 01). On parle alors de déversement ou de flambement latéral. Ce phénomène est semblable au phénomène de flambement : une barre flambe soudainement lorsque la charge critique d'Euler est atteinte. Ici, la semelle comprimée provoque le déversement à partir d'une certaine charge critique. On obtient alors un moment de flexion critique Mcrit, qui entraîne une contrainte de flexion critique σcrit.
Symboles :
| L | Longueur de la poutre |
| E | Module d'élasticité |
| G | Module de cisaillement |
| Iz | Moment d'inertie selon l'axe faible |
| IT | Inertie de torsion |
| Iω | Constante de gauchissement |
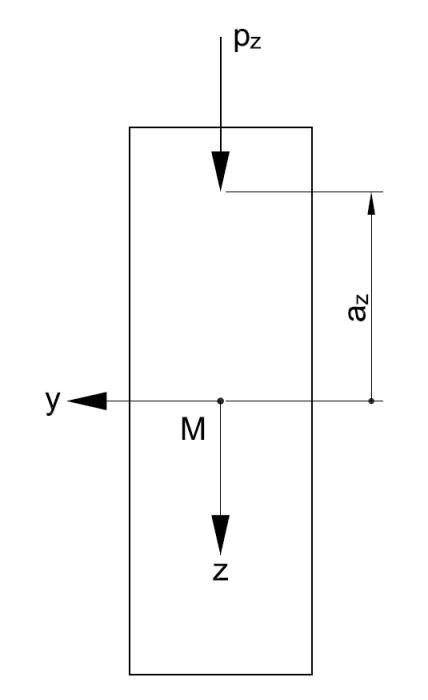
| az | Distance d'application de la charge au centre de cisaillement |
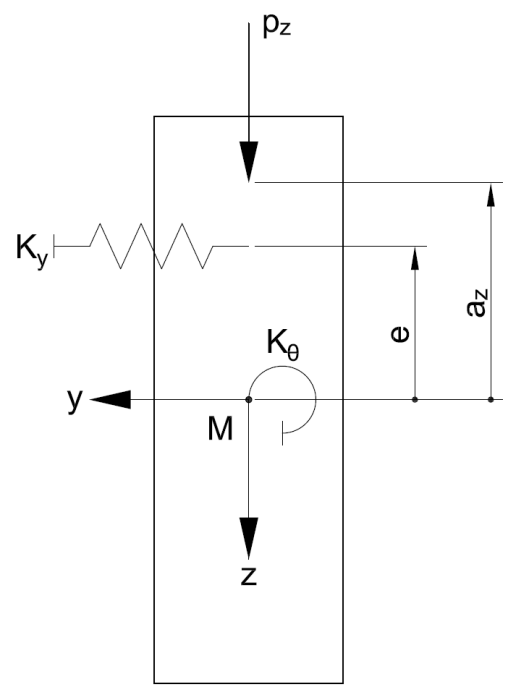
| e | Espacement entre la fondation élastique de barre et le centre de cisaillement |
| KG | Ressort de rotation élastique de l'appui en Nmm |
| Kθ | Maintien élastique en rotation en N |
| Ky | Fondation élastique de la barre en N/mm² |
Détermination analytique de Mcrit
Pour déterminer le moment fléchissant auquel une poutre devient instable, l'ingénieur peut utiliser les solutions analytiques proposées dans la littérature spécialisée, mais leur application est limitée. Dans [1], l'équation suivante est dérivée pour une poutre à travée simple et appui articulé aux extrémités avec un moment fléchissant constant et une charge appliquée au centre de cisaillement.
Dans le cas de sections sans gauchissement (par exemple, des sections rectangulaires étroites dans des constructions en bois), la rigidité de gauchissement peut être définie sur zéro et la partie entre parenthèses est omise.
Les cas traités par les ingénieurs structures étant bien plus nombreux et diversifiés que ceux mentionnés ci-dessus, des facteurs de correction ont été introduits pour considérer, par exemple, la déviation de la distribution de moments, les différents cas d'application de charge et les conditions d'appui. La longueur de la poutre est ainsi modifiée à l'aide de ces facteurs et on obtient une longueur efficace lef. Elle est donnée comme suit dans [2] :
az est l'espacement entre le point d'application de la charge et le centre de cisaillement.
Si la charge agit sur le côté inférieur de la poutre, az doit être considéré avec un signe négatif. Les coefficients a1 et a2 sont donnés sur la Figure 03.
Les différents systèmes sont les suivants :
- Poutre à travée simple sur deux appuis articulés aux extrémités
- Poutre en porte-à-faux
- Poutre en porte-à-faux avec des maintiens latéraux à l'extrémité libre
- Poutre encastrée aux deux extrémités
- Poutre à travée simple avec un encastrement et un appui articulé
- Poutre à deux travées
- Poutre continue avec appui articulé - Travée interne
- Poutre continue avec appui articulé - Travée externe
Les normes suggèrent de vérifier le déversement latéral selon la méthode de la barre équivalente. Le moment critique doit être calculé avec les valeurs de rigidité à 5 %. On utilise donc les équations suivantes pour les structures bois :
Il convient de calculer la contrainte de flexion critique selon :
Si vous souhaitez considérer un ressort de rotation élastique (résultant par exemple de la flexibilité de l'appui articulé) au niveau de l'appui, un appui élastique en rotation (des bacs acier trapézoïdaux, par exemple) ou une fondation élastique de barre (par exemple, , des contreventements), vous pouvez étendre l'équation précédente comme suit : [2].
où :
Si le ressort de rotation KG de l'appui est considéré comme infiniment rigide, le résultat α = 1. Le maintien élastique en rotation KΘ n'est généralement pas considéré dans la construction bois, car il n'y a pas d'études. Ainsi, le paramètre KΘ est inclus dans l'équation avec la valeur 0. La fondation élastique de barre Ky, résultant d'un contreventement ou d'un panneau de cisaillement, a un effet favorable sur le comportement au déversement latéral d'une poutre. Il faut cependant noter que l'équation ci-dessus a une application limitée : elle n'est valide qu'en cas de flèche dans une grande courbure sinusoïdale. Si la fondation élastique de barre est trop rigide, elle n'est plus affichée car le mode propre comporte plusieurs courbures le long de la poutre. Il n’existe actuellement aucune limite à partir de laquelle la formule étendue avec α et β n'est plus valide.
Le prochain article expliquera à l'aide de différents exemples comment résoudre efficacement ce problème de valeur propre.
- Phénomène de déversement dans les structures bois | Exemples 1
- Phénomène de déversement dans les structures bois | Exemple 2