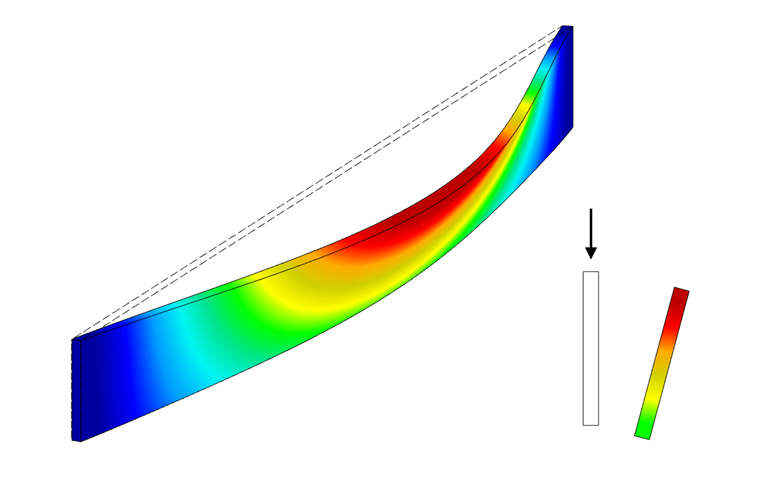
U nosníku lze pozorovat příčný posun při současném natočení (viz obr. 01). Mluvíme o prostorovém vzpěru, respektive klopení. Podobně jako u rovinného vzpěru, kdy prut při dosažení kritického Eulerova zatížení náhle vybočí, dochází při klopení k vybočení tlačené pásnice při kritickém zatížení. V průřezu vzniká kritický ohybový moment Mcrit, který vyvolává kritické ohybové napětí σcrit.
Použité symboly:
| L | Délka nosníku |
| E | modul pružnosti |
| G | Smykový modul |
| Iz | moment setrvačnosti okolo hlavní osy nejmenší tuhosti |
| IT | Moment tuhosti v prostém kroucení |
| Iω | Odolnost proti deplanaci |
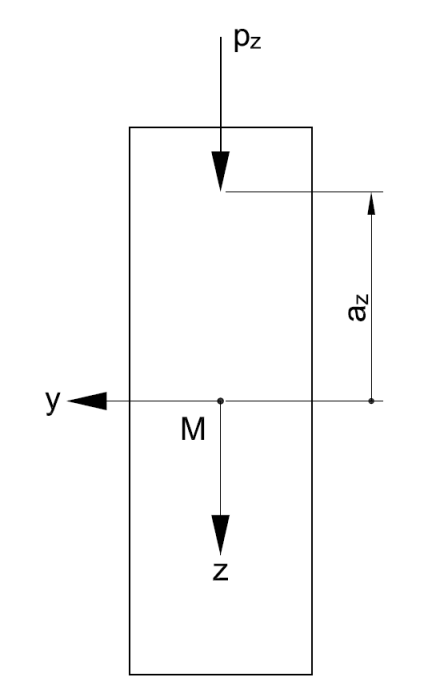
| az | vzdálenost působiště zatížení od středu smyku |
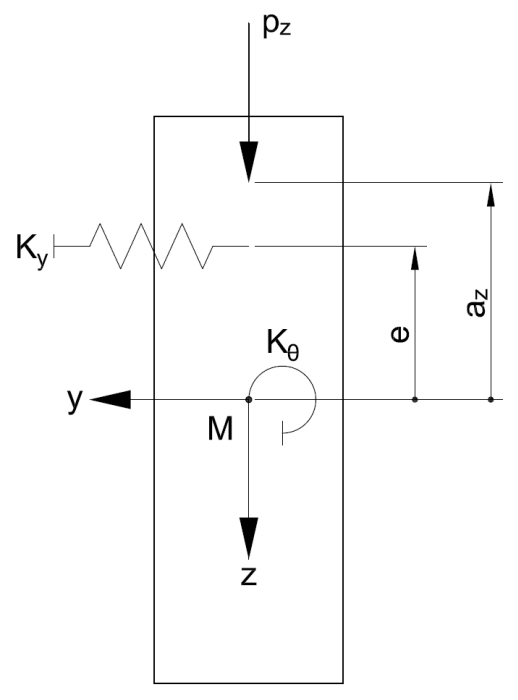
| e | vzdálenost pružného uložení prutu od středu smyku |
| KG | rotační pružina na podpoře v Nmm |
| Kθ | pružné torzní uložení v N |
| Ky | pružné podloží prutu v N/mm² |
Analytická metoda stanovení Mcrit
Pro stanovení ohybového momentu, při kterém nosník ztrácí stabilitu, nám odborná literatura nabízí analytická řešení, pro jejichž použití ovšem platí určitá omezení. V [1] je odvozena následující rovnice pro prostý nosník s oboustranným uložením proti zkroucení, s konstantním ohybovým momentem a zatížením ve středu smyku.
U průřezů bez omezení deplanace (například v případě úzkých obdélníkových průřezů v dřevěných konstrukcích) lze deplanační tuhost nastavit na nulu, a lze tak vynechat část rovnice v závorce.
Protože ve statice se setkáváme s podstatně více případy, než je ten výše popsaný, byly zavedeny korekční součinitele, kterými se například zohledňují odchylné průběhy momentů, podporové podmínky anebo působiště zatížení. Příslušnými součiniteli se přitom upraví délka nosníku a určí se účinná délka lef. V [2] je to mimo jiné popsáno následovně.
az je přitom vzdálenost působiště zatížení od středu smyku.
Pokud zatížení působí na dolní straně nosníku, pak je třeba uvažovat az se záporným znaménkem. Součinitele a1 a a2 lze převzít z obr. 03.
Rozlišujeme následující systémy:
- Prostý nosník s klouby na obou koncích a s uložením bránícím torznímu natočení
- Vetknutý nosník
- Konzola s vidlicovým uložením na volném konci
- Nosník vetknutý na obou stranách
- Prostý nosník s vetknutím na jedné straně
- Nosník o dvou polích
- Spojitý nosník s vidlicovým uložením - vnitřní pole
- Spojitý nosník s vidlicovým uložením - vnější pole
Normy navrhují provádět posouzení na klopení metodou náhradního prutu. Při výpočtu kritického momentu se uvažují hodnoty 5% kvantilu tuhosti. Pro dřevěnou konstrukci tak platí:
Kritické napětí v ohybu se tedy stanoví z výrazu:
Pokud chceme na podpoře zohlednit pružnou rotační pružinu (např. z poddajnosti vidlicového uložení), pružné torzní uložení (např. z trapézového plechu) nebo pružné uložení prutu (např. , ze ztužení), lze předchozí rovnici rozšířit následovně: [2].
kde:
Pokud je rotační pružina KG na podpoře uvažována jako nekonečně tuhá, je výsledek α = 1. Pružné torzní uložení KΘ se v dřevěných konstrukcích obecně nezohledňuje, protože neexistují žádné studie. Parametr KΘ je tak zahrnut do rovnice s hodnotou 0. Pružné podloží prutu Ky, které je výsledkem ztužení nebo smykového pole, má příznivý vliv na klopení nosníku. Je však třeba si uvědomit, že předchozí rovnice má omezené použití. Přesněji řečeno, platí pouze tehdy, pokud je průhyb ve velkém sinusovém oblouku. Pokud je podloží prutu příliš tuhé, není to již dané, protože vlastní tvar má několik oblouků podél nosníku. V současnosti neexistuje žádná definice, kdy se rozšířený vzorec s α a β stává neplatným.
Vhodné řešení vlastních čísel v takových případech ukážeme na různých příkladech v našem následujícím příspěvku.