![Analyse vibratoire (source : [3])](/fr/webimage/009798/467822/01-de-png.png)
Tout comme les structures biaxiales telles que les panneaux en lamellé croisé, la vérification est généralement effectuée sur une barre uniaxiale équivalente. Pour expliquer les principes théoriques, nous allons d'abord analyser une barre.
Exemple d'une poutre
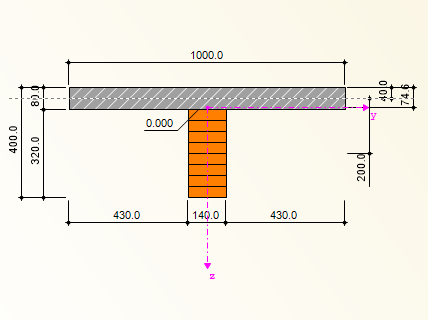
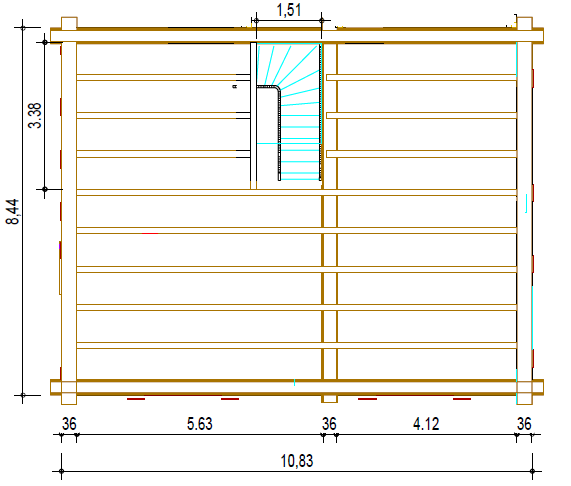
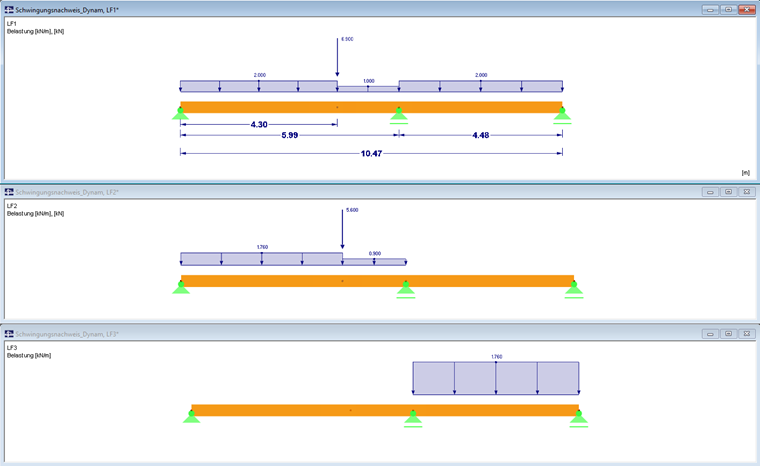
Les avantages et les inconvénients de la vérification des barres et des surfaces sont expliqués dans un composant structurel. Le plan au sol d'un bâtiment mesure 8,44 m x 10,83 m. Un mur intérieur structurel se trouve à 5,99 m dans la direction longitudinale du bâtiment. Comme le montre la Figure 02, un plancher en bois a été initialement créé et analysé dans le programme RX-TIMBER Continuous Beam. Outre les charges uniformes illustrées par la Figure 03, une charge concentrée résulte de la transition à l'extrémité de la trémie de l'escalier.
CC1 = 6,9 kN
CC2 = 5,6 kN
Le calcul effectué dans RX-TIMBER DLT permet d'obtenir une section requise de 14/32 cm.
La vérification simplifiée des vibrations dans RF-TIMBER Pro donne une déformation maximale de 19,4 mm avec la combinaison de charges CC1 + CC2. La poutre à deux travées peut être convertie en poutre encastrée à travée simple afin que les valeurs limites de déformation suivantes soient disponibles. Les vibrations sont ainsi maintenues mathématiquement sur une valeur de 8,0 Hz. Plus d'informations sont disponibles dans [3].
Une section de 14/62 cm serait nécessaire pour se conformer à l'analyse de vibration simplifiée dans RF-TIMBER Pro.
Des vérifications plus précises peuvent être effectuées dans RF-DYNAM Pro - Natural Vibrations et RF-DYNAM Pro - Forced Vibrations, en tenant compte des exigences mentionnées dans [3].
![Organigramme de [3]](/fr/webimage/009802/467834/05-de-png.png)
L'analyse détaillée vérifie d'abord si la fréquence propre est f0 ≤ fmin.
fmin = 4,5 Hz > f0 = 4,4 Hz
La limitation n'est donc pas respectée.
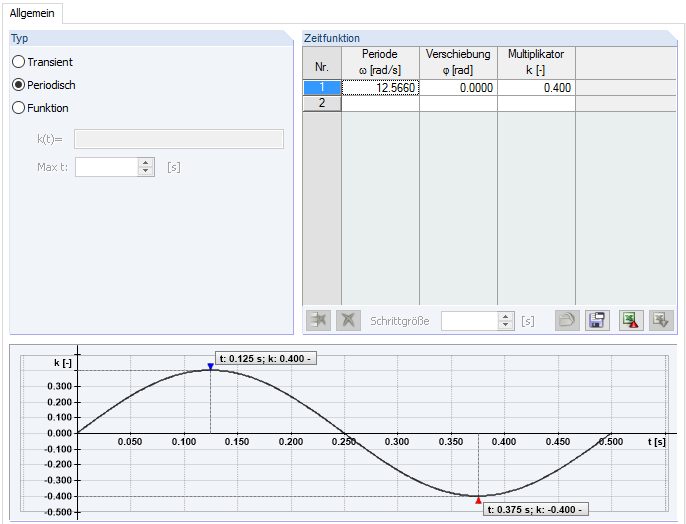
Deuxièmement, vous pouvez vérifier si l'accélération est a ≤ alim. La fonction périodique de 2 Hz est définie dans RF-DYNAM Pro - Forced Vibrations. Umgerechnet in ω mit 2Hz ∙ 2π = 12,566 rad/s. Laut [3] Abschnitt 2.2.4 kann die einwirkende Zeit-Ort-veränderliche Kraft mit Fdyn = 0,4F(t) angesetzt werden.
La définition d'une fonction périodique ne reflète pas les exigences de [3] et constitue une simplification. La représentation correcte de la marche sur un plafond est expliquée dans ce webinaire suivant:
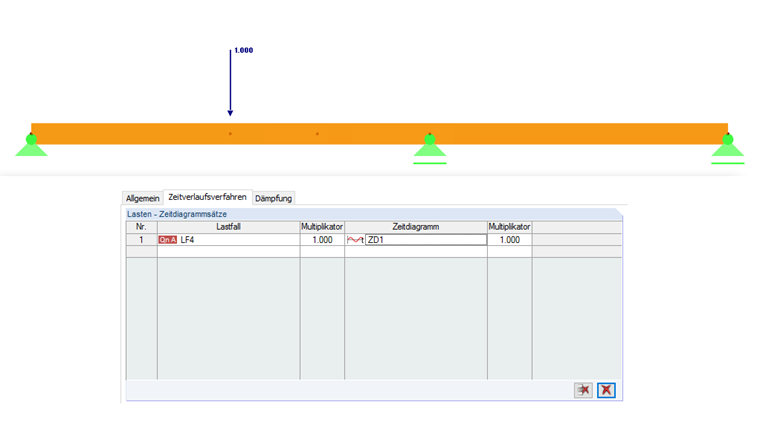
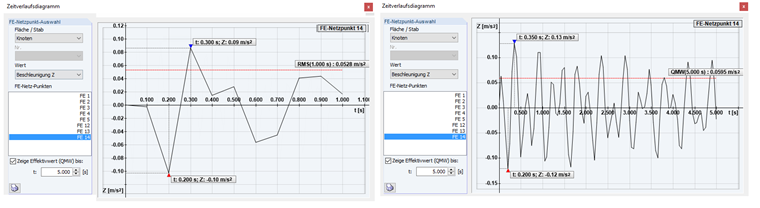
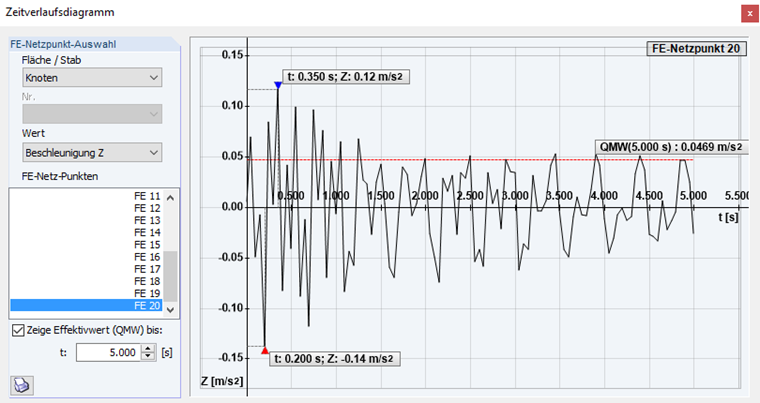
À l'étape suivante, un cas de charge est défini avec une charge concentrée de 1 kN (charge d'entretien), qui est sélectionnée pour le calcul dans RF-DYNAM Pro - Forced Vibrations. La charge concentrée est définie sur la position de la valeur propre maximale sélectionnée. Selon [1], un amortissement de Lehr's de ξ = 0,01 est utilisé. L'accélération s'étend à 2 Hz sur 5 secondes. La valeur moyenne RMS (voir la Figure 10) est calculée comme 0,05 m/s².
alimite = 0,1 m/s > a = 0,05 m/s²
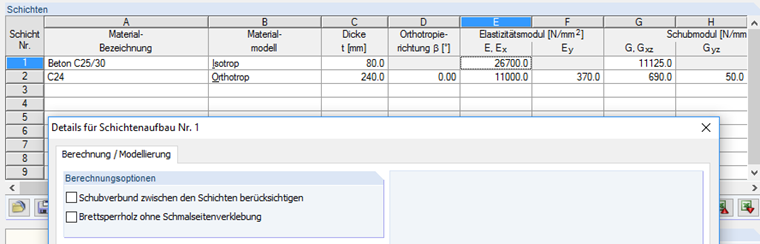
La moyenne quadratique a ainsi été vérifiée. Il en résulte cependant un léger dépassement de 0,1 m/s². Selon [3], il est possible de considérer le radier comme une rigidité et une masse supplémentaires dans le calcul. La section est définie sous les sections mixtes dans RFEM. La connexion entre la dalle et la section en bois ne transfère aucune rigidité (assemblage sans cisaillement). La hauteur de structure du radier est définie sur 8 cm. De plus amples informations sur les sections mixtes sont disponibles dans le manuel de RF-TIMBER Pro.
Exemple : Structure plane
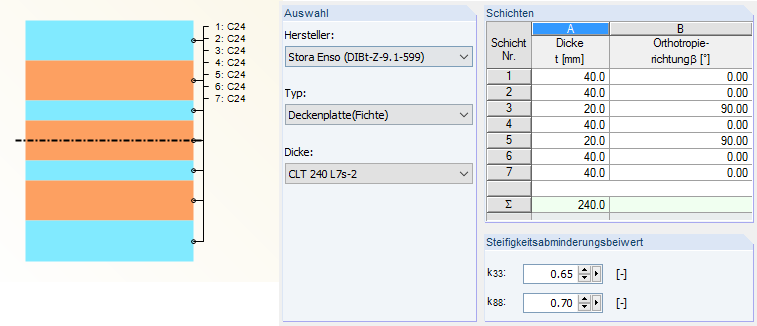
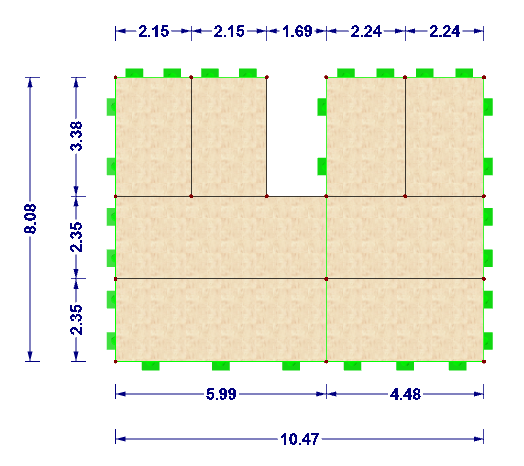
L’exemple de plan au sol représenté sur la Figure 02 a été converti en une dalle en bois lamellé-croisé avec la section CLT 240 L7a-2 (selon [2]). Les panneaux de la partie inférieure sont définis de la même manière que la structure de la poutre : la poutre continue a une longueur totale de 10,47 m et une largeur de travée de 5,99 m (travée 1) et de 4,48 m (travée 2) sont définies. Les plaques de 3,38 m de long sont connectées à des plaques continues (voir la Figure 13).
La rigidité d'assemblage des plaques n'est pas considérée dans ce cas, car on suppose que les plaques les plus courtes sont placées sur les plaques continues, il n'y a donc pas de rigidité. Lediglich für die Rotation wird an allen Plattenrändern ein Liniengelenk mit dem Freiheitsgrad φx = 0 kNm/rad/m definiert. Die Spannrichtung der Platten wird in Bild 14 erläutert.
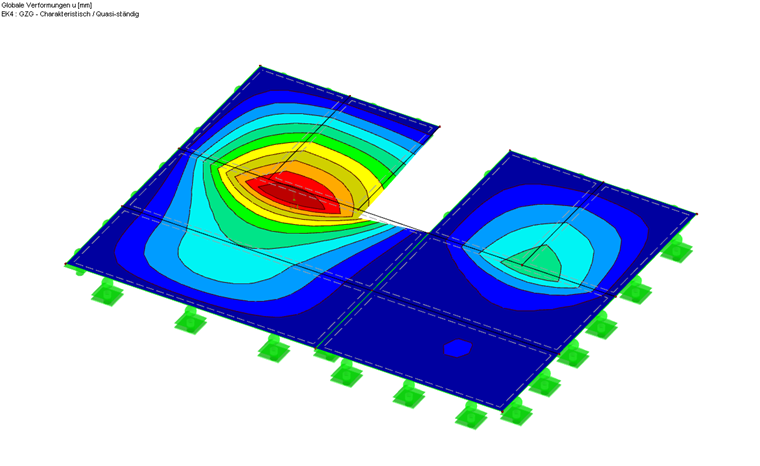
Le calcul est réalisé dans RF-LAMINATE et les rigidités calculées sont de 21,4 mm dans la combinaison caractéristique/quasi-permanente. Dans ce cas également, la vérification simplifiée des vibrations est dépassée. Par conséquent, la procédure du chapitre précédent sera répétée pour la structure plane.
Le processus de vérification dans RF-LAMINATE est expliqué dans le manuel du module additionnel RF-LAMINATE.
Afin de parvenir à un calcul plus précis de la structure de la plaque dans RF-DYNAM Pro - Natural Vibrations et RF-DYNAM Pro - Forced Vibrations, une combinaison avec CC1 + CC2 est à nouveau créée.
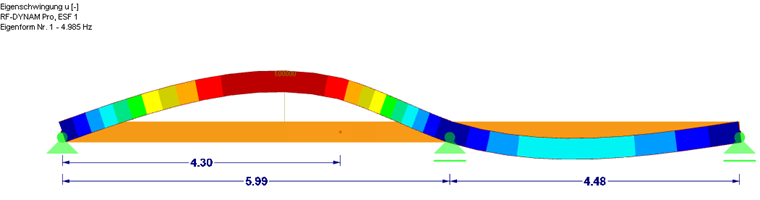
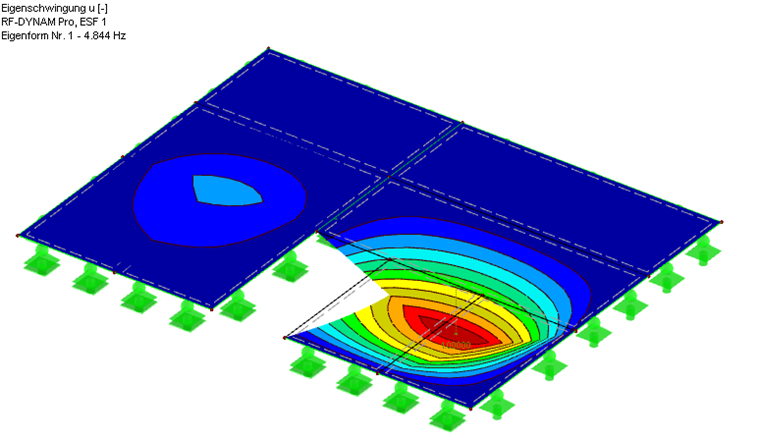
Le calcul de cette combinaison dans RF-DYNAM Pro - Natural Vibrations est une vibration propre de 4,8 Hz. Dans le premier cas, le mode de rupture maximal est également dû au milieu de la travée de la première plaque.
Dans ce cas également, la charge concentrée de 1 kN est définie et superposée avec la même fonction que dans le cas de la structure en barre. La Figure 18 montre la moyenne quadratique de 0,0469 m/s² sur 5 secondes. Selbst die maximale Beschleunigung liegt fast innerhalb des Grenzkriteriums von agrenz ≤ 0,1 m/s². La valeur limite est légèrement dépassée avec 0,12 m/s². Pour une analyse plus approfondie, la rigidité et la masse de la section seront augmentées par une chape de 8 cm d'épaisseur dans RF-LAMINATE. La rigidité de la plaque en bois lamellé-croisé est représentée par une section en bois orthotrope équivalente.
La matrice de rigidité de cette section mixte est déterminée sans considérer le couple de cisaillement entre le radier et la plaque en bois lamellé-croisé.
Grâce à cette méthode, nous avons finalement réussi à atteindre la valeur maximale de l'accélération sous le critère limite, comme vous pouvez le voir sur la Figure 20.
Conclusion
Le calcul biaxial d'un composant structurel vous permet de réduire une section de 64 cm à 22 cm d'épaisseur d'une plaque en bois lamellé-croisé tout en répondant aux vibrations selon l'Eurocode 5.