Incréments de charge pour les calculs itératifs
Il est souvent difficile d’atteindre l¤équilibre lors du calcul non-linéaire d’un système « sensible » proche de la rupture de stabilité. Notre logiciel vous permet donc d’appliquer la charge de manière incrémentale : Si deux incréments de charge sont par exemple définis, la moitié de la charge est appliquée à la première étape. Les itérations sont appliquées jusqu’à ce que l’équilibre soit atteint. Dans la deuxième étape, la charge complète est ensuite appliquée au système déjà déformé et des itérations sont effectuées jusqu’à ce que la convergence soit atteinte. Les interruptions de calcul causées par des instabilités sont ainsi évitées. Les calculs réalisés à l'aide d’incréments de charge prolongent systématiquement le temps de calcul. Vous pouvez définir des incréments de charge globaux ou spécifiques à certains cas de charge et certaines combinaisons de charges.
RFEM vous permet également d’enregistrer les résultats d’incréments de charge individuels lors des calculs. Sélectionnez le paramètre souhaité dans la boîte de dialogue « Paramètres de calcul » du cas de charge ou de la combinaison de charges. Les diagrammes des efforts et des moments sont par exemple affichés avec les effets non-linéaires, ce qui peut générer des redistributions distinctes sur le modèle.
Cet article traite trois exemples simples de calculs itératifs, qui illustrent l’évolution progressive des résultats en fonction de niveaux de charge croissants.
Ressort avec limites
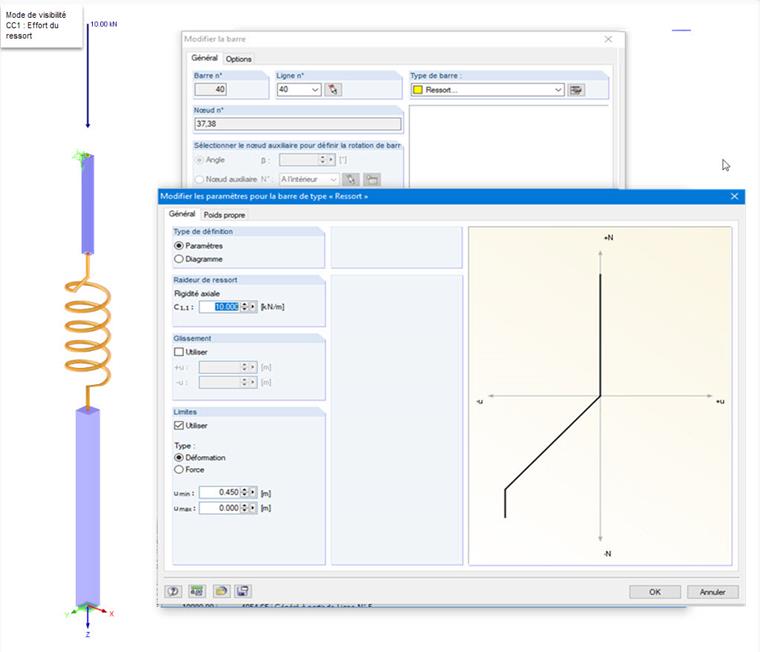
Une barre télescopique comprimée est représentée par deux tubes et leurs déplacements sont contrôlés par un ressort, qui joue le rôle d’élément intermédiaire. La rigidité axiale du ressort et les limites de déformation ou de l’effort peuvent être renseignées dans la boîte de dialogue « Modifier les paramètres du type de barre Ressort ». Dans l’exemple traité ici, la force de compression n’est plus compensée une fois qu’un raccourcissement de 45 cm a été atteint.
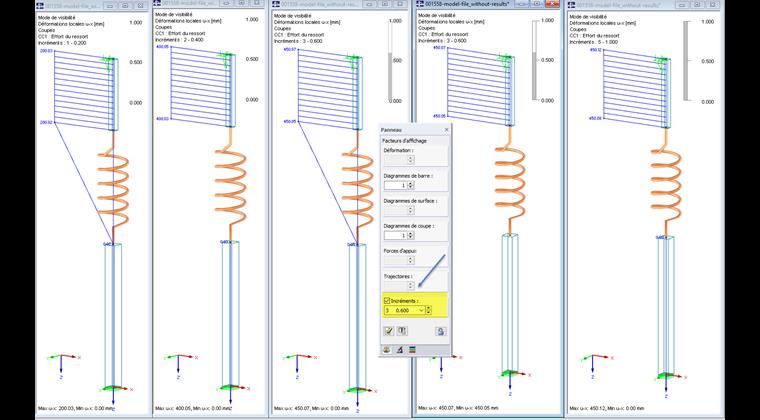
La charge nodale est appliquée en cinq incréments de charge. Le calcul est effectué selon l’analyse statique linéaire. La déformation du ressort de 20 cm et 40 cm se trouve dans l’espace de travail actif avec 20 % et 40 % de la charge. La barre supérieure est déplacée vers le bas en conséquence. Si la charge est augmentée à 60 %, 80 % et enfin 100 %, la déformation n’augmente plus avec une flèche de ressort de plus de 45 cm. La déformation de la barre supérieure demeure constante. Les légères différences de décimales sont dues au raccourcissement des tubes.
Portique avec diagonales dont l’effort normal est limité et appuis avec glissement
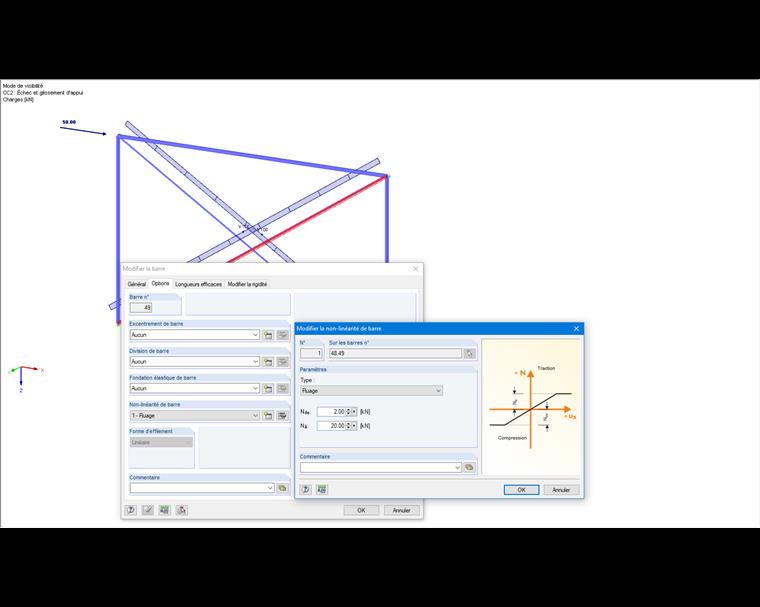
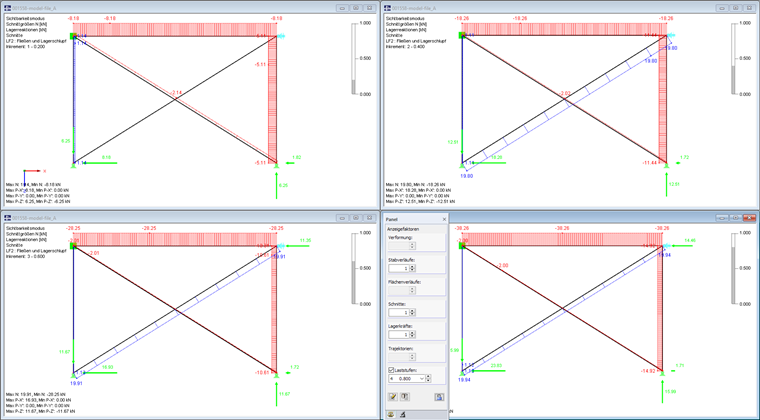
Un portique est stabilisé par des contreventement diagonaux entrecroisés. La résistance axiale des sections en L précontraintes est contrôlée par un critère d’élasticité. Seuls les efforts de traction de 20 kN au maximum et les forces compression de 2 kN au maximum peuvent être absorbés. Les forces et les efforts hors de cet intervalle augmentent la déformation sans absorber d’efforts ou de forces supplémentaires.
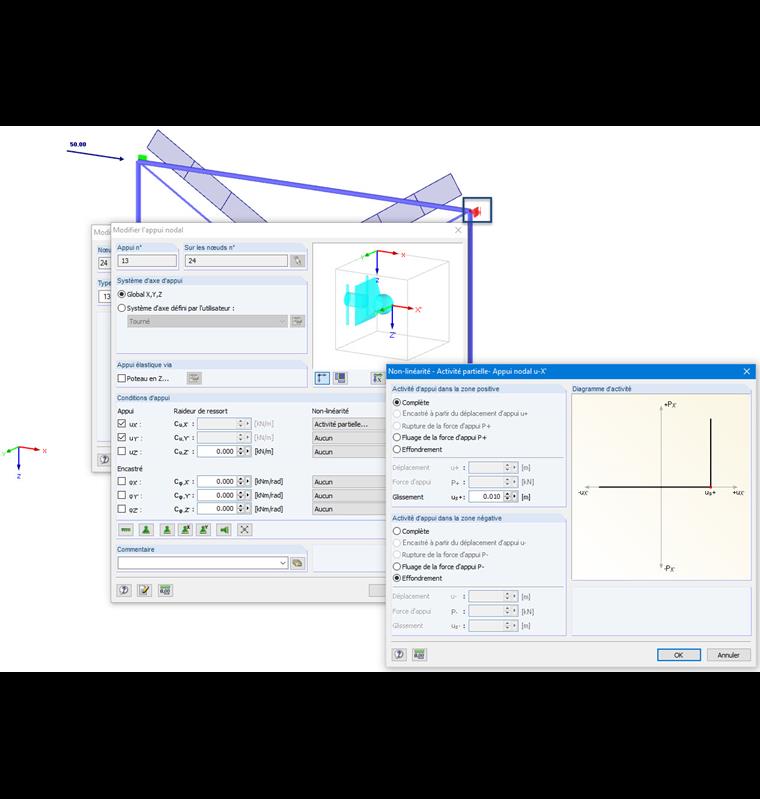
De plus, un appui horizontal agissant de manière non linéaire avec glissement est défini sur un assemblage de portique représentant un voile adjacent. Il agit uniquement sur les forces de compression dès qu’un déplacement nodal horizontal d’un centimètre se produit.
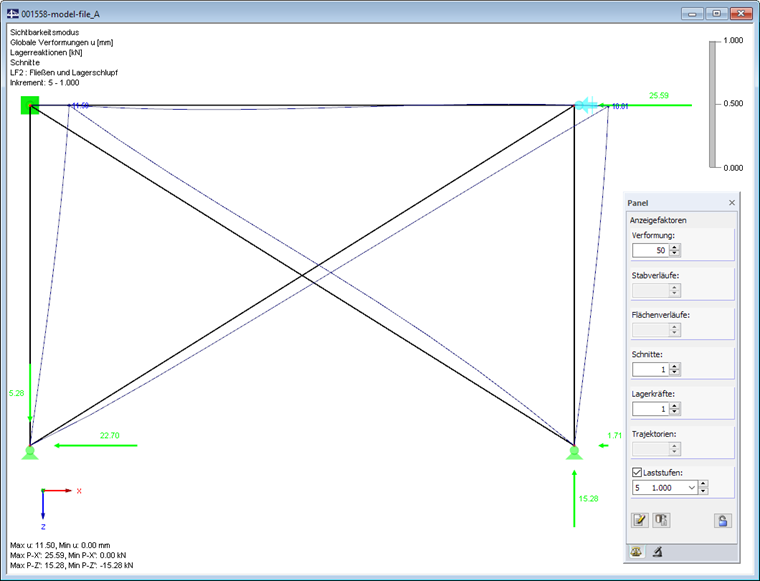
La charge nodale est à nouveau appliquée en cinq incréments de charge. Les calculs sont effectués selon l’analyse du second ordre. Si le niveau de charge s’élève à 20 %, une diagonale suffit pour transférer la charge nodale comme force de compression dans le système. Si le niveau de charge s’élève à 40 %, un effort de traction s’exerce également sur la seconde diagonale. On peut déjà constater le comportement de fluage de ces deux diagonales. Elles suffisent cependant à stabiliser le système sans appui horizontal. Cet appui agit uniquement à partir d’un niveau de charge de 60 %.
Les effets de redistribution sont finis dans les autres incréments de charge. Une déformation totale de 10,01 mm se produit au niveau du nœud désormais supporté dans l’assemblage de portique (prenant en compte le ratio Z).
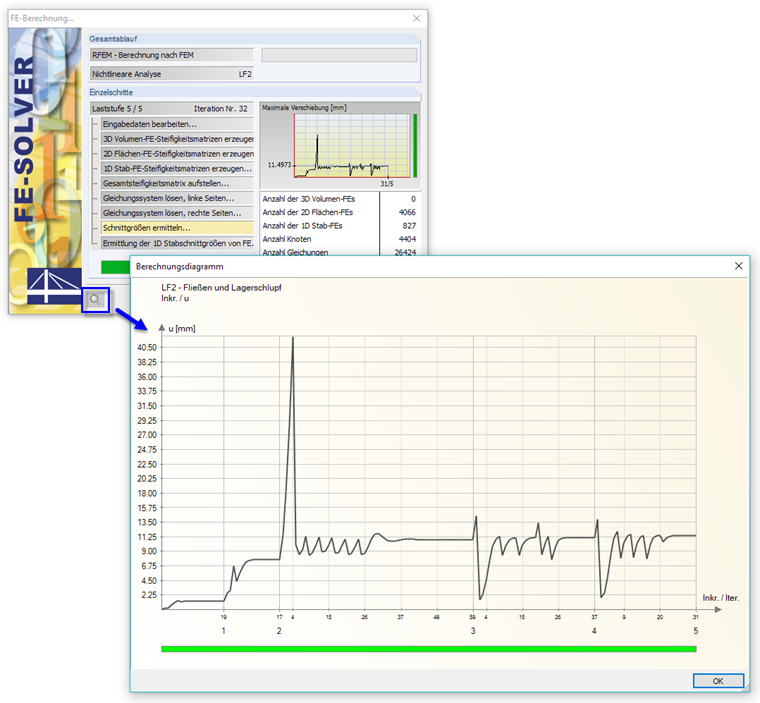
La distribution des déformations (par défaut) dans chaque incrément de charge est affichée sous forme de diagramme lors du calcul. La barre sous le diagramme est verte si les déformations se situent dans l’intervalle admissible. Une barre rouge signifie, dans la plupart des cas, que certaines rotations sont trop grandes (rayon égal ou supérieur à 0,1 rad). Vous pouvez afficher et évaluer les diagrammes de calcul une fois le calcul terminé en accédant à la boîte de dialogue « Paramètres de calcul », onglet « Diagrammes de calcul ».
Assemblage de portique avec comportement plastique des matériaux
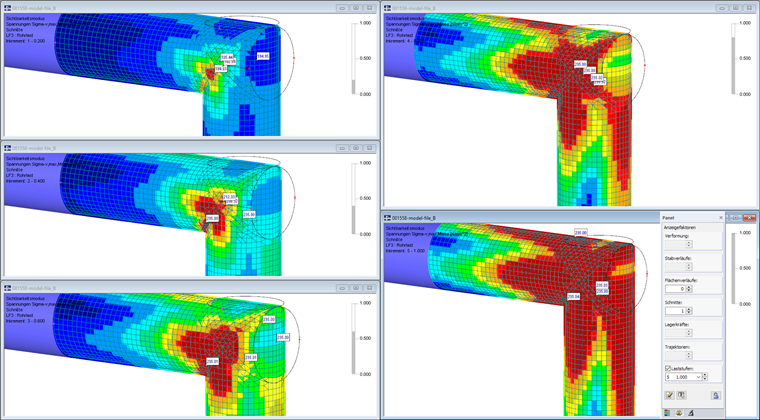
Une charge verticale est appliquée sur un portique tubulaire en acier. Cette zone est modélisée à l’aide d’intersections surfaciques pour effectuer l’analyse plastique de l’assemblage de portique. Les surfaces présentent un comportement de matériau isotrope plastique : la contrainte ne peut plus augmenter au-delà de la limite d’élasticité de 235 N/mm².
Le module additionnel RF-MAT NL est nécessaire pour analyser le comportement des matériaux non-linéaires. Cinq incréments de charge sont à nouveau appliqués. Les résultats des contraintes équivalentes montrent l’évolution de la plastification pour chaque niveau de charge. La distribution des efforts internes « Constante aux éléments » doit être sélectionnée (voir également l’article sur les options de lissage) pour évaluer l’analyse plastique.
Conclusion
Cet article traite des exemples simples pour calculer avec des incréments de charge. Cette méthode est généralement adaptée aux systèmes sensibles ou pour la considération de grandes déformations. Elle peut également être utilisée pour des analyses spécifiques du comportement structurel en prenant en compte la redistribution ou les effets non-linéaires.
Le nombre d’itérations doit être suffisamment élevé pour effectuer des calculs non-linéaires. Si aucune convergence n’est atteinte au seuil des limites définies, un message correspondant apparait une fois le calcul terminé. Vous pouvez ensuite consulter les résultats de l’analyse incomplète pour identifier d’éventuels problèmes ou ajuster les paramètres de calcul.
Les graphiques de résultat de chaque incrément de charge peuvent être documentés dans le rapport d’impression et ainsi utilisés pour approfondir le calcul de la structure.