Přírůstky zatížení pro iterační výpočet
Při nelineárním výpočtu systému náchylného ke ztrátě stability je často obtížné dosáhnout rovnováhy. Proto program nabízí možnost navyšovat zatížení konstrukce postupně v několika krocích: Pokud například zadáme dva přírůstky zatížení, zatíží se konstrukce v prvním kroku pouze poloviční hodnotou zatížení. Následně proběhne iterační výpočet až do dosažení rovnováhy. V druhém kroku se na již přetvořenou konstrukci vloží celkové zatížení a znovu se provede iterační výpočet až do dosažení rovnováhy. Tímto způsobem se můžeme vyhnout přerušení výpočtu z důvodu nestability. Výpočet s přírůstky zatížení nutně prodlužuje dobu výpočtu. Počet přírůstků zatížení lze nastavit jak globálně, tak jednotlivě pro konkrétní zatěžovací stavy a kombinace zatěžovacích stavů.
RFEM také umožňuje ukládat během výpočtu výsledky jednotlivých přírůstků zatížení. Přírůstky zatížení se nastavují v záložce „Parametry výpočtu“ vybraného zatěžovacího stavu nebo kombinace zatížení. Lze tak například vysledovat, jaký vliv mají na průběhy sil a momentů nelineární účinky, které mohou vést k výrazné redistribuci v modelu.
V tomto článku představíme tři jednoduché příklady iteračních výpočtů, na nichž lze dobře pozorovat, jak se mění výsledky při postupně se zvyšujícím zatížení.
Pružina se zastavením
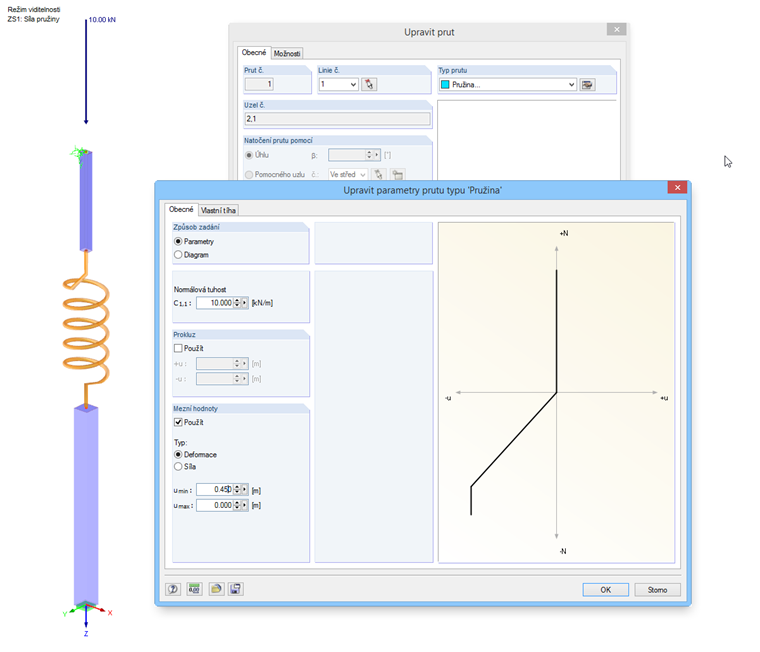
Teleskopický prut namáhaný v tlaku modelujeme pomocí dvou trubek, mezi které je pro regulaci posunu zařazena pružina. Osovou tuhost pružiny a omezení deformace nebo síly lze stanovit v dialogu „Upravit parametry prutu typu 'Pružina'“. V našem příkladu již nedochází ke kompenzaci tlakové síly, jakmile je dosaženo stlačení 45 cm.
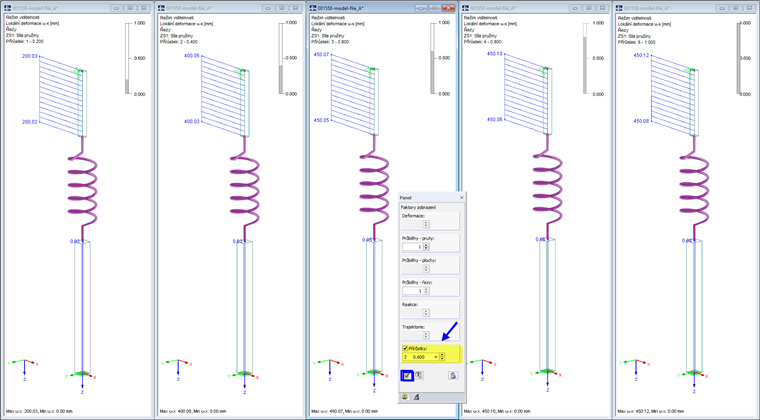
Uzlové zatížení se bude navyšovat v 5 krocích. Při statickém výpočtu se uplatní lineární analýza. Deformace pružiny činí 20 cm při uvážení 20 % zatížení a 40 cm v případě 40 % zatížení, a nachází se v účinné oblasti pracovního diagramu. Horní prut se úměrně posouvá dolů. Jestliže se zatížení zvýší na 60 %, 80 % a nakonec 100 %, deformace se po stlačení pružiny o 45 cm již nezvětšuje. Deformace horního prutu se nemění. Minimální rozdíly v desetinných číslech jsou způsobeny stlačením trubek.
Rám s omezením osových sil v diagonálách a s podepřením s prokluzem
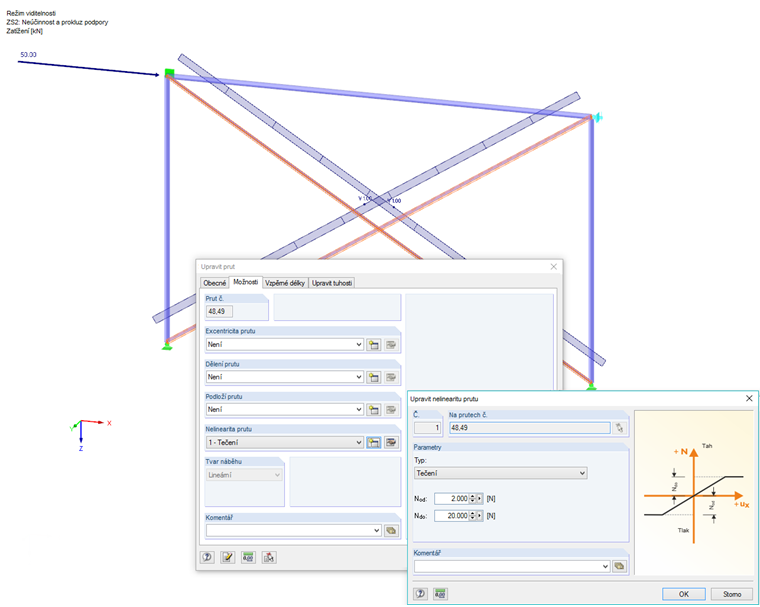
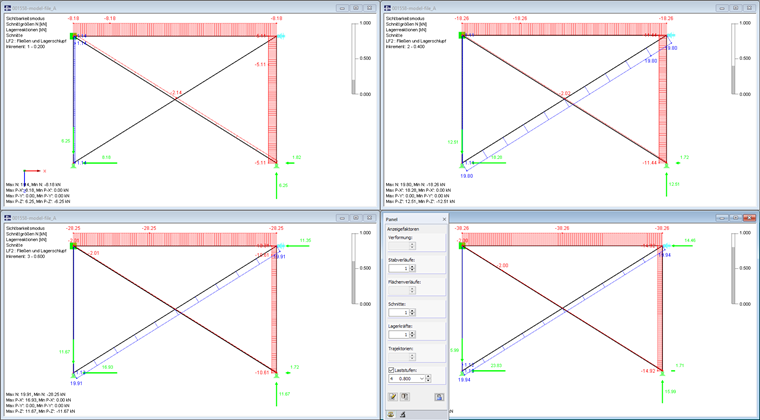
Rám má diagonální ztužení. Pro osovou únosnost předpjatých L-profilů je definována podmínka plasticity: Přenáší se pouze tlak do 2 kN a tah do 20 kN. Síly mimo tento rozsah zvyšují přetvoření, aniž by byly přenášeny.
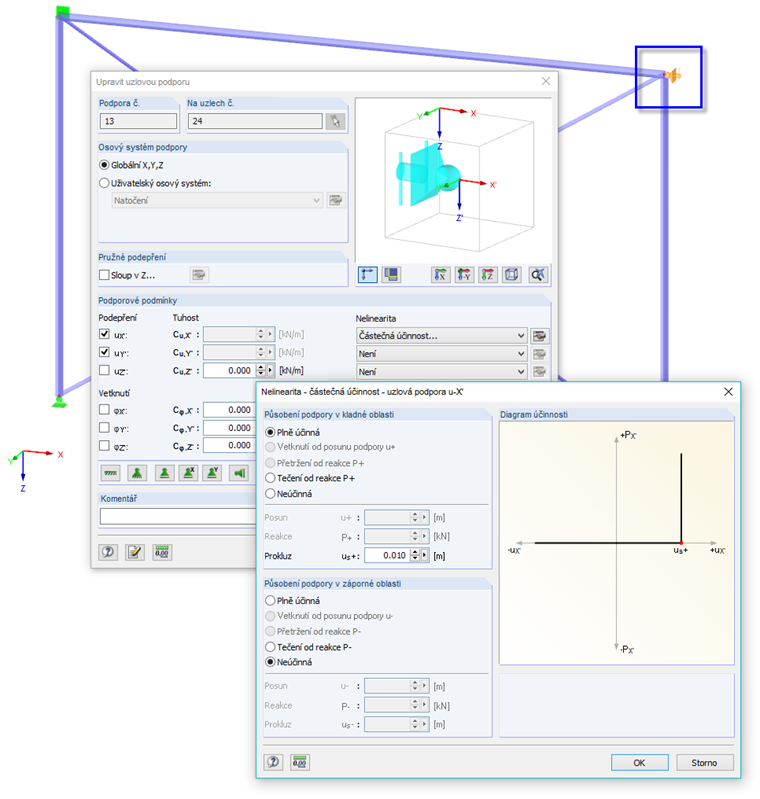
Dále zadáme nelineární vodorovnou podporu s prokluzem na jednom rámovém rohu, pomocí níž modelujeme sousední stěnu. Je účinná pouze v tlaku po dosažení vodorovného posunu v uzlu o 1 cm.
Uzlové zatížení se bude navyšovat v 5 krocích. Výpočet provedeme podle teorie druhého řádu. Při 20 % zatížení stačí jediná diagonála k přenosu uzlového zatížení jako tlakové síly do systému. Při 40 % zatížení navíc v druhé diagonále vzniká tahová síla. U obou diagonál se již projevuje plastizace. Tyto diagonály ovšem stačí ke stabilizaci konstrukce bez vodorovné podpory. Podpora je účinná teprve od 60 % zatížení.
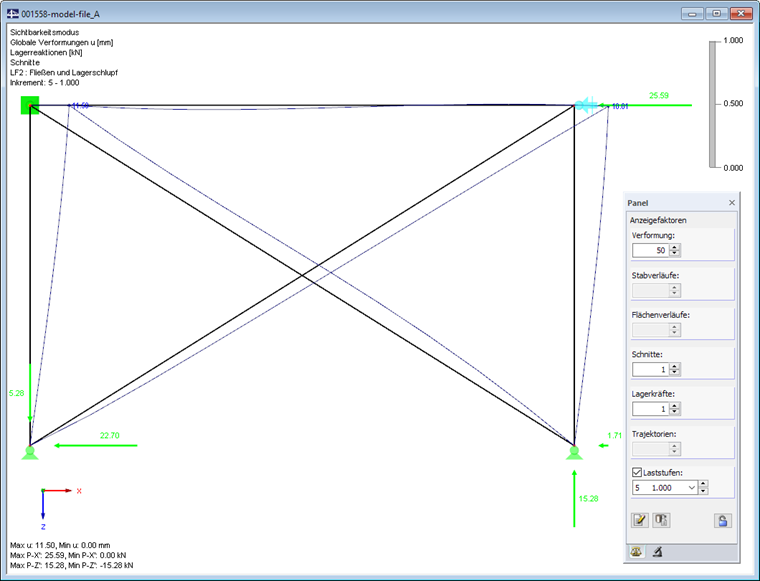
Při dalším zvyšování zatížení již redistribuce neprobíhá. Na nyní již podepřeném uzlu v rámovém rohu lze (při zohlednění složky Z) zaznamenat celkovou deformaci 10,01 mm.
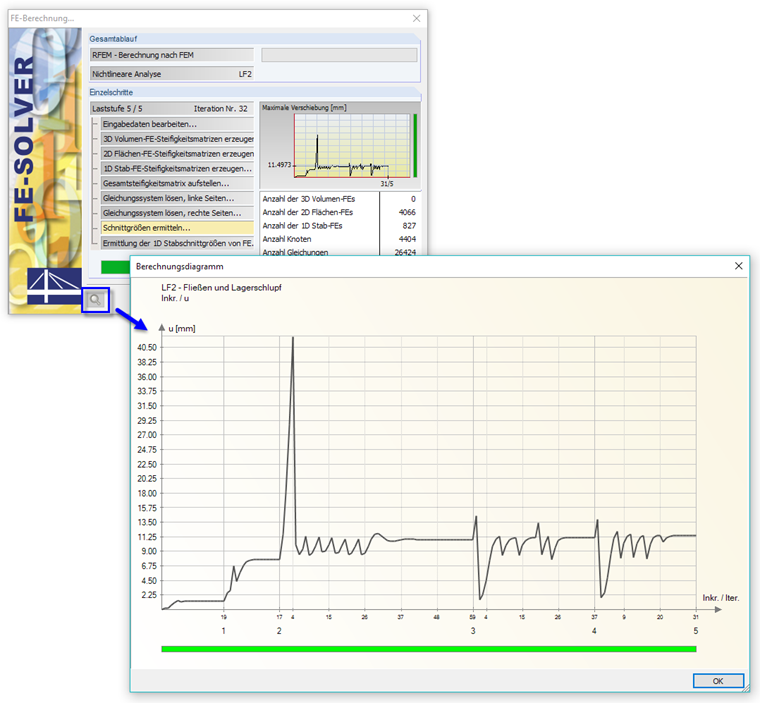
Při výpočtu se průběh deformací v jednotlivých zatěžovacích krocích standardně zobrazí v diagramu. Pokud jsou deformace v přípustné oblasti, je pruh zelený. Červený pruh obvykle znamená příliš velké natočení (≥ 0,1 rad). Výpočtové diagramy jsou k dispozici také po výpočtu v dialogu „Parametry výpočtu“ v záložce „Výpočtový diagram“ pro podrobné vyhodnocení.
Rámový roh s plastickým chováním materiálu
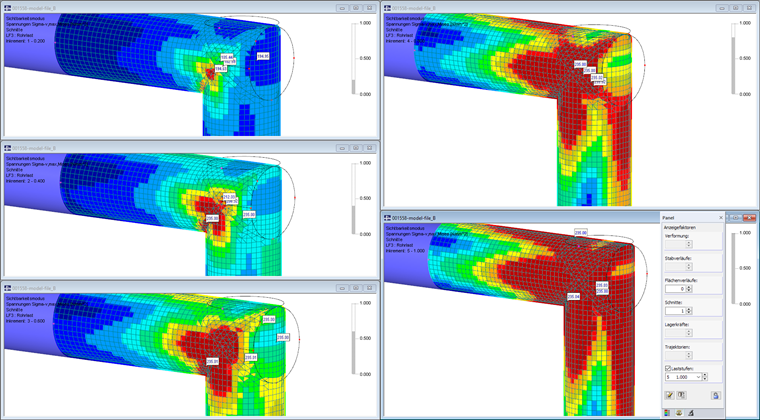
Rám z ocelových trubek je namáhán svislým zatížením. Pro plastickou analýzu rámového rohu modelujeme tuto oblast pomocí průniků ploch. Plochy vykazují izotropní plastické chování: Po dosažení napětí na mezi kluzu 235 N/mm² se již nemůže napětí nadále zvyšovat.
Analýza nelineárního chování materiálu vyžaduje přídavný modul RF-MAT NL. Zatížení budeme opět navyšovat v 5 krocích. Z výsledných srovnávacích napětí je zřejmé, jak postupuje plastizace v jednotlivých zatěžovacích krocích. Pro vyhodnocení plastické analýzy bychom měli zvolit průběh napětí „Konstantní v prvcích“ (viz také Databáze znalostí: Možnosti vyhlazení).
Shrnutí
V našem příspěvku jsme ukázali několik jednoduchých příkladů výpočtu s přírůstky zatížení. Tento postup je v zásadě vhodné použít u systémů náchylných ke ztrátě stability nebo pro zohlednění velkých deformací, dále také při cílené analýze chování nosné konstrukce se zřetelem k redistribuci sil nebo k nelineárním účinkům.
U nelineárních výpočtů je třeba zvolit dostatečně vysoký počet možných iterací. Pokud není v rámci stanoveného limitu dosažena konvergence, zobrazí se po skončení výpočtu příslušné hlášení. Výsledky nedokončené analýzy si následně můžeme prohlédnout, abychom mohli stanovit problematické oblasti anebo upravit výpočetní parametry.
Grafická znázornění výsledků pro jednotlivé přírůstky zatížení můžeme zařadit do výstupního protokolu a díky nim přehledně zdokumentovat průběh statické analýzy.